1. Propiedad molar parcial en soluciones binarias
Anuncio

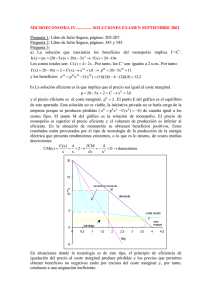
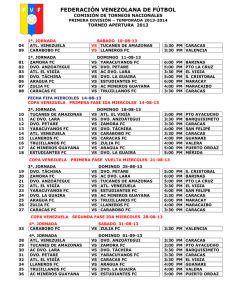
Termodinámica del equilibrio Profesor: Alı́ Gabriel Lara Propiedad molar parcial (Cont.) 1. Propiedad molar parcial en soluciones binarias Forma gráfica Si el sistema fuera binario y considerando que disponemos datos experimentales entonces para una propiedad termodinámica arbitraria M ( ) ∂M M1 = M − (1) x2 ∂x2 T,P ( ) ∂M M2 = M − x1 (2) ∂x1 T,P Claro como la datos experimentales que se disponen en soluciones binarias están graficadas en función de uno de los componentes, las ecuaciones (1) y (2) pueden ser reescritas, utilizando el hecho que x1 + x2 = 1 y por tanto dx1 = −dx2 . Resultando que para la propiedad arbitraria M en un proceso a T y P constante. dM dx1 dM M 2 = M − x1 dx1 M 1 = M + x2 (3) (4) Entonces con un gráfico donde se presente la variación de una propiedad M arbitraria en función de x1 , tenemos que; dM → pendiente de la tangente dx1 Dicha pendiente la podemos expresar a partir de la geometrı́a del triángulo rojo y azul descrito en la figura adyacente de la siguiente manera: dM I1 − I2 M − I2 = ≡ dx1 1 x1 TANGENTE EN X 1 I1 M I2 0 x1 1 Es decir; [ ] dM dM 1 dM I2 = I1 − ⇒ = M − I1 + dx1 dx1 x1 dx1 Reordenando; x1 dM dM dM = M − I1 + → I1 = M + (1 − x1 ) dx1 dx1 dx1 dM ⇒ I1 = M + x2 = M1 dx1 1 (5) Por otra parte, se puede deducir que; I2 = M − x1 dM = M2 dx1 (6) Entonces, del gráfico se puede leer directamente las propiedades molares parciales de cada uno de los = 1 componentes al conocer el corte de la tangente a la curva de la propiedad de la mezcla evaluada a la ∞ M = M 1 = I1 1 composicin de interés con los ejes. 2 = 2 También a partir del mismo gráfico podemos co∞ nocer el valor de M i . Es decir, la propiedad parcial M2 = M 2 = I2 molar del componente 1 a dilución infinita. Por di0 1 x1 lución infinita se entiende cuando x1 → 0, entonces para estimar el valor de la propiedad a esta condición lo que se hace es pasar la tangente a la curva de la propiedad de la mezcla cuando x1 = 0 tal como se muestra en el gráfico de la izquierda. M M ∞ 1 M M 2. Propiedad cambio de mezclado El hecho de que las propiedades molares parciales de cada especie en una mezcla sean diferentes de las propiedades molares de los componentes puros, provoca cambios en la propiedades termodinámicas durante el proceso de formación de una mezcla a partir de componentes puros. Por ejemplo, si consideramos una mezcla a partir de n1 moles de la especie 1, n2 moles de la especie 2, etc. El volumen total y la entalpı́a de los componentes puros NO MEZCLADOS son; V = H= C ∑ i C ∑ ni Vi (T, P ) ni Hi (T, P ) i mientras que el volumen y la entalpa de la mezcla a la misma T y P son; V (T, P, n1 , n2 , . . .) = nV (T, P, x1 , x2 , . . .) = H(T, P, n1 , n2 , . . .) = nV (T, P, x1 , x2 , . . .) = C ∑ i C ∑ ni V i (T, P, x1 , x2 , . . .) ni H i (T, P, x1 , x2 , . . .) i Por consiguiente, el cambio isotérmico de volumen en la mezcla ∆Vm y el cambio isotérmico de 2 entalpa en la mezcla o el calor de mezclado, ∆Hm , son: ∆Vm (T, P, n1 , n2 , . . .) = V (T, P, n1 , n2 , . . .) − C ∑ ni Vi (T, P ) i = C ∑ [ ] ni V i (T, P, x1 , x2 , . . .) − Vi (T, P ) i ∆Hm (T, P, n1 , n2 , . . .) = H(T, P, n1 , n2 , . . .) − C ∑ ni Vi (T, P ) i = C ∑ [ ] ni H i (T, P, x1 , x2 , . . .) − Hi (T, P ) i Se puede definir de manera similar otras propiedades de cambio de mezclado con las otras propiedades termodinámicas a presión, temperatura y composición constantes. Es decir, para un propiedad termodinámica M , escrita en forma intensiva; [ ] ∑ M= xi Mi + ∆Mm (7) T,P donde M : Propiedad molar de la mezcla Mi : Propiedad del componente puro ∆Mm : Es la propiedad de cambio de mezclado. Puede ser positivo o negativo ∑ Sabiendo que por Euler M = xi M i , entonces; ∑ ∑ ∆Mm = xi M i − xi Mi Ahora si decimos que: ∑ ( ) x i H i − Hi ∑ ( ) ∆Vm = xi V i − Vi ∑ ( ) ∆Gm = xi Gi − Gi M = H ⇒∆Hm = 3 (8)