Primer Práctica Dirigida

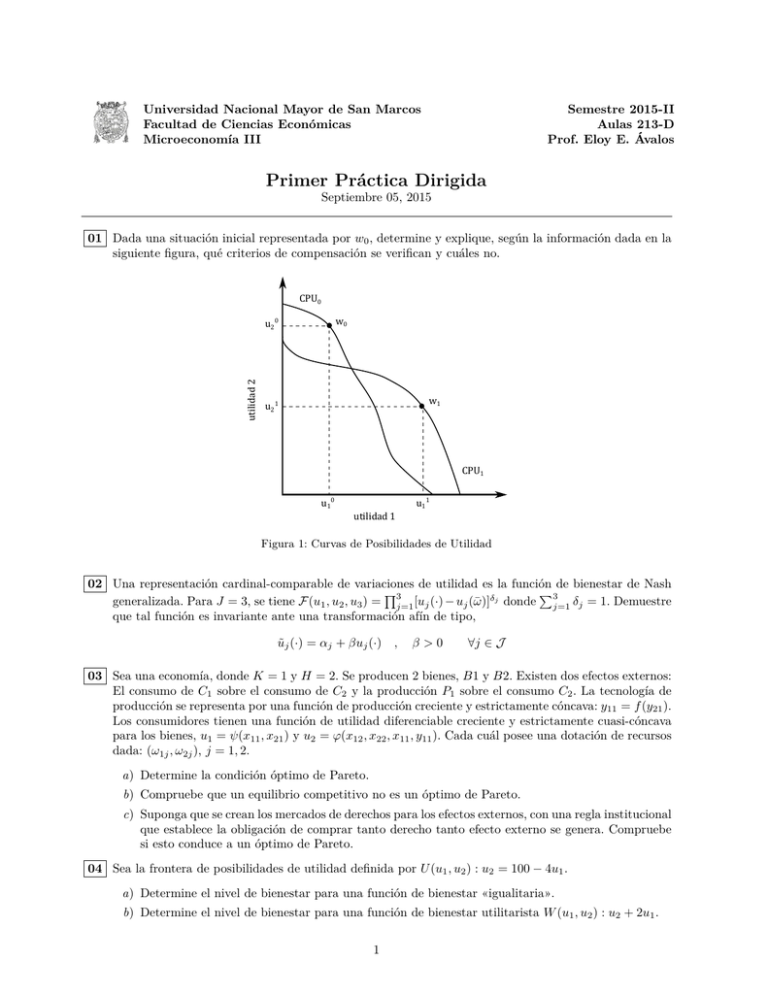
Universidad Nacional Mayor de San Marcos
Facultad de Ciencias Económicas
Microeconomía III
Semestre 2015-II
Aulas 213-D
Prof. Eloy E. Ávalos
Primer Práctica Dirigida
Septiembre 05, 2015
01 Dada una situación inicial representada por w0 , determine y explique, según la información dada en la
siguiente figura, qué criterios de compensación se verifican y cuáles no.
CPU0
w0
utilidad2
u2 0
w1
u2 1
CPU1
u1 0
u1 1
utilidad1
Figura 1: Curvas de Posibilidades de Utilidad
02 Una representación cardinal-comparable de variaciones de utilidad es la función de bienestar de Nash
Q3
P3
generalizada. Para J = 3, se tiene F(u1 , u2 , u3 ) = j=1 [uj (·) − uj (ω̄)]δj donde j=1 δj = 1. Demuestre
que tal función es invariante ante una transformación afín de tipo,
ũj (·) = αj + βuj (·) ,
β>0
∀j ∈ J
03 Sea una economía, donde K = 1 y H = 2. Se producen 2 bienes, B1 y B2. Existen dos efectos externos:
El consumo de C1 sobre el consumo de C2 y la producción P1 sobre el consumo C2 . La tecnología de
producción se representa por una función de producción creciente y estrictamente cóncava: y11 = f (y21 ).
Los consumidores tienen una función de utilidad diferenciable creciente y estrictamente cuasi-cóncava
para los bienes, u1 = ψ(x11 , x21 ) y u2 = ϕ(x12 , x22 , x11 , y11 ). Cada cuál posee una dotación de recursos
dada: (ω1j , ω2j ), j = 1, 2.
a) Determine la condición óptimo de Pareto.
b) Compruebe que un equilibrio competitivo no es un óptimo de Pareto.
c) Suponga que se crean los mercados de derechos para los efectos externos, con una regla institucional
que establece la obligación de comprar tanto derecho tanto efecto externo se genera. Compruebe
si esto conduce a un óptimo de Pareto.
04 Sea la frontera de posibilidades de utilidad definida por U (u1 , u2 ) : u2 = 100 − 4u1 .
a) Determine el nivel de bienestar para una función de bienestar «igualitaria».
b) Determine el nivel de bienestar para una función de bienestar utilitarista W (u1 , u2 ) : u2 + 2u1 .
1
c) Determine el nivel de bienestar para una función de bienestar rawlsiana W (u1 , u2 ) = mı́n[4u1 , u2 ].
d) Determine el nivel de bienestar para una función de bienestar de Nash W (u1 , u2 ) = (u1 −5)(u2 −10).
e) Determine cuál de las tres funciones de bienestar es más próxima al resultado «igualitario». Represente gráficamente.
2