Analogías Electro
Anuncio

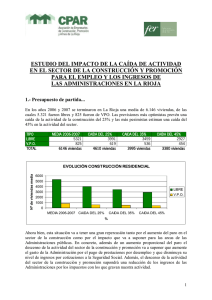
1 José Luis Rodríguez, Ph.D., Junio de 2005 Analogías Electro-Mecánicas Definición de Variables Potencial y Flujo SISTEMA Cantidad Fundamental Variable Potencial Variable Flujo Eléctrico carga eléctrica voltaje corriente Hidráulico volumen presión flujo Neumático masa presión flujo Térmico energía interna temperatura calor Mecánico Lineal posición lineal fuerza velocidad lineal Mecánico Rotacional posición angular torque velocidad angular Relaciones Fundamentales en Sistemas Electro-Mecánicos SISTEMA Cantidad Fundamental Variable Potencial Variable Flujo Caida de potencial en una resistencia Caida de potencial en una inductancia Caida de potencial en una capacitancia Eléctrico q V dq i= dt dq VR = Ri = R dt d2 q di VL = L = L 2 dt dt 1 Rt 1 q VC = i (τ ) dτ = C 0 C Mecánico Lineal x F dx V = dt dx FR = BV = B dt d2 x dV =m 2 FL = m dt dt Mecánico Rotacional θ T dθ ω= dt dθ TR = Bω = B dt d2 θ dω =m 2 TL = J dt dt FC = Kx TC = Kθ Leyes Eléctricas: 1) La sumatoria algebraica de las corrientes en un nodo es igual a cero. 2) La caida de potencial en una rama es igual al voltaje aplicado. Leyes Mecánicas: La sumatoria de fuerzas es igual al producto de la masa por la aceleración del cuerpo. Analogías Electro-Mecánicas Imp. Electricas Inductancia Resistencia Capacitancia Corriente Carga Voltaje Ls2 Rs 1 C I (s) = sQ (s) Q (s) V (s) Imp. Mecanicas Rectilíneas Ms2 Bs Imp. Mecanicas Rotacionales Js2 Bs K K V (s) = sX (s) X (s) F (s) ω (s) = sθ (s) θ (s) T (s) Nota: Al aplicar el teorema de las mallas para resolver el circuito, la malla se resuelve en términos de carga, Q (s) , o posición: X (s) o θ (s) ; y no en términos de corriente, I (s) , o velocidad: V (s) o ω (s) como es hecho usualmente.