MATEMÁTICA DISCRETA
Producto Académico Nº 3
Foro de debate
Nombre: JOEL HUGO CONDORI PANCA
1. PROPOSITO DEL FORO
Los foros virtuales representan una solución de encuentro a través de medios electrónicos
en situaciones en las que los participantes no pueden reunirse personalmente y que los
proyectos permiten debates asíncronos. Los objetivos de un foro virtual están orientados a
debatir sobre situaciones problematizadoras, resolver problemas, crear ideas, distribuir
conocimiento y/o desarrollar buenas prácticas.
2. INSTRUCCIONES
Descripción
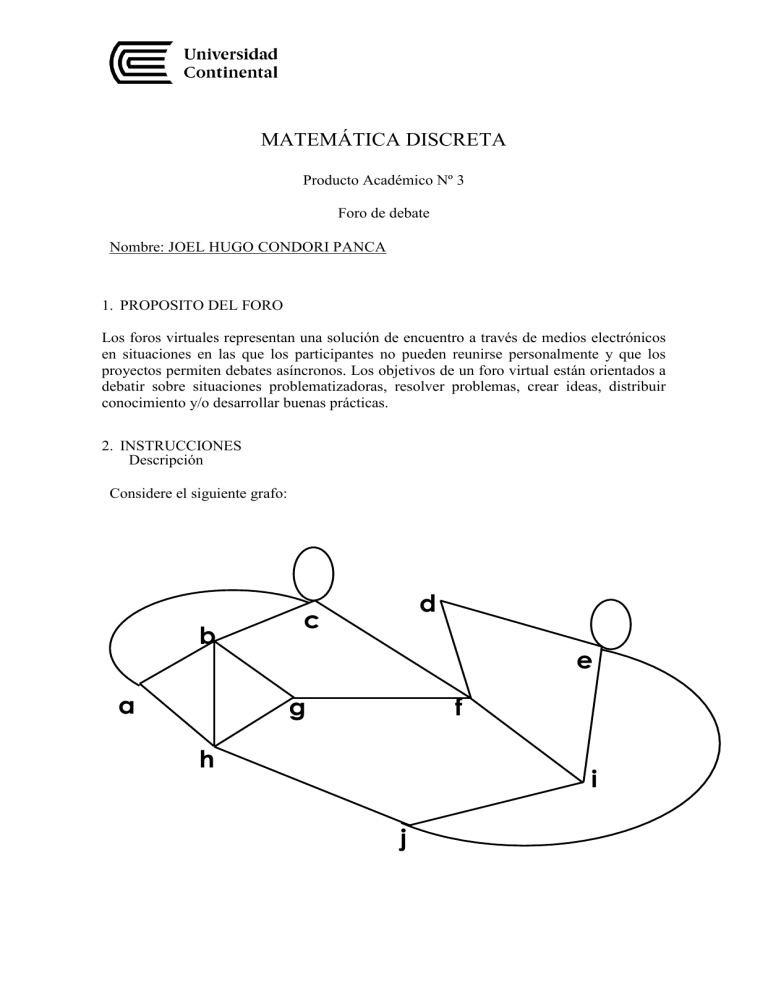
Considere el siguiente grafo:
b
a
d
c
e
g
f
h
i
j
Contestar las siguientes Preguntas y argumentarlas
a) ¿Es un grafo simple?
No es un grafo simple
Un grafo que no tiene bucles ni aristas paralelas se denomina grafo
simple., existe bucle en c
b) ¿Es un grafo completo?
Es grafo completo
Un grafo simple que tiene n vértices y cada vértice es adyacente a todos los
demás se denomina GRAFO COMPLETO
c) ¿Es un grafo bipartito completo?
No es grafico bipartito
Porque un grafo bipartito completo está formado por dos conjuntos disjuntos de
vértices y todas las posibles aristas que unen esos vértices
d) ¿Es un grafo conexo?
Si es conexo
Se dice que un grafo es conexo, si existe un camino simple entre cualesquiera
dos vértices diferentes
e) ¿Tiene un camino euleriano?
No Tiene un camino euleriano
Porque los vértices como ejemplo a,g,j no son de grado par
f) ¿Tiene un circuito euleriano?
Si como ejemplo: abchgf
g) Obtener:
➢ El conjunto de vértices
V={a,b,c,d,e,f,g,h,j,i}
➢ El conjunto de aristas
E={(a,b), (b,a), (b,c), (c,b), (a,c), (c,a), (a,h), (h,a), (h,b), (b,h), (g,b),
(b,g), (g,f), (f,g), (g,h), (h,g), (g,f), (f,g), (c,f), (f,c), (h,j), (j,h), (j,i), (i,j),
(j,e), (e,j), (f,i), (i,f), (i,e), (e,i), (e,d), (d,e), (f,d), (d,f)}
➢ El conjunto de bucles
Bucle={c,e}
➢ El conjunto de aristas paralelas
∅
h) Obtener la matriz de adyacencia y la matriz de incidencia
a
b
c
d
e
f
g
h
i
j
grado
a
0
1
0
0
0
0
0
1
0
0
2
b
1
0
1
0
0
0
1
1
0
0
4
c
0
1
1
0
0
1
0
0
0
0
3
d
0
0
0
0
1
1
0
0
0
0
2
e
0
0
0
1
1
0
0
0
1
0
3
f
0
0
1
1
0
0
1
0
1
0
4
g
0
1
0
0
0
1
0
1
0
0
3
h
1
1
0
0
0
0
1
0
0
0
3
i
0
0
0
0
1
1
1
0
0
0
3
j
0
0
0
0
1
0
0
1
1
0
3
E17
E1
b
c
E3
d
E7
e12
e11
E2
E18
e
E6
E9
E5
aE
8
E8
g
f
E4
h
e13
E10
E15
e14
i
E16
j
a
1
1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
e1
e2
e3
e4
e5
e6
e7
e8
e9
e10
e11
e12
e13
e14
e15
e16
e17
e18
b
0
1
1
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
c
0
0
1
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
d
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
e
0
0
0
0
0
0
0
0
0
0
0
1
0
0
1
0
0
1
f
0
0
0
0
0
0
0
0
1
0
1
0
0
1
0
0
0
0
g
0
0
0
0
0
1
0
1
1
0
0
0
0
0
0
0
0
0
h
0
0
0
1
1
0
0
1
0
0
0
0
0
0
0
0
0
0
i
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
0
0
0
j
0
0
0
0
0
0
0
0
0
1
0
0
1
0
0
1
0
0
h) ¿Cuál es la valencia de cada uno de los vértices?
grado
a
2
b
4
c
3
d
2
e
3
f
4
g
3
h
3
i
3
j
3











