UNIVERSIDAD MARIANO GALVEZ COATEPEQUE, QUETZALTENANGO GUATEMALA, C.A. TRABAJO DE INVESTIGACION
Anuncio

UNIVERSIDAD MARIANO GALVEZ
COATEPEQUE, QUETZALTENANGO
GUATEMALA, C.A.
TRABAJO DE INVESTIGACION
MATEMATICA DISCRETA
MATEMATICA DISCRETA
UNION: "
A"B={X|X"AVX"B}
Ejemplo:
A = { 0, 1, 2, 3, 4, 5 } B = { 1, 3, 5, 7, 9 } = A " B = { 0, 1, 2, 3, 4, 5, 7, 9 }
AB
A"B=
INTERSECCION: "
A"B={X|X"A"X"B}
Ejemplo:
A = { 0 , 1, 2, 3, 4, 5 } B = { 1, 3, 5, 7, 9 } = A " B = { 1, 3, 5 }
AB
A"B=
DIFERENCIA: %
A%B={X|X"A"X"B}
Ejemplo:
A = { 0, 1, 2, 3, 4, 5 } B = { 1, 3, 5, 7, 9 } = A % B = { 0, 2, 4 }
AB
A%B=
AB
1
B%A=
DIFERENCIA SIMETRICA: %
A % B = {X | X " ( A − B ) V X " ( B − A ) }
Ejemplo:
A = { 0, 1, 2, 3, 4, 5 } B = { 1, 3, 5, 7, 9 } = A % B = { 0, 2, 4, 7, 9 }
AB
A%B=
RELACION DE PERTENENCIA:
Es Verificar si algún elemento de un conjunto pertenece a otro conjunto. Se representa por : "
Ejemplo:
De acuerdo al siguiente conjunto, verificar la relación de pertenencias:
E
AB9"A5"A
30 " B 30 " E
3 "A3 "B
10 " E 10 " A
RELACION DE CONTENCION:
Es verificar si un elemento de un conjunto está contenido en otro conjunto. Su símbolo es: "
Ejemplo:
A = { 0, 1, 2 } B = { 0, 1, 2, 3, 4, 5 } C = { 2, 0, 1 }
D = { 1, 3, 5 } E = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, }
A"BA"CA"DB"DC"DC"E
E"BC"BB"C
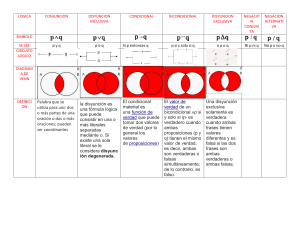
DEFINICIONES
LOGICA
Es la disciplina que trata del método del razonamiento.
2
PROPOSICION:
Es una oración que declara que algo es Verdadero o Falso ( V / F ), pero no ambos.
RAZONAMIENTO INDUCTIVO:
Es aquel que a partir de un número de observaciones particulares se concluyen leyes generales o sea casos
particulares a idea generales.
METODO DEDUCTIVO:
Concluimos ciertos pensamientos particulares a partir de otros generales. Ej. Todas las ballenas son
mamíferas; todos los mamíferos tienen pulmones; conclusión: Las ballenas tienen pulmones.
METODO INTUITIVO:
De ahí corazonadas, presentimientos, intuición. Etc.
Las proposiciones por lo general se escriben con letras minúsculas: p, q, r, s . Ej. p: la tierra es redonda.
OPERADORES DE LA PORPOSICION COMPUESTA:
NEGACION: ~
p q p −p
Método Binario:
VFV=110
FVF=001
COMPUERTA: NOT
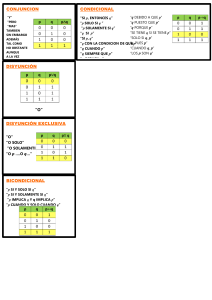
CONJUNCION:
p q p q Método Binario: p q p . q Cuando las dos sean
Verdaderas, la con−
V V V 1 1 0 junción será verdade−
F V F 1 0 0 ra, las demás, falsas.
FVF010
FFF000
COMPUERTA: AND p
q
3
DISYUNCION:
Dentro de la Disyunción existe la Disyunción Inclusiva y la Disyunción Exclusiva.
DISYUNCIÓN INCLUSIVA:
p q p V q Método Binario: p q p V q Con una que sea verdadera
La disyunción será ver−
V V V 1 1 1 dadera.
VFV101
FVV011
FFV000
COMPUERTA : OR
DISYUNCION EXCLUSIVA:
Cuando las dos sean iguales,
La disyunción Exclusiva será falsa,
y si son diferentes, Será verdadera.
Método Binario:
pqpVqpqpVq
VVF110
VFV101
FVV011
FFF000
COMPUERTA EXCLUSIVA :
PROPOSICION CONDICIONAL:
p q p q Método Binario p q p q Cuando el Antecedente es Verdadero
4