Resumen de Test de Hipótesis
Anuncio

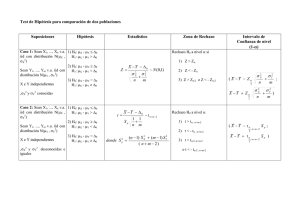
Resumen de Test de Hipótesis
Test de Medias Exactos
2
Caso 1: Sean X1 ; X2 ; :::; Xn iid N ( ;
Hipotesis N ula
H0 :
=
Z=
0
Donde PH0 (Z
X
S2
=
X
=
X2
=
n
2
2
) con
desconocida
Estad{stico Bajo H0
T =
0
Hipotesis Alternativa
H1 : < 0
H1 : > 0
H1 : 6= 0
:
N (0; 1)
0
p
z )=1
n
1P
=
Xi
n i=1
Hipotesis N ula
Donde
X
Criterios de Rechazo
zobservado
z
zobservado z
jzobservado j z a2
Caso 2: Sean X1 ; X2 ; :::; Xn iid N ( ;
=
conocida.
Estad{stico Bajo H0
Hipotesis Alternativa
H1 : < 0
H1 : > 0
H1 : 6= 0
H0 :
2
) con
X
S
p
n
t(n
0
Criterios de
tobservado
tobservado
jtobservado j
PH0 (T t(n
n
1 P
Xi
n 1 i=1
n
1P
Xi
n i=1
n
1P
X2
n i=1 i
1)
1)
Rechazo
t(n 1)
t(n 1)
t(n 1) a2
)=1
X
2
=
n
n
1
h
X2
X
2
i
Caso 3: Sean X1 ; X2 ; :::; Xn iid N ( X ; 2X ) y sean Y1 ; Y2 ; :::; Ym iid
N ( Y ; 2Y ) con 2X y 2Y conocidas. Con Xi independiente de Yj para
todo i y para todo j
1
Hipotesis N ula
H0 : X
Y =
Estad{stico Bajo H0
X Y
o
Z=r
N (0; 1)
2
2
0
X
n
Hipotesis Alternativa
H1 : X
0
Y
H1 : X
0
Y
H1 : X
0
Y 6=
Donde PH0 (Z
X
Y
+
Y
m
Criterios de Rechazo
zobservado
z
zobservado z
jzobservado j z a2
z )=1
n
1P
=
Xi
n i=1
m
1 P
Yi
=
m i=1
Caso 4: Sean X1 ; X2 ; :::; Xn iid N ( X ; 2X ) y sean Y1 ; Y2 ; :::; Ym iid
N ( Y ; 2Y ) con 2X y 2Y desconocidas e iguales. Con Xi independiente de Yj para todo i y para todo j
Hipotesis N ula
H0 : X
Y =
0
Hipotesis Alternativa
H1 : X
0
Y
H1 : X
0
Y
H1 : X
0
Y 6=
Estad{stico Bajo H0
T = X pY 1 1o
tn+m
SP
n+m
Criterios de Rechazo
tobservado
t(n+m 2)
tobservado t(n+m 2)
jtobservado j t(n+m 2) a2
2
2
Donde
:
X
=
Y
=
SP2
=
2
SX
=
SY2
=
X2
=
Y2
=
PH0 (T
n
1P
Xi
n i=1
m
1 P
Yi
m i=1
t(n+m
2)
)=1
2
1)SX
+ (m 1)SY2
n+m 2
n
1 P
n h 2
2
Xi X =
X
n 1 i=1
n 1
m
n h 2
1 P
2
Y
Yi Y =
m 1 i=1
n 1
n
1P
X2
n i=1 i
m
1 P
Y2
m i=1 i
(n
X
Y
2
2
i
i
Caso 5: Sean X1 ; X2 ; :::; Xn iid N ( X ; 2X ) y sean Y1 ; Y2 ; :::; Yn iid
N ( Y ; 2Y ). Con Xi no necesariamente independientes de Yj para todo
i y para todo j: Entonces
Xi
Yi = Di i = 1; 2; 3:::; n
Di
N ( D ; 2D ) i = 1; 2; 3:::; n
E(Di ) =
D
2
V (Di ) =
D conocida
H0 :
Hipotesis N ula
X
Y = D =
0
Estad{stico Bajo H0
r o
Z=D
N (0; 1)
2
D
n
Hipotesis Alternativa
H1 : X
0
Y = D
H1 : X
=
0
Y
D
H1 : X
=
0
Y
D
Donde PH0 (Z
D
Criterios de Rechazo
zobservado
z
zobservado z
jzobservado j z a2
z )=1
n
1P
=
Xi
n i=1
3
Caso 6: Sean X1 ; X2 ; :::; Xn iid N ( X ; 2X ) y sean Y1 ; Y2 ; :::; Yn iid
N ( Y ; 2Y ). Con Xi no necesariamente independientes de Yj para todo
i y para todo j: Entonces
Xi
Yi = Di i = 1; 2; 3:::; n
Di
N ( D ; 2D ) i = 1; 2; 3:::; n
E(Di ) =
D
2
V (Di ) =
D desconocida
Hipotesis N ula
H0 : X
Y =
Estad{stico Bajo H0
T = X Yp 1 o
tn 1
0
S
Hipotesis Alternativa
H1 : X
0
Y
H1 : X
0
Y
H1 : X
0
Y 6=
Donde
:
D
=
2
SD
=
D2
=
n
Criterios de
tobservado
tobservado
jtobservado j
PH0 (T t(n
n
1P
Di
n i=1
n
1 P
Di
n 1 i=1
n
1P
D2
n i=1 i
1)
Rechazo
t(n 1)
t(n 1)
t(n 1) a2
)=1
D
2
=
n
n
1
h
D2
D
2
i
Test de Medias Asintóticos
Caso 7: Sean X1 ; X2 ; :::; Xn iid Be(p) con p desconocida y n grande.
Hipotesis N ula
H 0 : p = p0
Estad{stico Bajo H0
p0
Z = qpbp(1
N (0; 1)
b
p)
b
n
Hipotesis Alternativa
H1 : p < p 0
H1 : p > p 0
H1 : p 6= p0
Criterios de Rechazo
zobservado
z
zobservado z
jzobservado j z a2
Donde PH0 (Z
z )=1
n
1P
Xi
pb =
n i=1
4
Caso 8: Sean X1 ; X2 ; :::; Xn iid F (x) tal que E(Xi ) =
discretas o continuas) y n grande.
Hipotesis N ula
H0 :
=
Estad{stico Bajo H0
Z=
0
Hipotesis Alternativa
H1 : < 0
H1 : > 0
H1 : 6= 0
Donde
:
S2
=
X
=
X2
=
(Pueden ser
X
S
p
n
N (0; 1)
0
Criterios de Rechazo
zobservado
za
zobservado za
jzobservado j t(n 1) a2
PH0 (Z za ) = 1
n
1 P
Xi X
n 1 i=1
n
1P
Xi
n i=1
n
1P
X2
n i=1 i
2
=
n
n
1
h
X2
X
2
i
Caso 9: Sean X1 ; X2 ; :::; Xn iid Be(pX ) y sean Y1 ; Y2 ; :::; Ym iid Be(pY )
con pX y pY desconocidas. Con Xi independiente de Yj para todo i y
para todo j: Con m y n grandes
Hipotesis N ula
H 0 : p X pY = 0
Estad{stico Bajo H0
Z=
q
Hipotesis Alternativa
H1 : X
0
Y
H1 : X
0
Y
H1 : X
0
Y 6=
p
bX p
bY
o
p
bY (1 p
bY )
p
bX (1 p
bX )
+
n
m
N (0; 1)
Criterios de Rechazo
zobservado
z
zobservado z
jzobservado j z a2
Donde PH0 (Z
pbX
pbY
z )=1
n
1P
=
Xi
n i=1
m
1 P
=
Yi
m i=1
5
Caso 10: Sean X1 ; X2 ; :::; Xn iid FX (x) y sean Y1 ; Y2 ; :::; Ym iid FY (y)
tal que E(Xi ) = X y E(Yi ) = Y (Pueden ser discretas o continuas)
con n y m grande. Con Xi independiente de Yj para todo i y para
todo j
Hipotesis N ula
H0 : X
Y =
0
Estad{stico Bajo H0
X Y
o
N (0; 1)
Z=r
2
2
S
X
n
Hipotesis Alternativa
H1 : X
0
Y
H1 : X
0
Y
H1 : X
0
Y 6=
Donde
:
X
=
Y
=
2
SX
=
SY2
=
X2
=
Y2
=
+
S
Y
m
Criterios de Rechazo
zobservado
za
zobservado z
jzobservado j z 2
PH0 (z za ) = 1
n
1P
Xi
n i=1
m
1 P
Yi
m i=1
n
1 P
Xi X
n 1 i=1
m
1 P
Yi Y
m 1 i=1
n
1P
X2
n i=1 i
m
1 P
Y2
m i=1 i
2
2
=
=
n
n
1
n
n
1
h
h
X2
X
Y2
Y
2
2
i
i
Test de Varianzas
Caso 11: Sean X1 ; X2 ; :::; Xn iid N ( ;
Hipotesis N ula
H0 : 2 = 20
2
) con
conocida.
Estad{stico Bajo H0
2
2
C = nb2
n
0
Hipotesis Alternativa
Criterios de Rechazo
2
2
H1 : 2
Cobservado
0
(n)1
2
2
2
Cobservado
H1 :
0
(n)
2
2
2
H1 :
6= 0
Cobservado
(n) a o Cobservado
2
6
2
(n)1
a
2
2
(n)
n
1P
Donde PH0 (C
b
=
2
2
(Xi
)
) con
desconocida.
n i=1
Caso 12: Sean X1 ; X2 ; :::; Xn iid N ( ;
Hipotesis N ula
H0 : 2 = 20
)=1
Estad{stico Bajo H0
2
2
C = (n 1)S
2
(n 1)
0
Hipotesis Alternativa
Criterios de Rechazo
2
2
H1 : 2
Cobservado
0
(n 1)1
2
2
2
H1 :
Cobservado
0
(n 1)
2
H1 : 2 6= 20
Cobservado
(n 1) a o Cobservado
2
(n 1)1
2
2
(n 1)
Donde PH0 (C
S2
=
X
=
a
2
)=1
n
P
1
Xi
n 1 i=1
n
1P
Xi
n i=1
X
2
Caso 13: Sean X1 ; X2 ; :::; Xn iid N ( X ; 2X ) y sean Y1 ; Y2 ; :::; Ym iid
N ( Y ; 2Y ) con X y Y desconocidas e iguales. Con Xi independiente
de Yj para todo i y para todo j
Hipotesis N ula
H0 : 2X = 2Y
Estad{stico Bajo H0
S2
F = SX2
F(n 1);(m 1)
Y
Hipotesis Alternativa
2
H1 : 2X
Y
2
2
H1 : X
Y
H1 :
2
X
6=
2
Y
Fobservado
Fobservado
F(n
7
1);(m 1)( 2 )
Criterios de Rechazo
F(n 1);(m 1)(1 ) = F(m
Fobservado F(n 1);(m 1)(
o Fobservado
F(n
1
1);(n 1)( )
)
1);(m 1)(1
2)
h
= F(m
1);(n 1)( 2 )
i
1
Donde PH0 (F
2
SX
=
X
=
SY2
=
Y
=
F(n 1);(m 1)( ) ) = 1
n
1 P
2
Xi X
n 1 i=1
n
1P
Xi
n i=1
m
1 P
2
Yi Y
m 1 i=1
m
1 P
Yi
m i=1
Caso 14: Sean X1 ; X2 ; :::; Xn iid N ( X ; 2X ) y sean Y1 ; Y2 ; :::; Ym iid
N ( Y ; 2Y ) con X y Y conocidas e iguales. Con Xi independiente de
Yj para todo i y para todo j
Hipotesis N ula
H0 : 2X = 2Y
Estad{stico Bajo H0
b2
F = bX
F(n);(m)
2
Y
Hipotesis Alternativa
2
H1 : 2X
Y
2
2
H1 : X
Y
H1 :
2
X
6=
2
Y
Criterios de Rechazo
Fobservado F(n);(m)(1 ) = F(m);(n)(
Fobservado F(n);(m)( )
Fobservado
Donde PH0 (F
b2X
b2Y
X
F(n);(m)( 2 ) o Fobservado
F(n 1);(m
n
1P
(Xi
=
n i=1
m
1 P
=
(Yi
m i=1
=
Y
8
1)( ) )
2
X)
2
Y
)
=1
F(n);(m)(1
2)
1
)
h
i
= F(m);(n)( 2 )
1