Tests Exactos - ditellianos.org
Anuncio
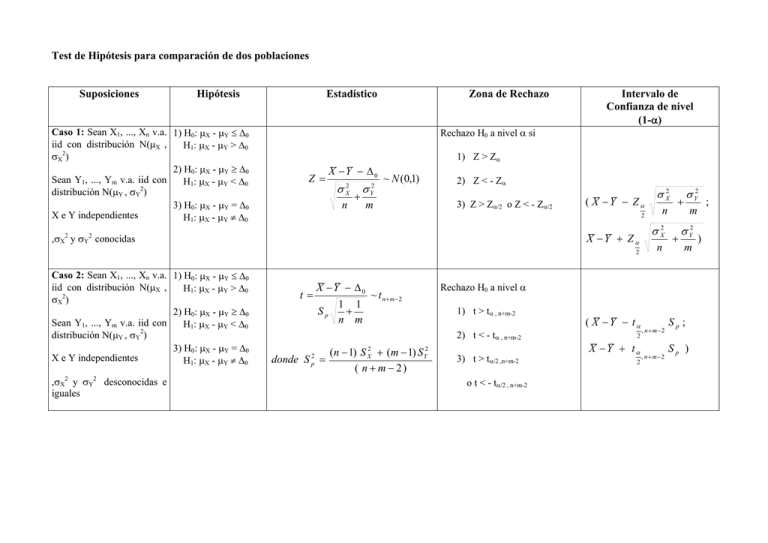
Test de Hipótesis para comparación de dos poblaciones Suposiciones Hipótesis Caso 1: Sean X1, ..., Xn v.a. 1) H0: μX - μY ≤ Δ0 iid con distribución N(μX , H1: μX - μY > Δ0 σX2) 2) H0: μX - μY ≥ Δ0 Sean Y1, ..., Ym v.a. iid con H1: μX - μY < Δ0 distribución N(μY , σY2) 3) H0: μX - μY = Δ0 X e Y independientes H1: μX - μY ≠ Δ0 Estadístico Zona de Rechazo Intervalo de Confianza de nivel (1-α) Rechazo H0 a nivel α si 1) Z > Zα Z = X −Y − Δ0 σ X2 n + σ Y2 ~ N (0,1) m 2) Z < - Zα 3) Z > Zα/2 o Z < - Zα/2 ( X −Y − Zα 2 X −Y + Zα ,σX2 y σY2 conocidas 2 Caso 2: Sean X1, ..., Xn v.a. 1) H0: μX - μY ≤ Δ0 iid con distribución N(μX , H1: μX - μY > Δ0 2 σX ) 2) H0: μX - μY ≥ Δ0 Sean Y1, ..., Ym v.a. iid con H1: μX - μY < Δ0 distribución N(μY , σY2) 3) H0: μX - μY = Δ0 X e Y independientes H1: μX - μY ≠ Δ0 ,σX2 y σY2 desconocidas e iguales t= X −Y − Δ0 Sp 1 1 + n m ~ t n+ m−2 (n − 1) S X2 + (m − 1) S Y2 ( n + m − 2) n σ X2 n σ Y2 + + m σ Y2 m Rechazo H0 a nivel α 1) t > tα , n+m-2 2) t < - tα , n+m-2 donde S p2 = σ X2 3) t > tα/2 ,n+m-2 o t < - tα/2 , n+m-2 ( X −Y − tα 2 X −Y + tα 2 , n+m−2 , n+m−2 Sp ; Sp ) ) ; Caso 3: Sean X1, ..., Xn v.a. 1) H0: μX - μY ≤ Δ0 iid con distribución N(μX , H1: μX - μY > Δ0 σX2) 2) H0: μX - μY ≥ Δ0 Sean Y1, ..., Yn v.a. iid con H1: μX - μY < Δ0 distribución N(μY , σY2) 3) H0: μX - μY = Δ0 X e Y no independientes H1: μX - μY ≠ Δ0 ,σX2 y σY2 desconocidas t= D − Δ0 ~ t n −1 SD n Rechazo H0 a nivel α si 1) t > tα , n-1 2) t < - tα , n-1 ( X −Y − tα 2 donde 3) t > tα/2 ,n-1 o t < - tα/2 , n-1 Di = X i − Yi 2 D = X −Y n S D2 = ∑( D i =1 i X −Y + tα − D )2 n −1 , n −12 , n −1 SD ; SD ) Tests Asintóticos Suposiciones Hipótesis Caso 4: Sean X1, 1) H0: μX - μY ≤ Δ0 ..., Xn v.a. iid con H1: μX - μY > Δ0 E(Xi) = μX Var (Xi) = σX2 2) H0: μX - μY ≥ Δ0 H1: μX - μY < Δ0 Sean Y1, ..., Ym v.a. iid con 3) H0: μX - μY = Δ0 E(Xi) = μY Var H1: μX - μY ≠ Δ0 (Xi) = σY2 Estadístico Zona de Rechazo Intervalo de Confianza de nivel (1-α) Rechazo H0 a nivel α si Z = X −Y − Δ0 σ X2 n + σ Y2 ≈ N (0,1) 3) Z > Zα ( X −Y − Zα 2 4) Z < - Zα m X −Y + Zα 4) Z > Zα/2 2 σ X2 n σ X2 n + + σ Y2 ; m σ Y2 m ) o Z < - Zα/2 X e Y independientes n y m grandes Caso 5: Sea X ~ 1) H0: p1 – p2 ≤ 0 Bi (n , p1) H1: p1 – p2 > 0 Sea Y ~ Bi (m , 2) H0: p1 – p2 ≥ 0 p2) H1: p1 – p2 < 0 X e Y 3) H0: p1 – p2 = 0 independientes H1: p1 – p2 ≠ 0 n y m grandes pˆ 1 − pˆ 2 pˆ 1 (1 − pˆ 1 ) pˆ 2 (1 − pˆ 2 ) + n m X Y donde pˆ 1 = pˆ 2 = n m Z= Rechazo H0 a nivel α si 1) Z > Zα ( pˆ 1 − pˆ 2 − Z α 2 2) Z < - Zα 3) Z > Zα/2 o Z < - Zα/2 pˆ 1 − pˆ 2 + Z α 2 pˆ 1 ( 1 − pˆ 1 ) pˆ 2 ( 1 − pˆ 2 ) + ; n m pˆ 1 ( 1 − pˆ 1 ) pˆ 2 ( 1 − pˆ 2 ) + ) n m