Una escalera de bomberos de 10 m

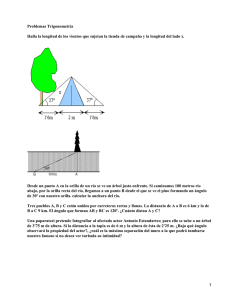
Una escalera de bomberos de 10 m. de longitud se ha fijado en un punto de la calzada. Si se
apoya sobre una fachada forma un ángulo con el suelo de 45º y si se apoya sobre la
fachada opuesta forma un ángulo de 30º.
a) Hallar la anchura de la calle.
b) ¿Qué altura se alcanza con dicha escalera en cada una de las fachadas?
c) Dos escaleras de 10 m. están colocadas en el centro de la calle y se encuentran
apoyadas sobre las fachadas de los ejercicios anteriores. Calcular el ángulo formado
por las dos escaleras entre sí.
Resolución:
a) La anchura de la calle es x + y . Para
calcular x , aplicamos que cos 45 =
x
;
10
2
x
=
⇔ 2 x = 10 2 ⇔ x = 5 2 m.
2
10
Para calcular la y , aplicamos lo mismo a
y
3 y
⇔
=
⇔ 2 y = 10 3 ⇔ y = 5 3
10
2 10
m. Así pues la anchura de la calle será: x + y = 5 2 + 5 3 = 5( 2 + 3 ) m.
cos 30 =
b) Altura que se alcanza en la fachada izquierda: Como el ángulo que forma la escalera
es de 45º, se trata de un triángulo isósceles, por tanto la altura será la misma que la
anchura, es decir h = 5 2 m.
Altura que se alcanza en la fachada derecha: Podemos aplicar el teorema de Pitágoras o
bien la fórmula del seno de 30º. Optaremos por esta última y así:
sen30 =
h
1 h
⇔ =
⇔ h = 5 m.
10
2 10
L.Roche Ramón, 2006
Pág. 1 de 2
c) La calle mide 5( 2 + 3 ) m., con lo que
si la escalera está situada en mitad de la
misma, cada uno de los lados medirá
5( 2 + 3 )
m.
2
Tenemos que averiguar el ángulo α y para
ello necesitamos conocer los ángulos A y B
(Observa que son iguales). Conocemos el cateto contiguo y la hipotenusa, con lo que
aplicaremos la definición de coseno. Así:
5( 2 + 3 )
2
cos A =
=
10
2+ 3
= 0,7865 , con lo que A = 38º 8’ 3.28’’
4
Como A=B, α = 180 − 2 A
α=103º 43’ 53.4’’
Inicio del problema
L.Roche Ramón, 2006
Pág. 2 de 2