Estudio experimental de la Fuerza Centrípeta - Física re

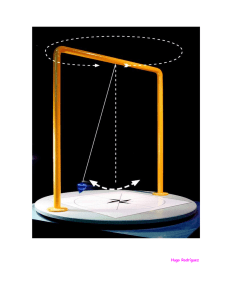
Estudio experimental de la Fuerza
Centrípeta
Carrió, Diego
Leibovich, Débora
Molas, Cecilia
Rodriguez Riou, Florencia
carriod@uol.com.ar
debbie@megabras.com
cecimolas@hotmail.com
florrr14@hotmail.com
Fundación universitaria R. Favaloro
Se desea estudiar la dependencia de la fuerza centrípeta en un movimiento circular
respecto del radio de la circunferencia, de la masa de la partícula y de la velocidad de
dicha masa. Para esto se analiza como sistema un péndulo simple, ya que éste es
describe un movimiento circular no uniforme.
Introducción:
Un péndulo simple es un modelo idealizado que consiste en una masa puntual
suspendida de un hilo sin masa no extensible. Al desplazar la masa de su punto de
equilibrio, ésta oscila alrededor de dicha posición. La masa puntual describe un arco de
circunferencia con radio l igual a la longitud del hilo.
Por ser un movimiento circular, la componente radial de la fuerza neta debe ser:
→
∑F r =
mv 2
= T- m.g.cosθ
l
(1)
Entonces,
T = m.(g.cosθ +
v2
)
l
(2)
Para θ = 0º:
T = m.( g +
Fuerza centripetal - Carrió et al,
v2
)
l
(3)
1
Arreglo Experimental:
DeDDe
Figura 1. Esquema de un péndulo simple con una obstrucción cilíndrica de diámetro
d para determinar la velocidad del péndulo y la tensión de la cuerda en su posición de
equilibrio.
Para realizar este trabajo, se cuelga un péndulo de un sensor de fuerza conectado a
la PC para medir la tensión Fy en el hilo. De esta señal senoidal se toma el valor pico ya que
éste corresponde al valor de la tensión para θ = 0º.
Además se coloca un fotointerruptor, de forma tal de medir el intervalo de tiempo
durante el cual el cilindro de material opaco colocado en la parte inferior del péndulo
interrumpe el haz de luz al pasar por la posición de equilibrio. Conociendo el diámetro del
cilindro, que se mide en forma directa con un calibre, se calcula la velocidad media del
péndulo.
La longitud del hilo se mide en forma directa con un cinta métrica.
La velocidad y la tensión en el punto de equilibrio se miden para los siguientes casos:
•
•
Para distintas longitudes, manteniendo constante la masa.
Para distintas masas, manteniendo constante la longitud.
Fuerza centripetal - Carrió et al,
2
4.0
3.5
3.0
2.5
2.0
1.5
1.0
0.5
T [N]
T [N]
Resultados:
y = 0.3565x + 1.8457
R2 = 0.9941
0
1
2
3
4
3.5
3
2.5
2
1.5
1
0.5
0
5
y = 0.2985x + 1.866
R2 = 0.9891
0
1
V^2 [m^2/s^2]
2
3.5
3
2.5
2
1.5
1
0.5
0
y = 0.2565x + 1.8442
R2 = 0.9935
1
4
5
(b)
T [N]
T [N]
(a)
0
3
V^2 [m^2/s^2]
2
3
4
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
y = 0.2104x + 1.8454
R2 = 0.9985
0
5
1
2
3
4
5
6
V^2 [m^2/s^2]
V^2 [m^2/s^2]
(c)
(d)
Figura 2: Representación gráfica de la tensión en el hilo en función del cuadrado de la velocidad
en la posición de equilibrio para una masa de 0,188 kg y longitud de (a) 0,52 m (b) 0,60 m (c) 0,73
m (d) 0,85 m.
3.5
3
2.5
2
1.5
1
0.5
0
6
5
T [N]
T [N]
En la figura 2 se observa que la dependencia de la tensión en función de longitud. La
pendiente de T versus v2 para masa constante de valor m = 0,188 kg disminuye a medida
que aumenta la longitud, y en cada caso es aproximadamente igual a m/l. La ordenada al
origen resulta independiente de la longitud, y aproximadamente igual a m.g.
y = 0.2985x + 1.866
R2 = 0.9891
4
3
2
y = 0.5123x + 3.0235
R2 = 0.9886
1
0
0
1
2
3
V^2 [m^2/s^2]
(a)
Fuerza centripetal - Carrió et al,
4
5
0
1
2
3
4
5
V^2 [m^2/s^2]
(b)
3
8
7
T [N]
6
5
4
3
2
y = 0.5938x + 3.6619
R 2 = 0.9979
1
0
0
1
2
3
4
5
6
V^2 [m^2/s^2]
(c)
Figura 3: Representación gráfica de la tensión en el hilo en función del cuadrado de la velocidad
en la posición de equilibrio para una longitud de 0,60 m y masa de a) 0,188 Kg b) 0,307 Kg c)
0,371 Kg.
En la figura 3 se observa la dependencia de la tensión en función de masa. La pendiente de
T vs. v 2 para longitud constante de valor l = 0,6m aumenta a medida que aumenta la masa,
y en cada caso es aproximadamente igual a m/l. La ordenada al origen también varía, y
resulta aproximadamente igual a m.g.
0.3
k [Kg/m]
k [Kg/m]
0.4
0.2
y = 0.1883x - 0.0084
R2 = 0.9904
0.1
0
0
0.5
1
1.5
2
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
2.5
y = 1.6368x - 0.0043
R2 = 0.9934
0
0.1
1/l [1/m]
0.2
0.3
0.4
m [Kg]
c [N]
Figura 4: Representación gráfica de la pendiente
de los gráficos de T vs. v 2 para m=0,188kg , en
función de la inversa de la longitud.
4
3.5
3
2.5
2
1.5
1
0.5
0
Figura 5: Representación gráfica de la
pendiente de los gráficos de T vs. v 2 para
l=0,6m , en función de la masa.
y = 9.8027x + 0.0208
R2 = 1
0
0.1
0.2
m [Kg]
0.3
0.4
Figura 6: Representación gráfica de la ordenada al origen de los gráficos de T vs. v 2 para l=0,6m
en función de la masa.
Las figuras 4, 5 y 6 permiten visualizar más claramente la forma de la relación lineal de T
vs. v2 . Se observa que la pendiente es directamente proporcional a la masa e inversamente
proporcional a la longitud del hilo, y que la ordenada al origen es proporcional a la masa
con una constante de proporcionalidad aproximadamente igual a g.
Fuerza centripetal - Carrió et al,
4
4.0
3.5
T [N]
3.0
2.5
2.0
1.5
y = 0.9999x + 1.8444
R2 = 0.9962
1.0
0.5
0.0
0.0
0.5
1.0
m*v^2/l [N]
1.5
2.0
Figura 7: Representación gráfica de la tensión en el hilo en la posición de equilibrio en función del
término m*v^2/l para m=0,188 kg
Por último, en la figura 7 se observa claramente que la relación T versus m.v2/l es lineal, de
pendiente 1 y ordenada al origen igual a m.g.
Conclusión:
Se verifica experimentalmente que la tensión en el hilo de un péndulo simple en la posición
de equilibrio está dada por:
v2
)
T = m.( g +
(4)
l
Esto es equivalente a afirmar que la fuerza centrípeta viene dada por la relación mv2/l.
Bibliografía:1.
2.
Física Universitaria, Volumen I, Sears-Zemansky, Addison Wesley, EE.UU., 1996.
Física re-Creativa, S.Gil y E. Rodríguez http://www.fisicarecreativa.com
Fuerza centripetal - Carrió et al,
5