Se colocan en posición vertical dos placas metálicas
Anuncio

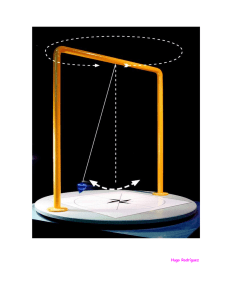
Se colocan en posición vertical dos placas metálicas paralelas, separadas 10 cm y se las carga a 2.104 V. Entre las placas se dispone un péndulo eléctrico constituido por una esferita metálica de 2 mm de diámetro y 7,8 g/cm3 de densidad que se ha cargado a 2000 V, suspendida de un hilo de masa despreciable. Determina la posición de equilibrio del péndulo. Solución E Observa que el potencial de la esfera es positivo (2000 V), lo que significa que está carga da positivamente. Entonces, como Fe qE , la fuerza eléctrica que el condensador ejerce sobre ella tiene el mismo sentido que E ; es decir es horizontal y dirigida hacia la izquierda, como se ve en la figura. Dicho de otra forma, la esfera es atraída por la placa negativa del condensador y repelida por la positiva, lo que hace que el hilo del péndulo se desplace hacia la izquierda. Tv T Fe Th De acuerdo con el esquema de fuerzas de la figura, el péndulo alcanzará la posición de equilibrio cuando la resultante de las fuerzas que actúan sobre él sea cero, es decir, P T P Fe Th Fe 0 Tv P T sin Fe T cos mg donde Th y Tv son, respectivamente, las magnitudes de las componentes horizontal y vertical de la tensión del hilo. Dividiendo miembro a miembro las dos últimas ecuaciones, Fe mg tan qE mg donde q es la carga de la esfera del péndulo, que tenemos que hallar para obtener . La esfera conductora se comporta como una partícula de la misma carga situada en su centro. Así pues, el potencial en un punto de su superficie, situado a una distancia R del centro, es, V k0 q R V R k0 q 2000 2 10 3 9 9 10 4 10 9 C 9 La masa de la esfera la podemos hallar a partir de su densidad, d m V m (4 3) R 3 4 d R3 3 m 4 g 7,8 3 3 cm (0,2 cm)3 0,261 g 2,61 10 4 kg El campo eléctrico se obtiene con la ecuación, E V V d 2 104 V 0,1 m 2 105 V N m C Ahora ya podemos hallar el ángulo, tan qE mg (4 9) 10 2,61 10 9 4 2 105 9,81 0,0347 α =1,99º