Primer Repaso Matemáticas II 1. Si t segundos es el tiempo para
Anuncio

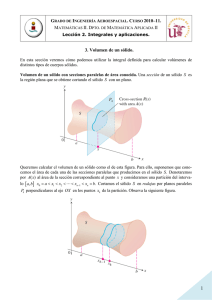
ITESM-CEM Programa Principia Primer Repaso Matemáticas II 1. Si t segundos es el tiempo para una oscilación completa de un péndulo de x pies de longitud, entonces 4 2 x g t 2 , donde g = 32.2. Utiliza diferenciales para estimar el efecto que tiene sobre el tiempo cometer un error de 0.01 al medir la longitud del péndulo. 1 2. La gráfica que se muestra abajo corresponde a la función f ( x) . 1 ex 1.2 1 0.8 0.6 0.4 0.2 -3 -2 -1 1 2 3 4 -0.2 a) Usa sumas de Riemann con n = 5 para estimar los valores por exceso y defecto del área bajo la curva entre x = 0 y x = 2. b) Calcula el menor valor de n con el cual puedan asegurarse 2 cifras decimales exactas en una aproximación del área del inciso (a) usando sumas de Riemann. c) Supón que existe una función F tal que F ´ ( x) f ( x) y que F ( 1 ) = 2, estima los valores de F ( 1.01) y F ( 1.02). Estima el error cometido al calcular F ( 1.01). x dt d) Sea F ( x) , determina dónde crece y dónde decrece la función F, sus máximos y 0 1 et mínimos (si tiene), su concavidad así como sus puntos de inflexión. Bosqueja la gráfica de F sobre la misma gráfica que se te muestra arriba. Describe lo que ocurre con la gráfica de F a la larga, ¿a qué lo atribuyes? e) Calcula explícitamente a la función F, para ello haz el cambio de variable: u e t y utiliza dz 1 z a la fórmula: Ln C . Con tu cálculo, repite los incisos (a) (ahora, el área 2 2 2a z a z a de manera exacta) y (c). 3. La función G (t ) 3 6t 8 2t 4 2 t ( arctan( x)) 2 dx 2 t indica la posición de un objeto, calcula la rapidez inicial G ´ ( 0 ). 4. La resistencia eléctrica R de un cable es directamente proporcional a su longitud e inversamente proporcional al cuadrado de su diámetro. Si se considera la longitud fija ¿cuál debe ser el error porcentual del diámetro para que el error porcentual de R sea del 3%? 5. La base de un sólido es la región plana del primer cuadrante limitada por la parábola y 14 1 x 2 , el eje de las “ x ” y el eje de las “ y ”. Si las secciones transversales del sólido perpendiculares al eje de las “ x ” son cuadradas, determina el volumen de dicho sólido. Autor: Carlos Daniel Prado Pérez ITESM-CEM Programa Principia 6. Evalúa las siguientes integrales: A) E) x 1 x dx ; arcsenx d x ; C) 1 x2 B) sen( x) cos( x) d x ; F) cos(2 x) 2 0 dx x tan 5 ( x 1)(3 x 1) dx ; G) x 7. Una función f está dada por: f ( x) 3 0 p( x) 8. 2 0 dx ; D) 2 (1 x ) Ln x 5 f ( x)dx , si 0 f ( x)dx 9 e ; 1 x 5 2 2 f ( x)dx 1. 1 sen(t ) dt . Encuentra un polinomio cuadrático 2 t2 2 a bx cx tal que p (0)= f ( 0 ), p ' ( 0 ) = f ' ( 0 ) y p '' ( 0 ) = f ' ' ( 0 ). Una partícula se desplaza a lo largo de una recta. Su posición en el tiempo t es f (t ) donde: u2 1 s2 f (t ) g (u ) du , g (u ) d s . Calcula su aceleración cuando t 2. 4 0 u 1 s 9. Decide con qué método puede hallarse el volumen del sólido obtenido al girar alrededor del eje de las “y” la región limitada por y x 4 x 5 y el eje “x”. Una vez que tengas la decisión haz el cálculo. t2 10. La región encerrada por y Log 7 ( x) , y 49 , x 0 , y 0 se hace girar en torno a la recta x 1 . Calcula el volumen del sólido generado. 11. Encuentra el área limitada por la curva y 2 x 4 (4 x) cuya gráfica se muestra abajo. y 7.5 5 2.5 x -4 -3 -2 -1 -2.5 -5 -7.5 12. Determina el área del plano encerrada por y Autor: Carlos Daniel Prado Pérez arccos x , y x 2 , y 0, y .

![• (1JJ [b [M]](http://s2.studylib.es/store/data/001660247_1-1b1ec3f2af6ce5b36615782edea2e40e-300x300.png)