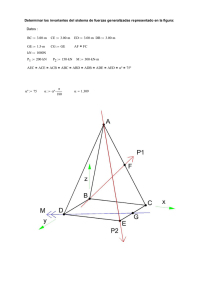
Hallar un vector unitario en la dirección de la resultante
Anuncio

Hallar un vector unitario en la dirección de la resultante de ~a = 2bi b j+b k, ~b = bi + b j + 2b k, ~c = 3bi 2b j + 4b k Solución: El vector resultante es ~ = ~a + ~b + ~c = 2bi b R j+b k + bi + b j + 2b k + 3bi 2b j + 4b k = 6bi 2b j + 7b k Ahora basta dividir entre la magnitud del vector para entonces tener un vector unitario en la misma dirección de la resultante. La magnitud del vector es q p 2 6bi 2b j + 7b k = k(6; 2; 7)k = 62 + ( 2) + 72 = 89 (89 es primo, no se puede reducir más el radical) Así que el vector unitario en la dirección de la resultante es ~ b = R = (6; 2; 7) = (6;p 2; 7) R k(6; 2; 7)k ~ 89 R Resumiendo: b = (6;p 2; 7) R 89 1