tema 5 cinetica del cambio de fase

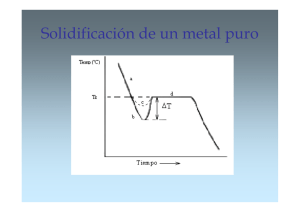
Cinética del cambio de fase
TEMA 5
CINETICA DEL CAMBIO DE FASE
1. INTRODUCCIÓN.
El cambio estructural de un sistema se produce por la existencia de una fuerza conductora de ese cambio. Esta fuerza que impulsa el cambio es la diferencia de energía libre que se
produce en el sistema al producirse el cambio. Sin embargo, el mero hecho de tener esta fuerza
conductora no nos garantiza que la transformación se produzca, es necesario además que exista algún mecanismo que pueda producirlo, éste mecanismo es la difusión. Un proceso de dopado de un semiconductor, se producirá a gran velocidad a alta temperatura, pero será muy
lento a temperaturas bajas, por tanto, la velocidad a la que un proceso de cambio tiene lugar es
función de ambos factores: de la fuerza conductora y de la velocidad, o cinética a la que se
produce, y ambos han de tener valores finitos para que el cambio pueda tener lugar.
Las transformaciones de una fase en otra, como los cambios de fase de un material con
distintos estados alotrópicos, o en general, los cambios estructurales dentro de un sólido, o la
formación de una fase sólida a partir de un líquido, son producidas por mecanismos de difusión. El cambio se produce mediante la formación de pequeñas partículas de la nueva fase que
posteriormente crecen hasta que se produce la transformación completa. Este proceso se denomina de nucleación y crecimiento y como ya se dicho está producido por difusión, proceso
que puede llegar a consumir una gran cantidad de tiempo implicando por tanto pequeñas velocidades de transformación. Existen otros cambios que se producen sin difusión a altas velocidades producidos por pequeños movimientos atómicos alrededor de sus posiciones de equilibrio, estos están gobernados por la propagación de ondas cortantes a través del sólido, este otro
tipo de transformaciones que revisten gran importancia, se tratará en un capitulo posterior.
El crecimiento de un núcleo se produce a través de la interfase producida por la formación del mismo, esta interfase introduce un aumento de energía en el sistema en forma de
energía superficial, ya sea de límite de grano, sólido-líquido etc. La cinética de la transformación estará controlada por parámetros energéticos, siendo la energía libre del sistema la que
marque la situación de equilibrio en cada caso. Otro fenómeno que se produce en toda transformación es la eliminación (si el proceso es de enfriamiento) del calor latente. La mayor o
77
Cinética del cambio de fase
menor dificultad de movimiento
de las partículas en la interfase o
la eliminación del calor latente,
harán que la transformación esté
controlada por uno u otro mecanismo.
2. FUERZA CONDUCTORA
DEL CAMBIO
El proceso de transformación estructural en un mateFigura 1
rial esta condicionado por la
disminución de energía libre que
ocurre en el sistema motivado por el cambio de fase, esta disminución de energía es la fuerza
conductora que origina el proceso de cambio. Vamos a determinar una expresión que nos relacione esta fuerza conductora con la temperatura a la que tiene lugar el fenómeno, y con parámetros conocidos del sólido. Aunque el proceso va ha ser explicado para la solidificación de
un metal, es igualmente válido para una transformación en estado sólido de una fase α a una β,
cambiando la fase líquida por α y la fase sólida por β, y Tm por la temperatura de transformación de ambas fases sólidas.
La energía libre del líquido y sólido, fig. 1, a una temperatura T son:
GL = H L - T S L
(1)
GS = H S - T S S
por tanto a la temperatura T
∆G = ∆H - T∆S
(2)
donde ∆H y ∆S son las diferencias de entalpía y de entropía de líquido a sólido a la temperatura T. A la temperatura de fusión Tm la energía libre del sólido y del líquido son iguales y por
tanto ∆G=0. Por consiguiente:
∆G = ∆H - T m ∆S = 0
78
(3)
Cinética del cambio de fase
despejando ∆S y sustituyendo ∆H por el calor latente de transformación, en éste caso de fusión, Fig. 2, se tiene:
∆S =
∆H
Tm
=
L
(4)
Tm
Esto sólo es válido para la temperatura de transformación y es conocido como entropía
de fusión. Se ha observado que la entropía de fusión es constante para casi todos los metales
(R=8.4 J mol-1 K-1). Esto es lógicamente razonable pues para metales con grandes fuerzas de
enlace es de esperar grandes temperaturas y calores latentes de fusión, con lo
que la relación se mantiene aproximadamente constante. Para pequeños subenfriamientos, ∆T, (diferencias entre la
temperatura de un cambio de fase y la
temperatura a la que tiene lugar la transformación) se puede considerar que tanto ∆H como ∆S son independientes de
la temperatura, combinando por tanto
las dos ecuaciones anteriores se obtiene:
∆G = L - T
L
(5)
Tm
para pequeños ∆T la expresión anterior
se puede poner:
Figura. 2
∆G =
L (T m - T )
L∆T
(6)
Tm
Tm
La expresión anterior nos muestra la variación de energía del sistema al cambiar de fase a una temperatura determinada, cuanto mayor sea ∆T mayor será el cambio energético y mayor la fuerza que impulsa al cambio.
Una diferencia entre la solidificación y una transformación sólida, son los valores de la entalpía de cambio siendo menores en transformaciones sólidas que en el proceso de solidificación.
Esto nos lleva a determinar que las fuerzas conductoras en estado sólido son del orden de una
tercera parte de las de solidificación, lo cual es lógico si miramos la ecuación (4), el cambio de
entropía en una transformación solido-sólido es menor al producido en el cambio líquidosólido y por tanto también es menor ∆H/Te (Te = temperatura de equilibrio de fases).
=
79
Cinética del cambio de fase
3. NUCLEACIÓN HOMOGÉNEA
Como se ha indicado en la introducción, las transformaciones con difusión como el
crecimiento de un metal a partir del líquido durante la solidificación, o el crecimiento de una
fase sólida a expensas de otra durante una transformación en estado sólido, necesita un mecanismo mediante el cual los átomos se van depositando sobre la superficie del cristal que está
creciendo. Esto significa que la transformación con difusión solamente puede tener lugar si
cristales de la nueva fase están ya presentes, lo que implica que el proceso comienza con la
formación de pequeñas partículas sólidas denominados núcleos.
La formación de núcleos se
debe al agrupamiento ordenado de
algunos átomos, que al disminuir la
temperatura, consiguen ser termodinámicamente estables dentro de
la masa líquida, en caso contrario
estas agrupaciones son destruidas
por las fluctuaciones térmicas del
líquido.
Estos núcleos al solidificar Figura. 3
actúan como centros para posteriores cristalizaciones. A medida que aumenta el enfriamiento hay más átomos que se va uniendo
a los núcleos estables aumentando el tamaño de estos. A veces los subenfriamientos necesarios
para la formación de núcleos son muy grandes, pudiendo ser incluso de varios cientos de grados.
Consideremos un volumen líquido a una temperatura ∆T inferior a la de equilibrio Tm,
figura 3, con una energía libre G1. Si se forma un pequeño núcleo sólido en la masa líquida, la
energía libre del sistema habrá variado siendo ahora G2. Esta energía dependerá de la del propio líquido restante, de la del sólido formado y de la propia interfase sólido-líquido. Es decir
G2 será:
G 2 = V s G s + V L G L + AsL γ sL
(7)
donde Vs es el volumen del sólido, VL el del líquido, AsL la superficie de la interfase sóli-
80
Cinética del cambio de fase
do/líquido, Gs y GL las energías por unidad de volumen del sólido y líquido respectivamente y
γsL la energía libre de la interfase. La energía libre del sistema sin ningún sólido, teniendo en
cuenta que el volumen en este caso será Vs+VL, para utilizar la misma nomenclatura, será:
G1 = ( V s + V L ) G L
(8)
Como resultado de la formación del sólido se produce un cambio en la energía libre del
sistema que vendrá dada como ∆G21= G2 - G1, de donde:
∆ G 21 = - V s ∆G + AsL γ sL
(9)
donde: ∆G=GL-GS
Para un subenfriamiento ∆T según la ecuación (6) ∆G es positivo, por lo que la energía
libre asociada al cambio, con la formación de pequeños volúmenes de sólido disminuye la
energía del sistema, dado que la energía del sólido formado es menor que la energía que tenía
el líquido que ocupaba ese mismo volumen. Sin embargo también existe un aumento de energía debido a la creación de la interfase sólido/líquido, luego el aumento o disminución de
energía debido a la formación de una partícula de sólido, dependerá de la influencia y de la
forma en que varíen estos dos términos. Suponiendo que la partícula de sólido es esférica la
expresión (9) se podría poner:
4
3
∆ G r = - π r 3 ∆G + 4π r 2 γ sL
(10)
Representando gráficamente cada término de la ecuación anterior se observa, figura 4,
que existe un tamaño crítico de núcleo a partir del cual la energía del sistema disminuye. Nótese que la energía libre disminuye con r3, mientras que el incremento de energía interfacial lo
hace con r2, para r inferiores al crítico domina el termino de energía superficial incrementándose ∆G con r,
por el contrario para r mayor que r*
domina el termino de volumen disminuyendo la energía con r. La creación, por tanto, de partículas muy
pequeñas siempre produce un incremento de energía total del sistema, fig. 4. Este incremento es capaz
de mantener el metal líquido a temperaturas inferiores a Tm casi indefinidamente. También se puede deduFigura. 4
81
Cinética del cambio de fase
cir de la figura, que para poderse formar un sólido a partir de un líquido fundido, por enfriamiento, es necesario salvar un umbral energético. Debido a las fluctuaciones térmicas, es posible que en algunos puntos del sistema en algún momento, se hayan podido formar agrupaciones atómicas con un tamaño suficiente para que puedan comenzar a crecer.
De la figura 4 se puede observar que para radios de partículas sólidas r < r* la energía
disminuye si el sólido se redisuelve en el líquido, para r > r* por el contrario la energía disminuye si aumenta el tamaño del sólido. Agrupaciones atómicas con tamaños menores que el crítico son conocidos como embriones, estos son inestables, estando por tanto formándose y destruyéndose constantemente, tamaños superiores se conocen como núcleos, para r = r* es el tamaño de núcleo crítico a partir del cual comienza la solidificación haciéndose estables las pequeñas agrupaciones formadas en el seno del líquido. El valor de r* se puede determinar matemáticamente considerando que existe un máximo en la curva de ∆G, por tanto para r=r*,
dG=0, derivando por tanto la ecuación (10) y operando se obtiene:
*
r =
2 γ sL
∆G
(11)
y sustituyendo la ecuación (11) en la (10) se obtiene:
∆ G* =
16π γ 3sL
3( ∆G )2
(12)
sustituyendo ∆G de la ecuación (6) en las expresiones anteriores, se obtiene:
*
r =
2 γ sL T m 1
L
∆T
16π γ 3sL T 2m 1
∆G =
3 L2
∆T2
*
(13)
(14)
De las ecuaciones anteriores se puede ver que r* y ∆G* disminuyen con el grado de
subenfriamiento ∆T. Como consecuencia, a medida que la solidificación se realiza a temperaturas más bajas, menor será el tamaño de la partícula crítica y más posibilidades habrá de que
se formen y en más puntos del líquido. Debido a la existencia de una barrera energética para la
formación de un núcleo, será necesario proporcionar energía al sistema de alguna manera para
la iniciación del proceso, esta energía se suministra en forma de fluctuaciones de la energía
térmica. La nucleación comienza cuando ∆G* es inferior a un cierto valor crítico de ≅ 55 kTm,
lo que quiere decir que se necesita un grado de subenfriamiento determinado para disminuir
∆G* a valores próximos o inferiores a 55 kTm.
82
Cinética del cambio de fase
4. NUCLEACIÓN HETEROGÉNEA
La nucleación homogénea rara vez se presenta en la práctica, en lugar de ello las impurezas que están en contacto con el líquido, en suspensión o en las paredes, proporcionan un
punto de inicio de la nucleación favoreciendo la formación de núcleos y de esta manera el inicio de la solidificación. Este tipo de nucleación se denomina heterogénea.
Antes de entrar en el desarrollo termodinámico de este proceso, analicemos brevemente la ecuación (14). Se puede ver que si la nucleación se produce con subenfriamientos pequeños, para que el umbral energético ∆G* sea suficientemente bajo para que se pueda iniciar
la nucleación, es necesario que
disminuya el termino de energía
interfacial, dado que el resto de
términos que aparecen en la ecuación son constantes. Una forma
de conseguirlo es mediante la nucleación heterogénea. Consideremos un sólido formándose en la
pared del molde, como se muestra
en la figura 5. En este caso la
variación de energía libre que se
produce es debida no solo al volumen y superficie del sólido
formado, sino también a la variaFigura. 5
ción de la energía superficial del
molde, por ser distintas la energías superficiales molde-sólido (γSM) que molde-líquido (γML). Teniendo en cuenta estos términos y que el ángulo θ es aquel que satisface el equilibrio de fuerzas debido a las tensiones superficiales en los bordes de la nueva partícula ( γ ML = γ SM + γ SL cosθ ), y haciendo las mismas
consideraciones que en el caso anterior se obtiene :
4
3
∆ G het = - π r 3 ∆G + 4π r 2 γ sL S( θ )
(15)
83
Cinética del cambio de fase
esta expresión es igual a la ecuación (10) excepto por el termino S(θ )=(1/23/4cosθ+1/4cos3θ ), función del ángulo
húmedo formado por el núcleo sobre la pared y siempre es menor que 1. De ésta expresión se puede observar que la barrera de
energía de activación es más pequeña que en
el caso anterior, Fig. 6. Con un mismo subenfriamiento hay un menor incremento de la
energía superficial, luego, al contrario para
una misma barrera de energía es necesario un
menor subenfriamiento, Fig. 7.
Además téngase en cuenta que para un radio
determinado el número de átomos que se necesitan para formar una partícula sólida es mucho menor, Fig. 5.
Figura. 6
En la práctica se añaden algunas veces impurezas al líquido para que actúen como centros de nucleación. Estas, forman compuestos entre ellas o con algún componente fundido,
formando partículas sobre las que se inicia un núcleo. Al tener un gran número de centros de
nucleación se produce un afino de grano. Esta práctica se denomina inoculado. Para que las
impurezas tengan efecto sobre una masa fundida es necesario que los elementos añadidos o los
compuestos formados tengan temperaturas de fusión más altas que el líquido para que al al-
Figura. 7
84
Cinética del cambio de fase
canzar la temperatura de fusión de este último las impurezas estén en estado sólido y pueden
cumplir con su cometido.
5. VELOCIDAD DE NUCLEACIÓN
Para conocer el desarrollo del proceso es importante conocer o estimar a que velocidad
se formarán los núcleos y con que rapidez se van a desarrollar. Para determinar el número de
núcleos que existen en el sistema a una temperatura determinada, se puede hacer un planteamiento equivalente al realizado en la obtención de defectos en equilibrio, dado que es un proceso similar. La formación de un núcleo necesita de una energía de activación y su formación,
además, disminuye la energía del sistema, considerando por tanto que la energía de activación
para la formación de un núcleo es ∆G*, la expresión final será:
*
n = n0 exp -
∆ G*
kT
(16)
donde no es el número de átomos por unidad de volumen que existe en el líquido.
La expresión anterior nos dice el número de posible de agrupaciones con el tamaño crítico, sin embargo no comenzará el proceso de cambio hasta que algún núcleo capte un átomo
suplementario, es decir: primero se tiene que vencer la barrera ∆G*, lo que lleva asociado cambios de energía superficial a la formación del núcleo, y posteriormente estos núcleos tienen que
estar en disposición de crecer.
En resumen, existe el hecho de
que los átomos se difunden y se
reagrupan para formar un núcleo. La velocidad de nucleación, N, dependerá por tanto no
sólo del número de núcleos con
suficiente energía para ser estables, sino también de la facilidad para difundirse y formar el
núcleo. Este segundo factor depende del coeficiente de difusión D. La variación de la difusividad con la temperatura depende mucho del tipo de mate- Figura. 8
85
Cinética del cambio de fase
rial, así en los vidrios y polímeros D disminuye fuertemente con la temperatura, sin embargo
en los metales estas variaciones son pequeñas, a no ser que se produzcan enfriamientos a temperaturas muy bajas para la obtención de metales amorfos. Este distinto comportamiento del
coeficiente de difusión influirá en la velocidad de nucleación de cada tipo de material. Por tanto la velocidad de nucleación N podrá expresarse como:
N∝
D
∆ G*
exp Dm
kT
(17)
donde Dm es el coeficiente de difusión a la temperatura de solidificación y D a la temperatura
de subenfriamiento.
En la nucleación heterogénea, la velocidad de formación de núcleos sigue un proceso
similar al de la nucleación homogénea, la expresión es similar a la anterior incluyendo simplemente el término del ángulo húmedo. En la figura 8 se muestran las curvas de velocidad de
nucleación para los dos tipos, homogénea y heterogénea.
A temperaturas próximas a la de transformación, la difusión (capacidad de movimiento
de los átomos) es grande, sin embargo ∆G* es grande y por tanto muy pocos átomos tendrán
suficiente energía para vencer la barrera energética y alcanzar el tamaño crítico. Con subenfriamientos muy grandes ocurre lo contrario, ∆G* es muy pequeño, pero los átomos no tienen
apenas capacidad de movimiento para formar núcleos, la velocidad de nucleación es también
baja. A subenfriamientos intermedios, por tanto, donde la difusión es todavía alta y ∆G* no es
demasiado grande, debe de existir un máximo en la velocidad de nucleación. Este máximo
puede ocurrir a temperaturas muy por debajo de la de transformación. Esta forma de campana
de la curva de velocidad de nucleación solo es válida para materiales en los que la relación
D/Dm disminuya de forma importante con la temperatura, es decir para materiales viscosos no
metálicos (polímeros, vidrios, óxidos, etc.). Para la solidificación de materiales metálicos esta
curva tiene forma exponencial, ya que para las temperaturas de enfriamiento habituales utilizadas en los procesos industriales la relación D/Dm es prácticamente constante e igual a la unidad
y el proceso está controlado por el flujo de calor. En las transformaciones en estado sólido la
variación del coeficiente de difusión con la temperatura es también importante y la velocidad
de nucleación sigue un modelo de forma de campana. En estas transformaciones el movimiento de la interfase es la que controla el proceso siendo la difusión el mecanismo principal de
control.
86
Cinética del cambio de fase
6. NUCLEACIÓN EN SÓLIDOS
La nucleación en los sólidos es muy
parecida a la nucleación en líquidos. Debido
a la existencia de defectos de alta energía,
cómo límites de grano, dislocaciones, etc.
las nuevas fases que se forman en los procesos de transformación en estado sólido
son nucleadas de forma heterogénea a partir
de éstas zonas de más alta energía. La formación de las nuevas fases se producen
fundamentalmente en el centro y límites de
grano. La teoría de la transformación en esFigura 9
tos casos es la misma que se ha visto para el
caso de solidificación, habría que tener en cuenta sin embargo, la variación de energía por eliminación de fronteras de grano y el aumento de energía de deformación producido por la formación de la nueva fase. En la figura 9, se muestra cuales podrían ser las zonas potenciales de
formación de las nuevas estructuras.
La forma de los granos será que la que proporcione el estado de mínima energía y dependerá de la relación entre las energías superficiales entre fases, igual que se vio en la nuclea-
Figura 10
87
Cinética del cambio de fase
ción heterogénea. La forma en que se producen las uniones entre las intercaras de las fases,
tiene gran importancia por las deformaciones que pueden producirse en la red y su consecuencia en el comportamiento mecánico del material. Estas uniones pueden ser coherentes, semicoherentes e incoherentes, según que las fases traten de mantener la misma estructura en las
dos direcciones del plano de unión, solo la sigan en una dirección o no la sigan en ninguna, en
la figura 10 se muestran cómo pueden ser estas uniones entre granos.
7. CRECIMIENTO
Una vez formado el núcleo, comienza su crecimiento en las tres direcciones del espacio, añadiéndose nuevos átomos al cristal que comienza su formación. Este proceso se realiza
mediante difusión. La unión de nuevos átomos a la red no se realiza en todas las direcciones
por igual, sino en determinadas direcciones preferentes.
El crecimiento continúa hasta interferir con otro cristal que a su vez esta creciendo en
otra dirección. La solidificación tiene por tanto dos etapas, por un lado la formación de núcleos, y por otro el crecimiento de estos.
El crecimiento está condicionado por la
forma y la velocidad a la que se extrae el calor a
través de la interfase sólido-líquido, dos tipos de
calor han de extraerse, el calor específico y el
calor latente de transformación. El calor específico es el calor almacenado debido al nivel térmico, la evacuación del calor se realiza por conducción a través del sólido o del líquido según
sea el gradiente térmico en la interfase. Este calor se elimina por conducción a través del sólido
o por convección en el líquido. El desprendimiento de este calor hace que la interfase se caliente acercándose la temperatura a Tm. La velocidad a la que los núcleos puedan crecer, también depende de la movilidad de los átomos en
la interfase sólido-líquido, es decir del coeficien- Figura. 11
te de difusión.
88
Cinética del cambio de fase
Aunque no es fácil obtener una expresión para obtener la velocidad de crecimiento de
los núcleos debido al carácter direccional de la solidificación y a la influencia de otros muchos
factores se puede hacer un planteamiento similar al visto en el apartado anterior. La cinética
del crecimiento está condicionada fundamentalmente por la difusión, es decir por la capacidad
de movimiento de los átomos que les permita añadirse a los núcleos existentes y permitirles su
crecimiento. También depende de la diferencia de energía libre asociada a la transformación
(fuerza conductora). A subenfriamientos pequeños la fuerza conductora es pequeña y por tanto
pequeña la velocidad de crecimiento. Con grandes subenfriamientos la difusión es pequeña
ocurriendo lo mismo que en el caso anterior. Lógicamente igual que con la velocidad de nucleación, debe de haber un máximo asociado a éste mecanismo, la variación con la temperatura tiene una forma similar a la velocidad de nucleación. El máximo de la curva de velocidad de
crecimiento está desplazada a temperaturas superiores con respecto al máximo de la curva de
velocidad de nucleación, Figura 11.
Las transformaciones que ocurren a temperaturas próximas a la de fusión, según la figura anterior, tienen baja velocidad de nucleación y alta de crecimiento, luego la microestructura final será de granos grandes, comienza la formación del sólido en pocos lugares y crecen
muy rápidamente. Las solidificaciones con grandes subenfriamientos tienen velocidades de
formación de núcleos altas que crecen de manera moderada, por lo que formarán un sólido con
muchos granos y por tanto de pequeño tamaño. Lo anterior es considerando una transformación isotérmica, si la solidificación se produce con enfriamiento continuo, un enfriamiento lento favorece las transformaciones a altas temperaturas dando lugar a la formación de un grano
basto. Grandes velocidades de enfriamiento, no dan tiempo a que ocurran las transformaciones
a altas temperaturas, solidificando con grandes subenfriamientos y dando lugar a una estructura de grano fino.
89