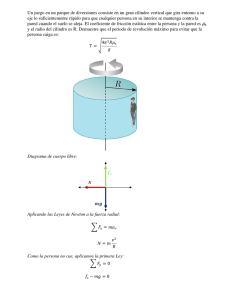
EJEMPLO: Hallar las dimensiones de una lata común de refresco
Anuncio

EJEMPLO: Hallar las dimensiones de una lata común de refresco de forma cilíndrica, de 350 ml, que llevará la cantidad mínima de metal. Sea: r = el radio de la base h = altura del cilindro El área de la base es r2 igual al área de la tapa. El área lateral es 2rh, producto de la circunferencia por la altura del cilindro. Por lo tanto, el área total (AT), que es la función a minimizar, está dada por: fAT: f(r,h) = 2rh + 2r2 El otro dato del problema es el volumen del cilindro (r2h), que debe ser igual a 350 ml. De este se despeja la altura, para sustituir en la función área total. r2h = 350 f AT f´ h 2 : f( r ) 700 2r r AT : f´( r ) 700 4r 2 r 350 2 r f : f( r ) 2 r 350 AT 2 r se deriva con respecto a r f´ AT 3 que se anula en: Que es un mínimo de la función. La altura es: r3 : f´( r ) 700 4 2r 2 700 4r 2 r 3.82 cm El símbolo significa aproximadamente igual. h 7.63 cm Las dimensiones de la lata cilíndrica de 350 ml que tiene menos superficie lateral son: una base de aproximadamente 3.82 cm de radio y una altura de aproximadamente 7.63 cm. NOTA En general, para cualquier volumen se cumplirá que el cilindro de menor área total es aquel que tiene iguales su altura y el diámetro de la base. La demostración del caso general puede hacerla el estudiante.