modo o acción del controlador

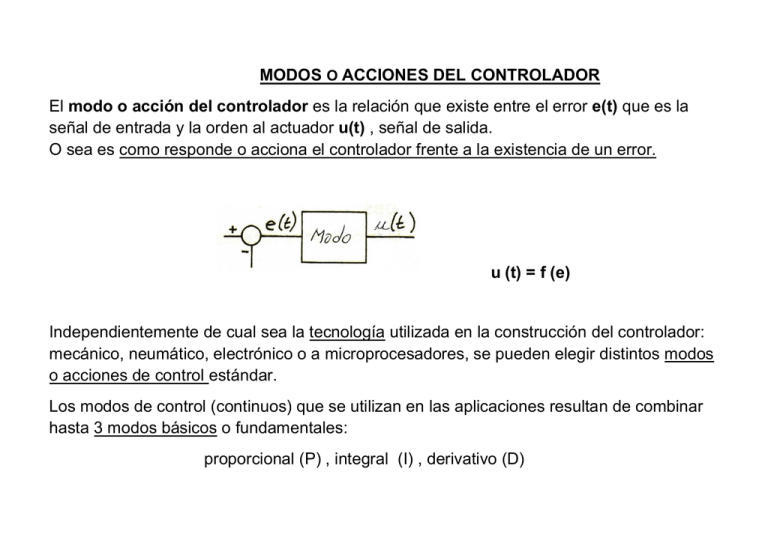
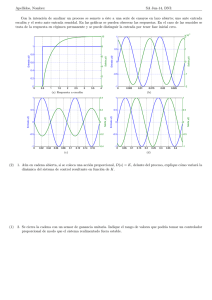
MODOS O ACCIONES DEL CONTROLADOR
El modo o acción del controlador es la relación que existe entre el error e(t) que es la
señal de entrada y la orden al actuador u(t) , señal de salida.
O sea es como responde o acciona el controlador frente a la existencia de un error.
u (t) = f (e)
Independientemente de cual sea la tecnología utilizada en la construcción del controlador:
mecánico, neumático, electrónico o a microprocesadores, se pueden elegir distintos modos
o acciones de control estándar.
Los modos de control (continuos) que se utilizan en las aplicaciones resultan de combinar
hasta 3 modos básicos o fundamentales:
proporcional (P) , integral (I) , derivativo (D)
a) MODO PROPORCIONAL (P): Salida al actuador proporcional al error y(t) = Kp .e
O sea es una acción de control proporcional a la desviación del valor medido de la variable
controlada respecto al punto de consigna.
b) MODO INTEGRAL (I) Salida al actuador proporcional a la integral del error (o sea al
error acumulado)
Para facilitar la suma cuando se usa el P+ I, se suele introducir el tiempo integral: Ti
definido por: Ki = Kp / Ti .
El modo I es una acción lenta que se va desarrollando con el transcurso del tiempo, como
se comprende si recordamos que la integral es el área bajo la curva e(t).
c) MODO DERIVATIVO (D) Salida proporcional a la derivada del error o sea proporcional
a la velocidad de variación del error.
Td: tiempo derivativo
La acción D se anula cuando el error alcanza un valor constante o estacionario.
Usualmente los controladores industriales usan los modos: P, P+I, P+D y P+I+D, y cada
uno tiene propiedades características:
1) La acción proporcional P sóla varía instantánea y simultáneamente con el error.
En particular alcanza un valor fijo o estacionario cuando el error es constante.
La acción proporcional presenta el problema del error en estado estacionario cuando hay
variaciones de carga. También se dice que produce un error de off-set.
EJEMPLO:
En el control de nivel por flotador y palanca de la fig. siguiente hay una acción de control
proporcional.
Partimos de una posición de equilibrio (estado estacionario) en que debe ser: Qin = Qout
siendo Qin y Qout caudales de entrada y salida, palanca horizontal y con el nivel en el valor
deseado “ho” (set point).
Si la carga (Qout caudal de salida) aumenta, entonces para alcanzar una nueva posición de
equilibrio (estado estacionario) tiene que aumentar la entrada (Qin) y para ello la apertura
de la válvula debe aumentar, y eso implica que el nuevo nivel de equilibrio “ h” debe estar
por debajo del inicial o valor deseado.
Esa diferencia de niveles es lo que se conoce como error de estado estacionario.
-------------------------------------------------------------------------------------------
En la expresión: u (t) = Kp .e el factor “Kp” se llama ganancia proporcional, (en la
bibliografía a veces aparece como: Kc)
Es un parámetro que se puede variar (ajuste del controlador) para mejorar la
respuesta del controlador.
En la fig. siguiente se muestra la variación temporal de la variable controlada (curvas a
color) después de un salto en escalón unitario en el punto de consigna (en negro) cuando
aumenta la ganancia del controlador Kp sucesivamente a valores: 2, 5, 10 y 15.
Se observa que al ir aumentando Kp :
1. El error en estado estacionario disminuye.
2. El proceso responde más rápidamente.
3. La sobre-oscilación (o sobre paso) y las oscilaciones aumentan.
2) Acción proporcional + integral: PI
La salida del controlador es:
La combinación: P+ I elimina el error de off-set. Esto es porque el modo I tiene en cuenta
la historia pasada del error y se estabiliza sólo cuando el error se hace cero
Cuando Ti crece el efecto de I disminuye, en el caso límite en que Ti tiende a (es) infinito
se acerca (corresponde) al control P sólo
Las propiedades de la acción integral se muestran en la fig. siguiente en la que se puede
ver la respuesta temporal de un controlador PI a un cambio en escalón del set-point.
La ganancia proporcional Kp se mantuvo constante y se varió sólo el tiempo integral.
Se observa que:
1. El error en estado estacionario se elimina.
2. Cuando Ti disminuye (mayor acción integral) la respuesta se hace cada vez más
oscilatoria, pudiendo en último término llegar a inestabilizar el sistema.
3) La acción proporcional + derivativa PD.
La salida del controlador es:
La acción D detecta la velocidad de cambio del error por lo que da al PD cierto carácter de
previsión: el modo PD es de acción rápida, de alta sensibilidad y produce una corrección
significativa antes que el error se vuelva muy grande (efecto de amortiguamiento).
La acción D no elimina el error de off-set, pero por su acción de amortiguamiento reduce el
sobre-pico lo que permite valores de Kp altos lo que disminuye el error de off-set como se
vio.
En la fig. sgte. se puede ver la simulación de un controlador PD con una entrada escalón.
Las oscilaciones se amortiguan a medida que Td aumenta la salida se va aproximando
cada vez más a una exponencial.
Un ejemplo de aplicación del PD puede ser en el control de temperatura: debido a la inercia
térmica del sistema es importante saber hacia dónde se está evolucionando. La acción de
calentamiento tiene que pararse a tiempo. Una conducción lenta de calor puede significar
que, incluso después de desconectar el sistema de calentamiento, la temperatura continúe
aumentando durante mucho tiempo y durante este período la temperatura puede
sobrepasar considerablemente su punto de consigna.
4) La combinación PID (proporcional + integral + derivativo) reúne las ventajas de los
tres modos.
La señal de salida es ahora:
Las tres constantes son independientes pueden ajustarse separadamente.
El controlador PID se puede representar con el siguiente diagrama de bloques con la
notación: Kc para la constante proporcional en vez de Kp, (o sea Kp = Kc) :
El ajuste o configuración de un controlador consiste en elegir o determinar: Kc, Ti y Td , y
ello se hace en función de las características de cada lazo particular y con el objetivo de
mejorar u optimizar la estabilidad, la velocidad de respuesta del sistema a la presencia de
perturbaciones(compensación de sus efectos) y al error de off-set.
La tabla siguiente da una idea de cómo varían la estabilidad, la velocidad y el error en
estado estacionario cuando se modifican los parámetros del controlador.
Esta tabla es sólo una referencia aproximada.
Kp aumenta
Ti disminuye
Td aumenta
Estabilidad
se reduce
disminuye
aumenta
Velocidad
aumenta
aumenta
aumenta
Error est. estacionario
no eliminado
eliminado
no eliminado
FUNCION DE TRANSFERENCIA DEL BLOQUE CONTROLADOR: PID
Para pasar al dominio de Laplace consideramos las variaciones respecto al estado
estacionario (de equilibrio):
Usando las propiedades de la T. de Laplace la función de transferencia del controlador PID
será: