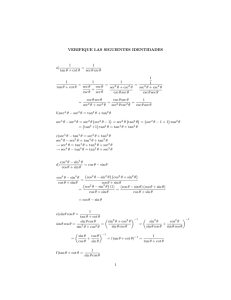
CHAPTER 7: INTEGRALS WE KNOW ∫ xn dx = 1 n + 1 xn+1 + C (n
Anuncio

CHAPTER 7: INTEGRALS WE KNOW Z Z Z Z Z Z Z Z Z Z Z Z Z xn dx = 1 xn+1 + C n+1 (n 6= −1) 1 dx = ln |x| + C x ex dx = ex + C cos(x) dx = sin(x) + C Z Z 1 1 dx = ln |ax + b| + C ax + b a 1 eax dx = eax + C a Z cos(ax) dx = Z 1 sin(ax) dx = − cos(ax) + C a 1 sin(ax) + C a sec2(x) dx = tan(x) + C sec(x) tan(x) dx = sec(x) + C sin(x) dx = − cos(x) + C csc2(x) dx = − cot(x) + C csc(x) cot(x) dx = − csc(x) + C 1 dx = tan−1(x) + C 2 1+x √ 1 dx = sin−1 (x) + C 1 − x2 tan(x) dx = ln | sec(x)| + C cot(x) dx = ln | sin(x)| + C
![1. ∫ [u(x)] u (x)dx = r + 1 + C, r = −1 2. ∫ u∨(x) u(x) dx = ln|u(x)| + C](http://s2.studylib.es/store/data/008568496_1-96765d9c7bd315d4a548949875995ddd-300x300.png)