INTERPRETACIÓN GEOMÉTRICA
Anuncio
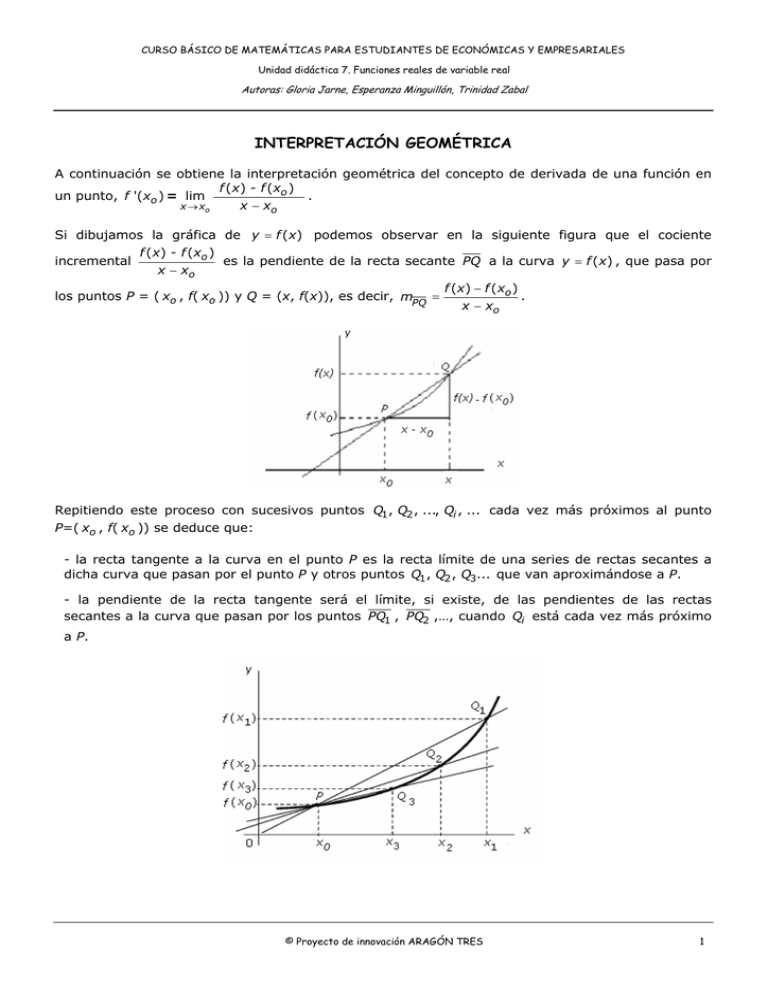
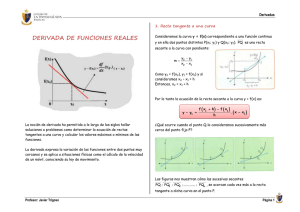
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES Unidad didáctica 7. Funciones reales de variable real Autoras: Gloria Jarne, Esperanza Minguillón, Trinidad Zabal INTERPRETACIÓN GEOMÉTRICA A continuación se obtiene la interpretación geométrica del concepto de derivada de una función en f ( x ) - f (xo ) . un punto, f '( xo ) = lim x − xo x → xo Si dibujamos la gráfica de y = f ( x ) podemos observar en la siguiente figura que el cociente f ( x ) - f (xo ) incremental es la pendiente de la recta secante PQ a la curva y = f ( x ) , que pasa por x − xo los puntos P = ( xo , f( xo )) y Q = (x, f(x)), es decir, mPQ = f (x ) − f (xo ) . x − xo Repitiendo este proceso con sucesivos puntos Q1, Q2 , ..., Qi , ... cada vez más próximos al punto P=( xo , f( xo )) se deduce que: - la recta tangente a la curva en el punto P es la recta límite de una series de rectas secantes a dicha curva que pasan por el punto P y otros puntos Q1 , Q2 , Q3... que van aproximándose a P. - la pendiente de la recta tangente será el límite, si existe, de las pendientes de las rectas secantes a la curva que pasan por los puntos PQ1 , PQ2 ,…, cuando Qi está cada vez más próximo a P. © Proyecto de innovación ARAGÓN TRES 1 CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES Unidad didáctica 7. Funciones reales de variable real Autoras: Gloria Jarne, Esperanza Minguillón, Trinidad Zabal Cuando x → xo , es decir, Qi → P , si existe lim mPQ = lim Qi → P i x → xo f ( x ) − f ( xo ) nos da la pendiente de la x − xo recta tangente a la curva y = f ( x ) en P. Por tanto, teniendo en cuenta que f '( xo ) = lim x → xo f ( x ) - f (xo ) , se concluye que la derivada de f en el x − xo punto xo es la pendiente a la recta tangente a la curva y = f ( x ) en P. La ecuación de la recta tangente a la curva y = f ( x ) en el punto xo , conocida su pendiente, se puede escribir de la forma: y − f ( xo ) = f '( xo )( x − xo ) Ejemplo 5: Hallar la pendiente y la ecuación de la recta tangente a la gráfica de f (x ) = x 2 − 1 en el punto x = 2. f ( x) − f (2) x2 − 1 − 3 x2 − 4 ( x − 2)( x + 2) = lim = lim = lim = lim (x + 2) = 4 x →2 x →2 x →2 x − 2 x →2 x →2 x −2 x −2 x −2 La pendiente es f '(2) = lim La ecuación de la recta tangente es y − f (2) = f '(2)(x − 2) , es decir, y − 3 = 4(x − 2) , y operando queda y = 4 x − 5 . © Proyecto de innovación ARAGÓN TRES 2