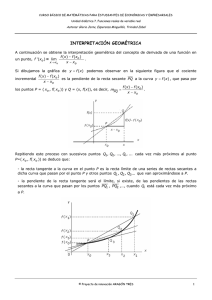
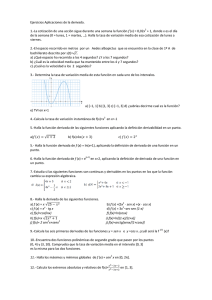
TALLER DE RECUPERACIÓN CÁLCULO LICEO CULTURAL L.E.O. Docente, Rubén Esteban Escobar Sánchez

TALLER DE RECUPERACIÓN
CÁLCULO
LICEO CULTURAL L.E.O.
Docente, Rubén Esteban Escobar Sánchez
La siguiente recuperación consta de tres momentos, en primera medida como requisito
debe presentarse el cuaderno totalmente al día para así, revisarse el taller propuesto que
debe ser presentado en hojas cuadriculadas, debidamente legajado en carpeta; luego de
la respectiva revisión del taller se llevará a cabo la sustentación del mismo ya sea en forma
oral o escrita, y ésta determina la valoración definitiva.
1. Representa gráficamente cada una de las siguientes funciones:
a) f(x) = x
c) f(x) = 2x -1
𝑥
e) f(x) = 2
g) f(x) =
b) f(x) = 3x + 1
d) f(x) = 2x
f) f(x) = -x
−𝑥+2
3
h) f(x) = 3x – 1
2. Cuando se toma en arriendo un apartamento se paga por anticipado el primer mes. Si el
valor del arriendo de un apartamento es de $700000 mensuales, halla:
a) La ecuación que relaciona la variable costo (C) con la variable meses.
b) El valor pagado por el arrendatario si han transcurrido:
6 meses
1 mes
ningún mes
quince días
3. Sean f(x) = x2; g(x) = x + 1; h(x) = 3(x + 1), halla:
𝑓+𝑔
a) ( ℎ ) (𝑥)
b) ( f o g o h) (x)
c) f * [𝑔 𝑜 ℎ] (𝑥)
4. Escribe los primeros 12 términos de las siguientes sucesiones:
1
a) an = 1 - 2𝑛
b) an =
√𝑛+1
𝑛
1
c) an = (-1)n + 13𝑛−1
𝑛!
d) an = 3𝑛∗5𝑛−1
5. Determina el límite en cada uno de los siguientes ejercicios, y construye la grafica:
𝑥2− 4
𝑥→2 𝑥−2
a) lim
𝑥2− 𝑡2
𝑥→−𝑡 𝑥+𝑡
c) lim
(3𝑢+4)(2𝑢−2)3
(𝑢−1)2
𝑢→1
e) lim
𝑥 3 − 4𝑥 2 + 𝑥+6
𝑥+1
𝑥→−1
b) lim
𝑥 4 − 18𝑥 2 + 81
(𝑥−3)2
𝑥→3
d) lim
𝑥 4 + 2𝑥 3 − 𝑥 2
𝑥2
𝑥→0
f) lim
6. Considere:
y=x2+1
a) Haga el bosquejo de su gráfica tan detallado como sea posible.
b) Dibuje la recta tangente en (1,2)
c) Calcule la recta tangente que pasa por (1,2)
y=x3-1
a) Haga el bosquejo de su gráfica tan detallado como sea posible.
b) Dibuje la recta tangente en (2,7)
c) Calcule la recta tangente que pasa por (1,2)
7. Encuentre las pendientes de las rectas tangentes a la función dada y construya su
gráfica teniendo en cuenta cada uno de los puntos dados:
a) y = x2 – 1 en los puntos en donde x = -2, -1, 0, 1, 2
b) y = x3 – 3x en los puntos en donde x = -2, -1, 0, 1, 2
8. En cada una de las siguientes funciones, halla la derivada mediante el concepto de
límite:
a) f(x) = x3 + 2x2 + 1
b) f(x) = x2 + x + 1
c) f(x) = 5x2 + 4x - 3
d) f(x) = x2 – 8x + 4
9. Aplicando el concepto de incremento relativo de una función, calcula la derivada de
cada una de las funciones dadas:
a) f(x) = x
b) f(x) = 6x2 + 4x + 1
c) f(x) = x2 – 6x + 1
1
d) f(x) = 3 𝑥 3 +
𝑥2
2
− 𝑥+5
10. Halla la derivada de las siguientes funciones utilizando el método más apropiado:
𝑥+1 3
a) y = (𝑥−1)
b) y = (2 − 3𝑥 2 )4 (𝑥 7 + 3)3
2𝑥−3
c) y = (𝑥 2+ 4)2
d) y = (4 + 2𝑥 2 )7
11. Halla la integral en cada unos de los ejercicios del numeral 8 y 9.
12. Elabora un breve resumen con ejemplos (4) y gráficas si es necesario, sobre los
siguientes temas, ayúdate con textos, apuntes del cuaderno o consulta en internet:
a. Trazado e interpretación, transformación, simetría, y clasificación de gráficas.
b. Tipos de funciones.
c. Álgebra de funciones.
d. Sucesiones.
e. Límites.
f. Derivación.
g. Integración.