Estructuras de barras biarticuladas con cargas en el tramo.
Anuncio
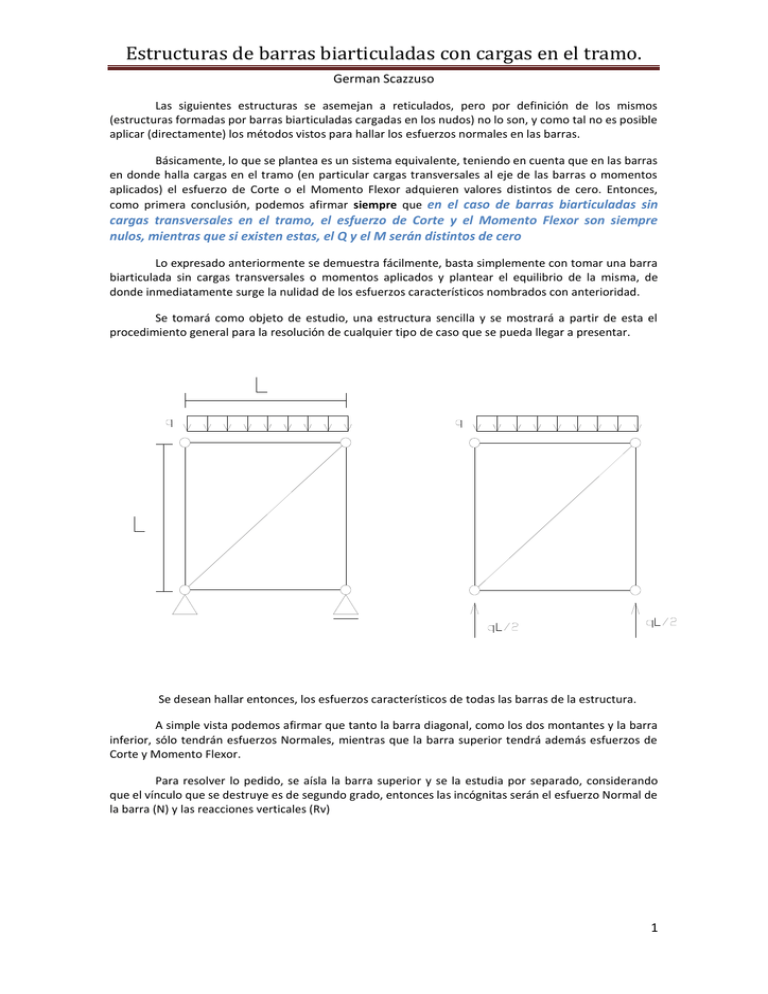
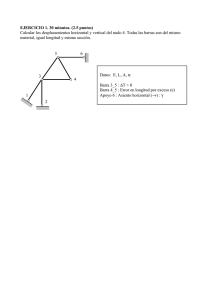
Estructuras de barras biarticuladas con cargas en el tramo. German Scazzuso Las siguientes estructuras se asemejan a reticulados, pero por definición de los mismos (estructuras formadas por barras biarticuladas cargadas en los nudos) no lo son, y como tal no es posible aplicar (directamente) los métodos vistos para hallar los esfuerzos normales en las barras. Básicamente, lo que se plantea es un sistema equivalente, teniendo en cuenta que en las barras en donde halla cargas en el tramo (en particular cargas transversales al eje de las barras o momentos aplicados) el esfuerzo de Corte o el Momento Flexor adquieren valores distintos de cero. Entonces, como primera conclusión, podemos afirmar siempre que en el caso de barras biarticuladas sin cargas transversales en el tramo, el esfuerzo de Corte y el Momento Flexor son siempre nulos, mientras que si existen estas, el Q y el M serán distintos de cero Lo expresado anteriormente se demuestra fácilmente, basta simplemente con tomar una barra biarticulada sin cargas transversales o momentos aplicados y plantear el equilibrio de la misma, de donde inmediatamente surge la nulidad de los esfuerzos característicos nombrados con anterioridad. Se tomará como objeto de estudio, una estructura sencilla y se mostrará a partir de esta el procedimiento general para la resolución de cualquier tipo de caso que se pueda llegar a presentar. Se desean hallar entonces, los esfuerzos característicos de todas las barras de la estructura. A simple vista podemos afirmar que tanto la barra diagonal, como los dos montantes y la barra inferior, sólo tendrán esfuerzos Normales, mientras que la barra superior tendrá además esfuerzos de Corte y Momento Flexor. Para resolver lo pedido, se aísla la barra superior y se la estudia por separado, considerando que el vínculo que se destruye es de segundo grado, entonces las incógnitas serán el esfuerzo Normal de la barra (N) y las reacciones verticales (Rv) 1 Estructuras de barras biarticuladas con cargas en el tramo. German Scazzuso Del equilibrio surge que: Con lo hallado, ya estamos en condiciones de trazar los diagramas de características de Corte y Momento Flexor, ya que el diagrama de la barra aislada es simple y expeditivo (barra simplemente apoyada con carga distribuida uniforme) y el resto de las barras poseen Q y M nulo. Diagrama de Esfuerzo de Corte 2 Estructuras de barras biarticuladas con cargas en el tramo. German Scazzuso Diagrama de Momento Flexor Lo único que resta es hallar los esfuerzos Normales. Basta únicamente analizar de nuevo la barra seccionada: Los esfuerzos que se calcularon en la barra no son otra cosa que los esfuerzos en los nudos de la estructura de signo contrario, conclusión bastante obvia teniendo en cuenta el Principio de Acción y Reacción. Entonces, para calcular los esfuerzos Normales, se considera la siguiente estructura que SÍ es reticulado y con lo cual podemos aplicar cualquier método visto. 3 Estructuras de barras biarticuladas con cargas en el tramo. German Scazzuso Se deja como ejercicio, plantear el caso de una barra cargada con un Momento y con una carga distribuida lineal. 4