Examen Febrero 2006

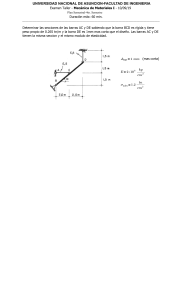
EJERCICIO 1. 30 minutos. (2.5 puntos)
Calcular los desplazamientos horizontal y vertical del nudo 4. Todas las barras son del mismo
material, igual longitud y misma sección.
5
3
6
4
Datos: E, L, A, α
Barra 3_5 : ∆T > 0
Barra 4_5 : Error en longitud por exceso (e)
Apoyo 6 : Asiento horizontal (→) : γ
1
2
EJERCICIO 2. 70 MINUTOS (3 puntos)
La estructura de la figura se realiza con un marco en forma de hexágono regular reforzado con tres
barras que unen todas sus esquinas para reforzarlo. Esta estructura se muestra a continuación.
q
A
P
B
P
F
C
L
E
D
q
Se trata de plantear su resolución aplicando el método matricial. Para ello, se pide:
a) Supuesto que las barras de la estructura no fuesen iguales, ¿crees que tendrías alguna
dificultad en aplicar el método matricial para resolverla? En caso afirmativo propón una
solución a esta dificultad.
El diseño definitivo será el siguiente; el marco estará realizado con perfiles HEB 240 y las barras de
refuerzo con perfiles IPN 300, los perfiles estarán orientados de tal forma que aprovechemos el
máximo momento de inercia en el plano de la estructura.
a) Dibuja y numera los grados de libertad para resolver el problema por el método matricial.
b) Escribe en función de q y P los vectores FN y Femp y el vector de desplazamientos, todos ellos
en coordenadas globales.
c) Realiza el ensamblaje gráfico de la matriz de rigidez global de la estructura. Utiliza para ellos
colores o rallados suficientemente distintivos e indica claramente a que barra pertenece cada
uno de ellos.
d) Indica cual es la matriz reducida que utilizarías para obtener los desplazamientos.
e) De la matriz anterior y utilizando el Sistema Internacional y sus múltiplos, indica el valor
numérico de los términos de la matriz global de la estructura que relacionan:
•
•
•
El desplazamiento horizontal de A con la fuerza en la misma dirección.[JPG1]
El giro de A con la fuerza horizontal en F.[JPG2]
El desplazamiento horizontal de F con el momento en A.[JPG3]
Una vez resuelta la estructura, con P=500 kN y q=100 kN/m, los desplazamientos en los extremos de
la barra AB en globales, valen:
A: u1 = 1.149 mm; u2 = -0.225 mm; u3 = -1.666 mrad.
B: u1 = -1.149 mm; u2 = -0.225 mm; u3 = 1.666 mrad.
Se pide:
f) Esfuerzos que soporta la barra AB.
g) Representación de las leyes de variación de los esfuerzos en AB, acotando los valores más
característicos y sus signos.