El suministro de agua potable a una población se realiza por

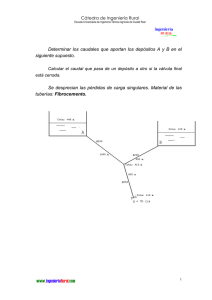
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
El suministro de agua potable a una población se realiza por
gravedad desde dos depósitos A y B conectados mediante tuberías de
fibrocemento según el esquema de la figura.
Calcular el caudal máximo que tendremos en el punto de entronque
con la población C, sabiendo que la presión requerida en dicho punto es de
2 atmósferas. Calcular cómo colabora cada depósito en el sistema.
Se suponen las pérdidas de carga accidentales un 15% de las
continuas.
La cota piezométrica es única (cada punto tiene UNA presión), luego
en D tienen que converger las líneas piezométricas trazadas desde los
depósitos A y B.
∇40
L.c.e.
A
L.c.e.
∇35
hAD
L.p.
hBD
B
10 m
5m
x
hDC
∇30 D
Pc/γ=20 mca
C ∇8
QDC = QAD + QBD
Q = 48.3 ⋅ D 2.68 ⋅ J0.56
(Scimemi, fibrocemento)
Observamos en la figura que:
1
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
hAD + x = 10
hBD + x = 5
hDC + 20 + 8 = x + 30 ⇒ hDC = x + 2
hT
, luego:
a ⋅L
10 - x
0.56
=
⇒ Q AD = 48.3 ⋅ D 2.68
AD ⋅ J AD
1.15 ⋅ 1160
5- x
2.68
0.56
=
⇒ QBD = 48.3 ⋅ DBD
⋅ JBD
1.15 ⋅ 700
(1)
2+ x
2.68
0.56
⇒ Q DC = 48.3 ⋅ DDC
⋅ JDC
1.15 ⋅ 500
(3)
Como hT = a⋅J⋅L, entonces J =
hAD = 10 – x ⇒ J AD
hBD = 5 – x
⇒ JBD
hDC = x + 2
⇒ JDC =
(2)
El problema se resuelve por tanteos, partiendo de que la presión en
D,
PD
, que hemos llamado “x”, estará comprendida entre 0 (salida libre en
γ
D) y 5 (el depósito B no aporta caudal).
0<x<5
Hacemos un primer tanteo suponiendo x = 2.5 m, y sustituimos este
valor en las ecuaciones (1), (2) y (3). De este modo se obtiene:
JAD = 5.62⋅10-3 0/1 ⇒ QAD = 3.55⋅10-2 m3/s
JBD = 3.11⋅10-3 0/1 ⇒ QBD = 1.78⋅10-2 m3/s
JDC = 7.83⋅10-3 0/1 ⇒ QDC = 7.78⋅10-2 m3/s
Comprobamos si QAD + QBD ≈ QDC
QAD + QBD = 5.33⋅10-2 < 7.78⋅10-2 = QDC
2
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
El caudal que aporta cada depósito debe aumentar, lo que conlleva
un aumento de las pérdidas de carga (puesto que están positivamente
P
relacionados), y en consecuencia, D debe ser menor.
γ
Después de varios tanteos se obtiene x = 1.05 mca. En efecto, para
este valor de x, QAD + QBD ≈ QDC.
JAD = 6.71⋅10-3 0/1 ⇒ QAD = 3.92⋅10-2 m3/s
JBD = 4.91⋅10-3 0/1 ⇒ QBD = 2.30⋅10-2 m3/s
JDC = 5.30⋅10-3 0/1 ⇒ QDC = 6.25⋅10-2 m3/s
Solución: El depósito A aporta 39.2 l/s y el depósito B, 23 l/s. En
estas condiciones, la presión residual en la población (C) será la requerida,
como podemos comprobar:
P
PD
+ z D = C + z C + hDC
γ
γ
hDC = a⋅JDC⋅LDC = 1.15⋅5.30⋅10-3⋅500 = 3.05 mca
x=
PC PD
=
+ z D − z C − hDC = 1.05 + 30 − 8 − 3.05
γ
γ
PC
= 20 mca
γ
3