"Rigidez de los Salarios Reales y NAWRUs Regionales: Evidencia
Anuncio

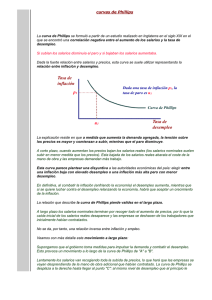
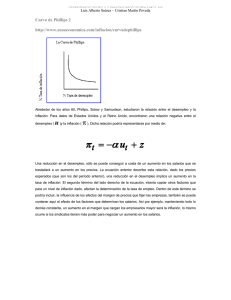
Documento de trabajo E2004/88 Curvas de Phillips y NAWRUs regionales: Evidencia empírica para la economía española Javier Capo Parrilla Francisco Gómez García Centro de Estudios Andaluces Documento de Trabajo Serie Economía E2004/88 Curvas de Phillips y NAWRUs regionales: Evidencia empírica para la economía española* JAVIER CAPÓ PARRILLA Universitat de les Illes Balears y CRE FRANCISCO GÓMEZ GARCÍA Universidad de Sevilla y Centro de Estudios Andaluces RESUMEN En este trabajo proporcionamos estimaciones de las NAWRUs (Tasa de Desempleo no Aceleradora de los Salarios) regionales de la economía española para el periodo 1989-2000. Hemos utilizado el método de Elmeskov, ampliamente implementado en la última década -por ejemplo en el marco del FMI y la OCDE- con el objetivo de obtener una "time-varying" NAWRU. Estas estimaciones nos permiten introducir el desempleo cíclico como argumento de las curvas de Phillips para las distintas Comunidades Autónomas. Los resultados obtenidos no reflejan la esperada relación negativa entre inflación salarial y desempleo. Palabras clave: NAWRU, histéresis, curva de Phillips, mercados de trabajo regionales. ABSTRACT This paper examines the existing differences between regional NAWRUs (Non Accelerating Wage Rate of Unemployment) in Spain for the period 1989-2000. Elmeskov’s methodology has been used. Regional time-varying NAWRUs are used to calculate cyclical unemployment which allows us to estimate Phillips curves for the Spanish regions. The results do not show the expected negative wage inflation-unemployment trade-off. Keywords: NAWRU, hysteresis, Phillips curve, regional labour markets. JEL classification: J30 y R23. Agradecemos los comentarios de Carlos Usabiaga a una versión preliminar de este trabajo y las sugerencias recibidas por parte de muchos colegas en el VII Encuentro de Economía Aplicada, especialmente de Juan F. Jimeno. Asimismo, este texto se ha beneficiado de los comentarios y sugerencias de un evaluador anónimo. Los errores que persistan son de nuestra exclusiva responsabilidad. * Centro de Estudios Andaluces 1. INTRODUCCIÓN No cabe duda de que uno de los principales problemas al que se han enfrentado la mayoría de economías occidentales en las tres últimas décadas es el desempleo. Aunque en los últimos años la situación ha mejorado, el deficiente funcionamiento del mercado de trabajo sigue siendo uno de los rasgos más preocupantes de la economía española. Bentolila y Dolado (1991) sostienen que el aspecto geográfico del mercado de trabajo es importante a la hora de entender el elevado desempleo observado en España. La imperfecta articulación del mercado laboral español se refleja en las amplias y persistentes disparidades regionales en las tasas de desempleo. Este hecho es ilustrativo, en primer lugar, de la más que probable existencia de disparidades de equilibrio a largo plazo entre los correspondientes niveles regionales de las tasas de paro; y, en segundo lugar, es representativo de la falta de operatividad de los salarios para amortiguar las diferencias regionales en las tasas de desempleo. Así, este trabajo intenta explicar, desde una perspectiva macroeconómica, los amplios diferenciales en las tasas de paro entre Comunidades Autónomas y la persistencia de los mismos. La primera cuestión a responder es si existen diferencias regionales entre las tasas de desempleo de equilibrio y si, en caso de existir, se mantienen en el tiempo. Según Gómez y Usabiaga (2001), la acepción más empleada en la profesión para referirse al paro de equilibrio ha sido la de NAIRU (tasa de desempleo no aceleradora de la inflación). En este trabajo, al vincular desempleo y salarios regionales, nos centramos en la noción NAWRU (tasa de desempleo no aceleradora de los salarios) de forma que asociamos el equilibrio a la ausencia de aceleración de salarios. Así, hemos estimado las "time-varying" NAWRUs (método de Elmeskov) de las regiones españolas durante la década de los noventa. Por otro lado, un segundo elemento a dilucidar es si existen diferencias en el grado de rigidez salarial entre Comunidades Autónomas. Para aproximarnos al nexo de unión entre salarios y desempleo de las regiones españolas estimamos sus curvas de Phillips (ampliadas y reducidas). Por tanto, las dos preguntas centrales sobre las que pivota este trabajo aluden a: 1) La existencia de diferencias regionales entre las tasas de desempleo de equilibrio y su persistencia; 2) La existencia de diferencias en el grado de rigidez salarial entre Comunidades Autónomas. El interés de ambas cuestiones está vinculado a la explicación de las amplias disparidades en las tasas de paro regionales en España. Como sabemos, estos diferenciales son ineficientes pues, por ejemplo, introducen un sesgo inflacionista, al 1 Centro de Estudios Andaluces presionar los salarios más al alza las regiones con bajo paro, que lo que las que tienen alto desempleo lo hacen a la baja. El trabajo sigue la siguiente estructura: en la sección 2 comentamos los hechos estilizados del desempleo y los salarios regionales en España; en la sección 3 estimamos las tasas de paro de equilibrio de las comunidades autónomas españolas y exponemos la metodología seguida para calcularlas; en la sección 4, una vez calculado el desempleo cíclico utilizando como referencia las NAWRUs calculadas en la sección anterior, estimamos las curvas de Phillips regionales de la economía española; y, por último, en la sección 5, comentamos las principales conclusiones a las que llegamos y planteamos las posibles extensiones a nuestro análisis. 2. HECHOS ESTILIZADOS En este apartado realizamos varias representaciones sencillas de las series de datos objeto de nuestro estudio, que nos pueden proporcionar unas primeras intuiciones de cara al análisis econométrico posterior. 2.1. La evolución del desempleo regional Las variables esenciales de este trabajo son el desempleo y la tasa de inflación salarial. Respecto a la primera variable hemos utilizado datos trimestrales para la década de los noventa (1990.3-2000.4). En concreto hemos desestacionalizado1 los datos de la Encuesta de Población Activa. Por otro lado, la inflación salarial la hemos aproximado por la tasa de variación interanual de los salarios nominales (ganancia/hora trabajada), a partir de la Encuesta de Salarios de la Industria y los Servicios. En el gráfico 1 podemos observar la evolución en este período del desempleo en España. Mientras que en la primera parte del período el desempleo aumenta, en la última no para de descender. Así, se forma una de los dos típicas jorobas del paro en España (la otra se forma en el período premuestral, a mediados de los ochenta). Con escasas excepciones, éste es el perfil que se repite en el desempleo de las regiones españolas. En este punto debemos tener en cuenta que cuando comparamos la evolución de la tasa de paro de una determinada región con el resto del país, sus determinantes se derivan de dos fuentes distintas. Por una parte, tenemos que considerar los factores agregados nacionales que afectarían de forma similar a las distintas 2 Centro de Estudios Andaluces regiones. Estos elementos son consecuencia de la situación económica general del país, de las condiciones institucionales que afectan al mercado de trabajo en su conjunto (por ejemplo, reformas laborales de ámbito nacional), de los tipos de política económica que se instrumentan y, en general, de la situación económica internacional. Estos determinantes son los que están detrás del hecho estilizado anterior, pues provocan que las variables del mercado de trabajo, tanto a escala nacional como regional se muevan, en parte, de forma similar. Sin embargo, existe otro grupo de factores que pueden ser particulares de una determinada región, como, por ejemplo, el crecimiento diferencial de la población activa. Ahora bien, a pesar de ese perfil similar en la evolución del desempleo de las regiones españolas, se observan unas diferencias significativas en el nivel del paro regional (por ejemplo, en el segundo trimestre de 1994 la tasa de paro en Andalucía era del 34.9%, frente al 17.6% de Baleares -prácticamente el doble-). En el gráfico 1 hemos optado por representar, como ejemplos representativos, el perfil del desempleo en estos dos casos extremos. Dados estos diferenciales podemos plantear la hipótesis de que los mismos se deben a unas diferencias similares en las NAWRUs regionales de la economía española. Como este concepto no puede observarse directamente, podemos utilizar dos alternativas. En primer lugar, podemos estimar los parámetros que la determinan (esto es lo que hacemos en la sección tercera). La segunda alternativa consiste en observar la evolución conjunta de la inflación salarial y el desempleo, e inferir la posible evolución de dicha NAWRU. Ésa es la estrategia descriptiva que abordamos a continuación. 2.2. Las curvas de Phillips regionales Dado que nuestro trabajo empírico se centra en la estimación de curvas de Phillips regionales (una vez estimadas anteriormente las NAWRUs respectivas) nos parece obligado representar gráficamente lo que suele denotarse como las "curvas de Phillips” de las regiones españolas. Más concretamente, representamos la evolución conjunta (1990.1-2000.4) de los pares desempleo (abscisas)-inflación salarial (ordenadas). Si observamos la curva de Phillips en el conjunto de la economía española -gráfico 2- podemos observar tres etapas: a) Una primera etapa (aproximadamente hasta mediados de los años 90) en que la relación tiene el signo negativo esperado; b) una segunda etapa (hasta el año 1998) en que la relación es positiva (disminuye conjuntamente el desempleo y la inflación salarial), y c) una tercera etapa (que ocupa los 1 Para ello, hemos utilizado el Método Census X11 Multiplicativo. 3 Centro de Estudios Andaluces dos últimos años del período muestral) en que mientras el desempleo sigue reduciéndose de forma apreciable, la inflación salarial se estabiliza aproximadamente en torno al 2.3%2. TP PT Este patrón se repite (aunque de forma menos nítida), en líneas generales, en las curvas de Phillips de las regiones españolas. Antes de pasar al trabajo econométrico queremos destacar que lo anterior puede explicar que en en dicho trabajo obtengamos distintos signos (según las regiones) para el coeficiente que liga el desempleo cíclico y la inflación salarial (o que dicho coeficiente no resulte significativo). En última instancia, lo que estamos contrastando es si el mecanismo de determinación salarial al nivel de las regiones españolas es o no es competitivo. 3. LAS NAWRUS REGIONALES DE LA ECONOMÍA ESPAÑOLA: EL MÉTODO DE ELMESKOV La existencia de singularidades importantes en el comportamiento de las tasas de desempleo de las distintas Comunidades Autónomas, tanto en lo que concierne a sus niveles como a su evolución, apunta a la existencia de diferentes tasas de paro de equilibrio a nivel regional. Así pues, conocerlas es esencial para explicar la disparidad en las tasas de desempleo regional. En esta sección vamos a ofrecer estimaciones de las NAWRUs regionales siguiendo el método de Elmeskov. 3.1. El método de Elmeskov Existen múltiples métodos de estimación de la NAIRU. Dado que la tasa de paro de equilibrio no ha permanecido estable en el tiempo, lo adecuado es estimar una “time-varying” NAWRU. Una metodología bastante extendida es la desarrollada por Elmeskov (1993)3, donde se estima una NAWRU bajo el supuesto TP PT de que los cambios en la inflación salarial (salarios nominales) son proporcionales a la brecha del desempleo. Es decir: ∆2 wt = −α t (u t − u t* ); [1] 2 Podemos encontrar un microfundamento para este hecho estilizado en el modelo de Ball, Mankiw y Romer (1988) –sustituyendo la inflación salarial por la inflación per se-. En dicho modelo se predice que, a medida que en un país se reduce la inflación media (y, por tanto, disminuyen las expectativas de inflación y la curva de Phillips se desplaza hacia el origen), la relación inflación-desempleo se hace más plana. En este contexto, ante la forma plana que adopta la curva de Phillips en la última etapa, podríamos preguntarnos si también existe una Tasa Natural de Inflación. 3 Método ampliamente utilizado en el marco de la OCDE o el FMI –véase también Ball (1997)-. TP PT TP PT 4 Centro de Estudios Andaluces donde wt es el logaritmo neperiano de los salarios nominales, u t es la tasa de desempleo observada y u t* es la NAWRU4. Las dos variables inobservables de esa expresión, α t y ut* , se identifican bajo la restricción de TP PT que ambas deben permanecer constantes entre dos observaciones consecutivas. Una estimación de α t se obtiene para dos períodos consecutivos de la siguiente forma: ∆3 wt αt = − ; ∆u t [2] y sustituyendo esta última expresión en la anterior obtenemos la NAWRU ( ut* ): u t* = u t − ∆u t 2 ∆ wt ; ∆3 wt [3] Respecto a la NAWRU obtenida por este procedimiento hay que decir que se trata de un indicador de equilibrio a corto plazo, puesto que representa la tasa de desempleo asociada, en un período dado y vinculada a la evolución pasada reciente de las variables objeto de estudio, a un crecimiento salarial constante5. TP PT 3.2. Los resultados En el gráfico 3 se representa, a modo de ejemplo, la evolución de las NAWRUs alisadas en España, Andalucía y Baleares; por otra parte, en el cuadro 1 se recogen las estimaciones anuales de las NAWRUs de todas las regiones españolas. Cabe destacar dos grupos de regiones: 1) Regiones cercanas al "pleno empleo" (NAWRU en torno al “7-8%”), como Aragón, Baleares, Navarra y La Rioja; 2) Regiones de paro alto y persistente, como Andalucía y Extremadura. Además, hay que poner el acento en otro hecho, que se anticipa a los resultados del trabajo econométrico de la siguiente sección, y es que existe una apreciable histéresis (elevada correlación entre el desempleo observado y las NAWRUs estimadas). Por otro lado, se observa un perfil similar en la evolución de las distintas NAWRUs regionales, lo que está indicando que los diferenciales regionales de desempleo no se reducen en el período estudiado (hay diferenciales de equilibrio). 4 TP PT ∆ (filtro en diferencias) hace referencia a ∆k = (1 − L) k . 5 Debido a las características de la forma de obtención descrita, la NAWRU resultante es sumamente variable, de modo que lo habitual es alisar la serie original de la NAWRU estimada (mediante medias móviles, el filtro de HodrickPrescott, etc.). En nuestro caso, hemos alisado las NAWRUs regionales con el filtro de Hodrick-Prescott. TP PT 5 Centro de Estudios Andaluces 4. LA CURVA DE PHILLIPS DE LAS ECONOMÍAS REGIONALES ESPAÑOLAS La existencia de rigidez salarial supone la incapacidad que tienen los salarios de cambiar en sentido contrario que el desempleo. Por tanto, un supuesto relevante para explicar la magnitud, la persistencia y la disparidad de las tasas de desempleo regionales es el papel jugado por el comportamiento de los salarios y la relación que vincula a éstos con el desempleo6. El nexo de unión entre los salarios y el desempleo se puede TP PT sintetizar, siguiendo a Blanchard y Katz (1999), en dos mecanismos diferentes. El primero de estos mecanismos es consistente con la curva de Phillips, que, como sabemos, preconiza una relación inversa entre el ritmo de variación de los salarios y la tasa de desempleo. El segundo de los mecanismos es consistente con distintos modelos del mercado de trabajo y postula la existencia de una relación inversa entre los niveles de los salarios y las tasas de desempleo -lo que Blanchflower y Oswald (1994) han denominado como curva de salarios-. Con el fin de obtener una aproximación cuantitativa a la flexibilidad salarial de las regiones españolas, procederemos a estimar curvas de Phillips aumentadas para las distintas Comunidades Autónomas, aplicando una metodología común que nos permita comparaciones. 4.1. Curvas de Phillips de las regiones españolas Podemos considerar que la curva de Phillips es una representación de las pautas de ajuste dinámico de los salarios nominales a los cambios en un conjunto de factores que caracterizan el proceso macroeconómico de determinación de los salarios. Dado que solamente examinamos este proceso en la curva de Phillips, es importante especificar ésta de forma adecuada con el fin de obtener estimaciones de sus coeficientes que sean robustas. 4.1.1. Expresión general de la curva de Phillips En primer lugar, utilizaremos una expresión general de la curva de Phillips a corto plazo. En esta especificación la variable dependiente, la tasa de crecimiento interanual de los salarios nominales regionales por trabajador (∆W), se relaciona con la tasa de inflación interanual esperada (∆Pe), la tasa de paro (U), la P P variación interanual de la tasa de paro (∆U), para reflejar la noción de histéresis, con la tasa de crecimiento TP PT 6 Centro de Estudios Andaluces interanual de la productividad media del trabajo (∆PL) y con la tasa de crecimiento interanual retardada del precio del petróleo (∆Ppetr), que introducimos como aproximación de las perturbaciones de oferta. La expresión de la ecuación es la siguiente: ∆W it = κi + βi ∆ Pet + γ i Uit + φi ∆Uit + ϑi ∆PL t + ψi ∆Ppetr t −q + εit [4] Donde el subíndice i se refiere a una región individual y hay M observaciones de corte transversal; el subíndice t indica el periodo y hay T periodos de tiempo; el subíndice q indica el retardo introducido; y ε es el término de error. Ha sido habitual en la literatura empírica especificar la curva de Phillips incluyendo como argumento la desviación de la tasa de paro observada respecto a su valor de equilibrio. En muchos trabajos empíricos se ha considerado que la tasa de paro de equilibrio permanece estable a lo largo del periodo de estimación y que, por tanto, no es necesario incorporar esta variable ya que la constante estimada incorpora el impacto de la NAWRU. Probablemente, este supuesto es aceptable para el análisis de la economía norteamericana pero, sin embargo, es difícilmente defendible para una economía como la española. En nuestra especificación hemos reemplazado la tasa de paro por la tasa de desempleo cíclico, definida como la diferencia entre la tasa de paro observada y la NAWRU obtenida en la sección anterior. Este cambio supone introducir una variable endógena en la parte derecha de la ecuación ya que en el cálculo de la NAWRU se utiliza la tasa de variación de los salarios nominales, que es la variable dependiente de la curva de Phillips. Por tanto, la tasa de paro cíclico está correlacionada con el término de error, por lo que la estimación por mínimos cuadrados ordinarios está sesgada y es inconsistente. La solución estándar en casos como éste es estimar la ecuación utilizando el método de variables instrumentales. El instrumento utilizado para el paro cíclico es dicha variable retardada 4 periodos. Este instrumento está correlacionado con la variable explicativa endógena y no está correlacionado con las perturbaciones. TP 6 Castillo et al. (1998) encuentran evidencia de que, a pesar de que España y Portugal han experimentado perturbaciones similares, la tasa de desempleo en España ha sido mucho mayor debido a que los salarios han sido más rígidos en este país. PT 7 Centro de Estudios Andaluces 4.1.2 Expresión reducida de la curva de Phillips En sus estudios a nivel regional, Hyclak y Johnes (1989), Payne (1995) y Baddeley et al. (2002) utilizan una expresión más simple de la curva de Phillips. En esta especificación, la variable dependiente, la tasa de crecimiento interanual de los salarios nominales regionales por trabajador (∆W), únicamente depende de la tasa de inflación interanual esperada (∆Pe) y de la tasa de paro anual (U), siendo la expresión de la P P curva de Phillips la siguiente: ∆W it = κi + βi ∆ Pet + γ i Uit + µit [5] Donde el subíndice i se refiera a una región individual y hay M observaciones de corte transversal; el subíndice t indica el periodo y hay T periodos de tiempo; y µ es el término de error. Al igual que con la expresión general (4), hemos sustituido la tasa de desempleo por la tasa de paro cíclico, definida como la desviación de la tasa de paro observada respecto a su valor de equilibrio. 4.1.3. Definición de las variables, fuentes de datos y métodos de estimación Los datos utilizados para estimar las curvas de Phillips de las regiones españolas proceden de la Encuesta de Salarios de la Industria y los Servicios, del Índice de Precios de Consumo (IPC), de la Encuesta de Población Activa (EPA) y la Contabilidad Nacional de España (CNE), elaborados todos ellos por el Instituto Nacional de Estadística. El periodo analizado comprende los años entre 1989 y 2000, ambos inclusive, y la periodicidad de los datos es trimestral. La tasa interanual de crecimiento de los salarios nominales (∆W) la aproximamos por la diferencia logarítmica de la ganancia por hora trabajada7 en la industria y los servicios8; la inflación esperada (∆Pe) la TP PT TP PT P P hemos medido a través de la variación interanual del logaritmo del Índice de Precios al Consumo (IPC) nacional: ∆ P te = log( IPCt − q ) − log( IPC t − 2q ) = ∆Pt − q [6] donde, como justificaremos a continuación, utilizamos la hipótesis de expectativas adaptativas; la tasa de desempleo (U) es la tasa de paro trimestral desestacionalizada expresada en tanto por uno; la tasa de desempleo cíclica (Uc) se define como la diferencia entre la tasa de paro trimestral desestacionalizada y la 7 Los datos agregan los pagos totales por ambas jornadas, ordinaria y extraordinaria, de todo tipo de contrato, de todas las secciones y de todas las categorías. TP PT 8 Centro de Estudios Andaluces tasa de paro de equilibrio (NAWRU), obtenida para cada región y periodo en la sección anterior; la variación interanual de la tasa de desempleo (∆U) lo hemos calculado como la diferencia interanual de la tasa de paro trimestral; el crecimiento interanual de la productividad media del trabajo (∆PL) viene dado por la variación logarítmica de la ratio del PIB nacional a precios constantes, datos ciclo-tendencia, y los ocupados, medidos por el número de puestos de trabajo equivalentes a tiempo completo, datos ciclo-tendencia; y la tasa de variación interanual del precio en dólares norteamericanos del barril de petróleo North Sea Brent9 (∆Ppetr), TP PT con cuatro retardos. Una cuestión crucial, relacionada con la definición de las variables, es cómo especificar adecuadamente las expectativas de inflación, pues esta es una variable no observable. En el análisis se asumen expectativas adaptativas ya que una especificación con expectativas formuladas “mirando hacia atrás” (backward-looking) parece estar más de acuerdo con la existencia de indexación, lo que significa que los cambios en los salarios nominales reflejan esencialmente un ajuste ex-post a las variaciones en los precios, lo que sugiere que la inflación pasada, en lugar de la inflación esperada, es el concepto más relevante en la determinación de los salarios. En la especificación backward-looking, el número de retardos sobre la inflación pasada refleja la velocidad de la indexación y la duración normal de los contratos. Dado que España se caracteriza por un ciclo de negociación anual, y los datos son de periodicidad trimestral, utilizamos la tasa de inflación con cuatro retardos como proxy de las expectativas de inflación (q=4)10. TP PT Por otro lado, los errores en las ecuaciones de salarios incluyen, sin lugar a dudas, factores que son comunes a todas las regiones, tales como la política macroeconómica nacional, la legislación laboral o convenios colectivos sectoriales con efectos espaciales amplios, así como otros factores que son específicos de cada región. Estimar las ecuaciones por separado desaprovecha esta información. Por ello, parece recomendable estimar las ecuaciones conjuntamente, en vez de ignorar estas conexiones. Dado que disponemos de los datos estructurados en forma de panel, hemos estimado un sistema de ecuaciones. 8 Al excluir las remuneraciones del sector público, evitamos provocar una infravaloración de la semielasticidad del salario nominal respecto al desempleo por la menor influencia de éste en los funcionarios. 9 Los datos proceden de The Economist y Financial Times. 10 En los últimos años, dentro de la línea New Keynesian, se ha desarrollado lo que ha venido en denominarse la nueva curva de Phillips y donde se pone el énfasis en el componente forward-looking de las expectativas de inflación. Sin embargo, en estos trabajo (a diferencia del nuestro) la variable endógena es la propia inflación de precios y no la de salarios. Además, Galí y López-Salido (2001) resaltan la importancia del componente backward-looking en la inflación de la economía española. PT TP PT TP TP PT 9 Centro de Estudios Andaluces 4.2. Medidas de la rigidez salarial Los coeficientes estimados de la inflación (β) y del desempleo cíclico (γ) nos permiten construir medidas del grado de flexibilidad salarial. El parámetro β es la elasticidad de los salarios nominales con respecto a la inflación y nos da una idea del nivel de indexación salarial de la economía. El coeficiente γ es la semi-elasticidad [Klau y Mittelstadt (1986)] de los salarios nominales con respecto a la tasa de desempleo cíclico. A partir de ellos, Coe (1985), Hyclak y Johnes (1989), Payne (1995) y McMorrow (1996) definen un sencillo indicador del grado de rigidez a corto plazo de los salarios reales como la ratio entre el coeficiente β y el valor absoluto del coeficiente γ. Por su parte, la inversa del valor absoluto del coeficiente γ es definido como el índice a largo plazo de la rigidez de los salarios reales y hace referencia a la reacción de los salarios reales ante cambios en la presión de la demanda, aproximada por el paro cíclico. Si el proceso de determinación de salarios se caracteriza por un ajuste lento de los salarios nominales ante cambios en los precios, entonces los salarios reales serán más flexibles ante una perturbación que tenga efectos inflacionistas. Por tanto, la rigidez de los salarios reales será mayor cuanto más rápidamente respondan los salarios nominales a un cambio en los precios. La sensibilidad de los salarios nominales al desempleo cíclico determina la capacidad de la economía para adaptarse a una perturbación que altere el nivel de actividad económica a través de movimientos salariales. Consecuentemente, cuanto menos elásticos sean los salarios respecto al desempleo cíclico mayor será la rigidez de los salarios reales y, por tanto, más difícil y lento el ajuste de la economía. 4.3. Los resultados Los resultados de la estimación de la expresión general de las curvas de Phillips (ecuación [4]) para las regiones españolas (véase cuadro 2) definen cinco grupos: a) Regiones (Aragón, Extremadura, Madrid, Navarra, País Vasco y La Rioja) caracterizadas por una clara indexación de los salarios, donde ninguna otra variable explicativa resulta significativa; b) Regiones (como Andalucía) donde se detecta un alto grado de histéresis, pues es significativa la variación de la tasa de paro, pero no el nivel del desempleo cíclico; c) Regiones (Asturias, Canarias, Cataluña, Castilla y León y Castilla-La Mancha) donde las variables tasa de paro cíclico y variación de la tasa de paro son significativas pero tienen signos opuestos; d) Regiones (Baleares y Cantabria) donde la tasa de paro cíclico o la variación de la tasa de paro son significativos pero 10 Centro de Estudios Andaluces con signo positivo; e) Regiones (Valencia, Galicia y Murcia) donde la curva de Phillips tiene escaso poder explicativo del crecimiento de los salarios nominales. En algunas regiones, los regresores tasa de paro cíclico, variación de la tasa de desempleo y crecimiento de la productividad están altamente correlacionados. Este factor provoca que en alguna de las estimaciones realizadas hayamos detectado problemas de multicolinealidad, por lo que no es posible analizar con precisión los efectos individuales de cada uno de los regresores. Los coeficientes obtenidos tienen un signo opuesto al esperado o una magnitud poco creíble. Sin embargo, como hemos comentado anteriormente, algunos trabajos empíricos apoyan una especificación simplificada de la curva de Phillips (ecuación [5]) que, al no incluir las variaciones de la tasa de paro y de la productividad como variables explicativas, sortea el problema de multicolinealidad al que nos enfrentamos. Sin embargo, los resultados obtenidos (véase cuadro 3) no difieren demasiado de los que se han derivado de una curva de Phillips más ampliada. La falta de significatividad de la tasa de paro cíclico en muchas regiones o que esta variable aparezca con signo opuesto al que postula la teoría es un puzzle que puede estar causado, entre otros factores, por el periodo muestral analizado. Podemos interpretar estos resultados argumentando que el citado coeficiente resulta ser no significativo porque la mayoría de las regiones españolas se caracterizan por una elevada rigidez salarial y, por tanto, la tasa de paro cíclico tiene escaso poder explicativo en el modelo o que tiene un signo cambiado al esperado porque en el periodo analizado, particularmente entre 1994 y 1999, se produce un descenso continuado y conjunto de la tasa de desempleo y de la tasa de inflación. Hay dos posibles explicaciones sobre el citado comportamiento de la inflación y el desempleo: Se podría argumentar, siendo excesivamente optimistas, que las reformas del mercado de trabajo de 1994 y 1997 han cambiado sustancialmente la legislación sobre el despido, los mecanismos de fijación de salarios y el sistema de bienestar en España, y que estos factores están detrás del descenso conjunto en la tasa de paro y en la inflación. Ello supondría un cambio permanente en la forma en que la inflación reacciona al desempleo. Alternativamente, Blanchard y Jimeno (1999) sostienen que las reformas supusieron cambios moderados en el mercado de trabajo y ponen el énfasis en dos hechos puntuales que supusieron sendos desplazamientos de la curva de Phillips. Primero, para evitar la reducción de la protección del empleo, amenazada por la reforma de 1994, los sindicatos negociaron menores incrementos salariales a cambio de no aplicar la reducción en los costes de despido. El resultado fue una reducción transitoria de la inflación salarial. Segundo, aproximadamente al mismo tiempo, 11 Centro de Estudios Andaluces se produjo una mayor credibilidad en la política antiinflacionista por el cambio en el régimen de política monetaria (autonomía del Banco de España y una estrategia de objetivos directos de inflación) y por un aumento de la probabilidad de que España entrase en la UME, que provocaron un descenso de las expectativas de inflación, dando lugar a un desplazamiento favorable de la curva de Phillips. 5. CONCLUSIONES El objetivo del trabajo ha sido buscar el origen de las amplias y persistentes disparidades regionales en las tasas de desempleo de las comunidades autónomas españolas, centrándonos en dos hechos: en primer lugar, la existencia de distintas tasas de paro de equilibrio; y, en segundo lugar, el diferente grado de rigidez salarial. La comparación de las NAWRUs regionales, estimadas mediante el método de Elmeskov, pone de relieve dos hechos: 1) En primer lugar, la existencia de importantes diferencias de equilibrio entre las Comunidades Autónomas, fenómeno que explica la disparidad de las tasas de paro regionales; 2) En segundo lugar, la simetría en su evolución, explicaría la persistencia de tales diferencias. El análisis del grado de rigidez salarial lo hemos tratado de medir a través de curvas de Phillips regionales. Sin embargo, el periodo muestral se caracteriza, entre 1994 y 1999, por la reducción simultánea de la tasa de inflación y la tasa de paro, lo que contradice la teoría (una curva de Phillips a corto plazo con pendiente negativa). A pesar de ello, como predice la teoría, algunas de las regiones con mayor tasa de paro muestran menor grado de respuesta de los salarios ante el desempleo. Como posibles extensiones del análisis desarrollado en este trabajo podemos apuntar las tres siguientes: a) Dada la importancia del objetivo de "pleno empleo" sería interesante constrastar la existencia (o, en su caso, la lejanía) de pleno empleo al nivel de las regiones españolas; b) Otra extensión natural de nuestro trabajo sería diseccionar los determinantes del desempleo de equilibrio de cada una de las regiones españolas; y c) Podría resultar enriquecedor ampliar el análisis para considerar la posibilidad de la existencia de asimetrías y no linealidades en las curvas de Phillips regionales españolas. 12 Centro de Estudios Andaluces Referencias bibliográficas - - - - Baddeley, M.; Martín, R. y Tyler, P. (2002), “Regional Wage Rigidity: The European Union and United States Compared”, Journal of Regional Science, 40(1), págs. 115-142. Ball, L., Mankiw, N. G. y Romer (1988): "The New Keynesian Economics and the Output-Inflation Trade-Off", Brookings Papers on Economic Activity, 1, págs. 1-65. Ball, L. (1997): “Disinflation and the NAIRU”, en Romer C.D. y Romer, D.H. (Eds.) (1997): Reducing Inflation: Motivation and Strategy, University of Chicago Press, Chicago, págs. 167-192. Bentolila, S. y Dolado, J. (1991), “Mismatch and Internal Migration in Spain, 1962-86”, en PadoaSchioppa, F. (ed), Mismatch and Labour Mobility, Cambridge University Press, Cambrige, págs. 182234 Blanchard, O. y Katz, L. (1999), “Wage Dynamics: Reconciling Theory and Evidence”, American Economic Review. Papers and Proceedings, may, págs. 69-74. Blanchard, O. y Jimeno, J. F. (1999), “Reducing Spanish Unemployment under the EMU”, Documento de Trabajo de FEDEA, 99-02. Blanchflower, D. y Oswald, A. (1995), “An Introduction to the Wage Curve”, Journal of Economic Perspectives, 9, págs. 153-167. Castillo, Dolado y Jimeno (1998), “A tale of Two Neighbour Economies: Does Wage Flexibility Make the Difference between Portuguese and Spanish Unemployment?” Documento de Trabajo de FEDEA, 98-02. Coe, D. T. (1985), “Nominal Wages, the NAIRU and Wage Flexibility”, OECD Economic Studies, 5, págs. 87-126. Elmeskov, J. (1993): "High and Persistent Unemployment: Assessment of the Problem and Its Causes", OECD Economics Department, Working Paper nº 132. Galí, J. y López-Salido, D. (2001), “Una Nueva Curva de Phillips para España”, Moneda y Crédito, 212, págs. 265-304. Gómez, F. y Usabiaga, C. (2001): “Las Estimaciones del Desempleo de Equilibrio. Una Panorámica”, Revista de Economía Aplicada, 9(27), págs. 103-129. Hyclak, T. y Johnes, G. (1989), “Real Wage Rigidity in Regional Labor Markets in the U.K., the U.S., and West Germany”, Journal of Regional Science, 29(3), págs. 423-432. Klau, F. y Mittelstadt, A. (1986), “Labour Market Flexibility”, OECD Economic Studies, 6, págs. 7-45. McMorrow (1996) “The Wage Formation Process and Labour Market Flexibility in the Community, The US and Japan”, Economic Papers, 118. Payne, J. E. (1995), “A Note on Real Wage Rigidity and State Unemployment Rates”, Journal of Regional Science, 35(2), págs. 319-332. 13 35% 30% 25% 20% 15% 10% 5% 0% 1 9 9 0 ;3 1 9 9 1 ;3 1 9 9 2 ;3 1 9 9 3 ;3 1 9 9 4 ;3 1 9 9 5 ;3 1 9 9 6 ;3 1 9 9 7 ;3 1 9 9 8 ;3 1 9 9 9 ;3 2 0 0 0 ;3 Tasa Desempleo_Esp Tasa Desempleo_And Tasa Desempleo_Bal Gráfico 2: Curva de Phillips en España (1990.1 - 2000.4) 10% 9% Tasa Inflación Salarial Centro de Estudios Andaluces 40% Gráfico 1: Tasa de Desem pleo en España, Andalucía y Baleares (1990.3 - 2000.4) 8% 7% 6% 5% 4% 3% 2% 1% 0% 10% 12% 14% 16% 18% 20% 22% Tasa Desem pleo (desestacionalizada) 24% 26% 14 Centro de Estudios Andaluces Gráfico 3: NAWRUs en España, Andalucía y Baleares (1990.3 - 2000.4) 40% 35% 30% 25% 20% 15% 10% 5% 0% 19 90 ;3 19 91 ;1 19 91 ;3 19 92 ;1 19 92 ;3 19 93 ;1 19 93 ;3 19 94 ;1 19 94 ;3 NAWRUHP_BAL 19 95 ;1 19 95 ;3 19 96 ;1 19 96 ;3 NAWRUHP_AND 19 97 ;1 19 97 ;3 19 98 ;1 19 98 ;3 19 99 ;1 19 99 ;3 20 00 ;1 20 00 ;3 NAWRUHP_ESP CUADRO 1. NAWRUS ANUALES ESTIMADAS PARA LAS REGIONES ESPAÑOLAS (1990-2000). MÉTODO DE ELMESKOV (SUAVIZADAS CON HP) España Andalucía Aragón Asturias Baleares Canarias Cantabria Cataluña Castilla y León Castilla-La Mancha Extremadura Galicia C. Madrid Murcia Navarra País Vasco La Rioja C. Valenciana 1990 16,9 26,17 8,5 17,06 10,33 23,87 15,93 13,17 15,35 12,38 24 11,76 11,18 16,64 11,54 18,49 8,74 14,55 1991 17,67 27,76 10,05 17,83 11,14 24,56 17,1 14,17 16,6 13,51 24,87 12,9 13,05 18,59 11,94 19,57 10,23 16,3 1992 18,89 29,81 12,04 18,93 12,22 25,37 18,66 15,7 18,23 15,07 26,08 14,44 15,53 21,1 12,51 21,01 12,19 18,58 1993 20,33 31,59 13,78 20,08 13,25 25,81 20,18 13,37 19,64 16,66 27,34 15,92 17,77 23,2 13,03 21,3 13,96 20,62 1994 21,71 32,83 14,98 20,95 13,97 25,63 21,46 18,73 20,56 17,98 28,53 17,09 19,31 24,54 13,29 23,1 15,22 22,02 1995 22,6 33,36 15,43 21,31 14,15 24,63 22,18 19,25 20,79 18,76 29,33 17,73 19,87 24,78 13,14 23,18 15,68 22,41 1996 22,81 33,06 15,07 21,22 13,68 22,92 22,11 18,8 20,34 18,95 29,46 17,9 19,45 23,81 12,54 22,51 15,22 21,75 1997 22,3 32,01 13,94 20,76 12,64 20,73 21,1 17,48 19,27 18,53 28,92 17,74 18,19 21,79 11,6 21,09 13,99 20,19 1998 21,07 30,38 12,2 19,99 11,17 18,35 19,22 15,49 17,67 17,53 27,88 17,3 16,32 19,05 10,55 18,93 12,36 17,97 1999 19,24 28,36 10,2 19 9,43 16,02 16,86 13,09 15,67 16,06 26,6 16,64 14,12 15,87 9,52 16,12 10,56 15,47 2000 17,15 26,11 8,17 17,91 7,56 13,76 14,36 10,58 13,41 14,34 25,23 15,91 11,83 12,52 8,54 12,88 8,67 12,93 15 Centro de Estudios Andaluces CUADRO 2. CURVAS DE PHILLIPS – EXPRESIÓN GENERAL SISTEMA DE ECUACIONES Variable dependiente: tasa de crecimiento interanual de los salarios nominales (∆W) Método de estimación: variables instrumentales Periodo muestral: 1991:3 -2000:4 Número de regiones: 17 Número de observaciones: 39 CCAA Andalucía Aragón Asturias Baleares Canarias Cantabria Castilla y León Castilla-La Mancha Cataluña Com. Valenciana Extremadura Galicia Madrid Murcia Navarra País Vasco La Rioja Cte. (κ) ∆P (β) Uc (γ) ∆U (φ) ∆PL ( ϑ ) ∆Ppetr (ψ) -0,042626 (-3,984029) 0,006395 (0,769779) 0,001831 (0,181920) -0,004811 (-0,621947) 0,016759 (1,395353) -0,017739 (-2,665880) -0,019399 (-1,078276) -0,012157 (-1,207660) 0,013037 (2,433844) 0,048404 (1,474532) 0,000160 (0,015347) 0,025176 (2,873396) 0,014235 (1,203148) 0,034021 (2,304760) 0,003202 (0,478825) 0,014067 (2,147523) -0,011151 (-1,559154) 1,968066 (7,181236) 0,839845 (3,903204) 0,863224 (2,872745) 1,221902 (5,668915) 0,981880 (3,042286) 2,026188 (11,52244) 1,453835 (3,513389) 1,385013 (5,183674) 0,904964 (6,468718) -0,875468 (-1,962775) 0,968956 (3,534140) 0,496423 (2,049793) 0,701939 (2,366541) 0,113884 (0,284476) 1,152188 (6,550717) 0,694307 (4,169910) 1,597004 (8,564717) -0,086815 (-0,387426) 0,138069 (0,699103) -1,133234 (-3,820472) 0,454067 (3,027098) -1,838437 (-4,067916) 0,155742 (1,215028) 1,339559 (2,849706) 0,555944 (2,212333) -0,280596 (-2,658953) -0,216675 (-0,761147) -0,034793 (-0,149591) 0,620015 (2,070403) -0,323934 (-1,291330) 0,098222 (0,193830) 0,282658 (1,382006) 0,011768 (0,061594) -0,088556 (-0,367179) -0,580475 (-3,478143) 0,146831 (1,142750) 0,437192 (2,134797) -0,057321 (-0,583735) 1,072175 (4,124000) 0,271272 (3,156002) -0,645158 (-2,057437) -0,412999 (-2,055395) 0,211164 (2,717048) 0,238572 (1,095470) -0,227355 (-1,190571) 0,086356 (0,476755) -0,029362 (-0,178424) 0,120854 (0,408078) -0,258540 (-1,780208) 0,167715 (1,278978) -0,121243 (-0,876234) 0,670994 (1,839126) 0,033506 (0,105641) 0,191253 (0,455365) 0,061067 (0,177718) 0,308799 (0,625842) -1,464921 (-5,282327) -0,008038 (-0,024529) 0,640622 (1,870326) -0,179417 (-0,859979) 0,663705 (1,874601) 0,586695 (1,434171) -0,399602 (-1,033582) -0,001354 (-0,004857) 0,938440 (1,732237) 0,491568 (1,983758) 0,255608 (1,017676) 0,381768 (1,278257) -0,023356 (-2,236203) -0,017476 (-1,979815) 0,008654 (0,707106) -0,015749 (-1,622021) 0,010929 (0,785203) -0,017123 (-2,200510) -0,001292 (-0,141177) -0,010828 (-1,062463) 0,003709 (0,640547) 0,012980 (1,383715) 0,016835 (1,394263) -0,008568 (-0,780263) 0,009481 (1,228673) 0,028230 (1,853217) -0,003667 (-0,471469) -0,002863 (-0,424864) 0,000112 (0,013379) AR(1) R2 ajust. P P 0,585358 0,481377 0,529638 0,650174 0,561709 0,785984 0,607931 (9,822409) 0,587079 0,627335 0,694367 0,911092 (14,84252) 0,762400 0,321659 0,260885 0,553681 (5,675682) 0,693965 0,216175 0,699993 0,592794 0,737072 NOTA: Los t-ratios aparecen entre paréntesis. Se ha contrastado la existencia de autocorrelación mediante el test de Breusch y Godfrey y en caso de detectar la existencia de autocorrelación se han modelizado las perturbaciones mediante un esquema autorregresivo de primer orden. 16 Centro de Estudios Andaluces CUADRO 3. CURVAS DE PHILLIPS – EXPRESIÓN REDUCIDA SISTEMA DE ECUACIONES Variable dependiente: tasa de crecimiento interanual de los salarios nominales (∆W) Método de estimación: variables instrumentales Periodo muestral: 1991:3 – 2000:4 Número de regiones: 17 Número de observaciones: 39 CCAA Andalucía Aragón Asturias Baleares Canarias Cantabria Castilla y León Castilla-La Mancha Cataluña Com. Valenciana Extremadura Galicia Madrid Murcia Navarra País Vasco La Rioja Cte. (κ) ∆P (β) Uc (γ) AR(1) R2 ajust. -0,014725 (-1,271602) 0,004832 (0,641559) -0,010382 (-1,161113) -0,001144 (-0,151646) -0,011354 (-0,628695) -0,023709 (-3,225993) 0,012170 (0,945795) 0,005635 (0,646553) 0,005097 (1,043363) 0,041927 (1,670596) 0,005111 (0,579727) 0,023095 (2,919224) 0,019774 (1,791770) 0,029595 (2,218644) 0,007521 (1,226756) 0,011438 (1,994194) -0,011312 (-1,617868) 1,487186 (5,577787) 0,854723 (4,638670) 1,311613 (6,296676) 1,158521 (6,451596) 1,586311 (3,733489) 1,685354 (9,894332) 0,743681 (2,464110) 1,146299 (5,287541) 1,045514 (9,364530) -0,263307 (-0,706629) 1,041458 (4,887734) 0,453496 (2,316686) 0,560781 (2,149067) 0,540762 (1,794996) 1,213762 (8,946305) 0,871640 (7,104683) 1,711686 (10,72060) -0,233043 (-1,009866) 0,375377 (2,720501) -0,616707 (-3,458235) 0,447587 (4,317862) -0,253233 (-0,928575) 0,069659 (0,586006) 0,115787 (0,268189) 0,610604 (3,076009) -0,127926 (-1,549765) 0,220420 (1,043468) -0,099477 (-0,613561) 0,493983 (2,890399) -0,249192 (-1,314496) 0,354657 (1,345451) 0,125089 (1,028498) 0,233901 (2,013406) -0,243789 (-1,831979) 0,324676 (3,117162) 0,615357 P P 0,459587 0,520976 0,656276 0,409254 (4,300748) 0,502628 0,710839 0,568302 (7,446895) 0,586314 0,615375 0,673993 0,883632 (14,62433) 0,736298 0,349033 0,295389 0,687177 (7,935353) 0,713696 0,181259 0,696885 0,618505 0,757406 NOTA: Los t-ratios aparecen entre paréntesis. Se ha contrastado la existencia de autocorrelación mediante el test de Breusch y Godfrey y en caso de detectar la existencia de autocorrelación se han modelizado las perturbaciones mediante un esquema autorregresivo de primer orden. 17