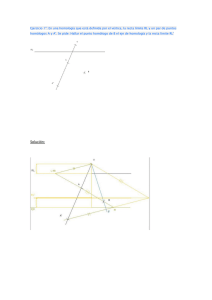
El eje, la recta límite y un punto homólogo cualquiera de la figura
Anuncio

El eje, la recta límite y un punto homólogo cualquiera de la figura dada. (Ilustración 6) Este ejercicio se resuelve de la misma forma que el anterior, sólo hay que determinar el centro de homología. RL A B C EJE Para hallar el centro de homología se aplica el siguiente método: B' 1º) Trazar una recta que una al punto transformado (B) con su homólogo (B’). 2º) Prolongar un lado que contenga al homólogo del transformado (B’). En la ilustración nº 6 se ha prolongado el lado BC hasta que corte a la recta límite en un punto (N) y al eje en otro punto. 3º) Unir el punto anterior mediante una recta con el transformado dado (B’) y por el otro punto (N) trazar una paralela al segmento anterior que pasa por B’ hasta que corte a la recta BB’ en un punto (O) este será el centro de homología. 4º) Para completar la figura se trazan rectas desde O y que pasen por los otros vértices del triángulo A y C. La recta que pasa por O y C cortará al segmento paralelo a ON y que pase por B’ en un punto C’ homólogo de C. O RL N M A B C EJE C' B' A' ILUSTRACIÓN Nº 6 Dirección EJE Para completar la figura transformada se puede aplicar el paso 5 del caso anterior. A B C Las dos rectas límites y el centro de homología. B' A' O A Una vez hallado el eje de simetría y conocidos todos los elementos se aplica cualquiera de los métodos explicados anteriormente (Ilustración 8) C' B' A' ILUSTRACIÓN Nº 7 d O RL A R' L' B Para determinar el centro y el eje de homología es necesario recordar la definición de homología: “Dos puntos homólogos (A y A’) están alineados con un punto fijo (O) llamado centro de homología, y: “dos rectas homólogas se cortan en una recta llamada eje de homología”. Aplicando lo anterior uniendo los puntos A y B con sus homólogos A’ y B’ mediante rectas, éstas se cortarán determinando el centro de homología O. Para determinar el eje de homología se prolongan las rectas homólogas AB y A’B’ hasta que se corten en un punto (P) que pertenecerá a dicho eje, sólo queda trazar por dicho punto (P) una paralela a la dirección dada. Una vez determinados todos los elementos se aplica cualquiera de los métodos explicados anteriormente. P C d Dos puntos homólogos de la figura dada y la dirección del eje. EJE O C' RL N M d En la ilustración nº 7 se observa que los lados del triángulo transformado (A’B’C’) son paralelos a las rectas determinadas por su recta límite y el centro de homología (OM y ON). Así mismo los lados del triángulo homólogo (ABC) son paralelos a las rectas determinadas por su recta límite y el centro de homología (OP). B C A R' L' EJE B P C d Para determinar el eje de homología se aplica lo explicado en el apartado de rectas límites: la distancia entre una recta límite y el centro de homología es igual a la distancia que existe entre la otra recta límite y el eje (Ilustración nº 3). C' B' A' ILUSTRACIÓN Nº 8