Respuesta de Frecuencia Diagramas de Bode
Anuncio
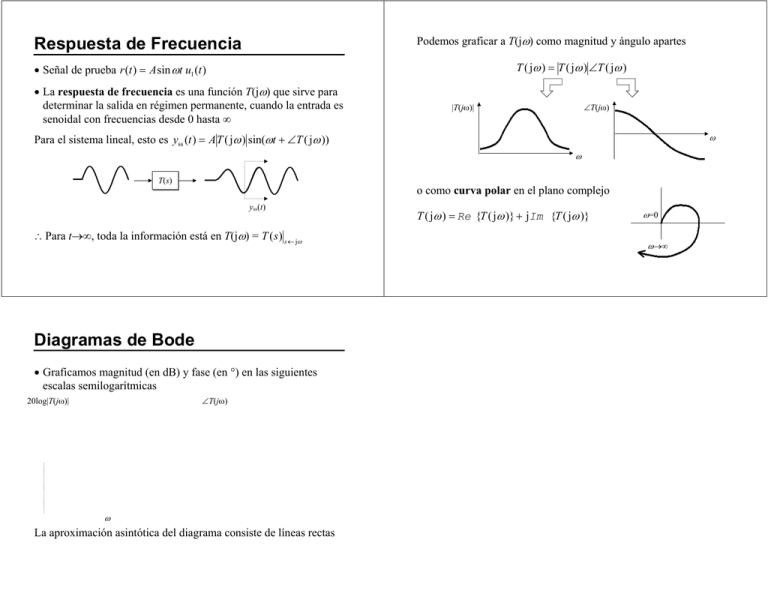
Podemos graficar a T(jw) como magnitud y ángulo apartes
Respuesta de Frecuencia
T ( jw ) = T ( jw ) ÐT ( jw )
· Señal de prueba r (t ) = A sin wt u1 (t )
· La respuesta de frecuencia es una función T(jw) que sirve para
determinar la salida en régimen permanente, cuando la entrada es
senoidal con frecuencias desde 0 hasta ¥
ÐT(jw)
|T(jw)|
Para el sistema lineal, esto es yss (t ) = A T ( jw ) sin(wt + ÐT ( jw ))
w
w
T(s)
o como curva polar en el plano complejo
yss(t)
\ Para t®¥, toda la información está en T(jw) = T ( s ) s ¬ jw
Diagramas de Bode
· Graficamos magnitud (en dB) y fase (en °) en las siguientes
escalas semilogarítmicas
ÐT(jw)
20log|T(jw)|
w
La aproximación asintótica del diagrama consiste de líneas rectas
T ( jw ) = Re {T ( jw )} + jIm {T ( jw )}
w=0
w®¥
Polo
1
s
+1
w1
0
0°
–20
–45°
–90°
w1
10w1
180°
0
90°
0°
w1
æ s
ö
çç + 1÷÷
è w1 ø
10w1
æ s ö 2z
çç ÷÷ +
s +1
è wn ø wn
–90°
–20
10
¥
0
0°
–40
–180°
wn
10wn
· Para z < 0.707, la frecuencia resonante está en
w r = w n 1 - 2z 2
y la ganancia máxima es
1
M máx = T ( jw r ) =
2z 1 - z 2
wn
10w1
–90°
2
–40
–180°
w1
10w1
0.1w1 w1
10w1
0°
0
–90°
2
0
0.1w1 w1
0°
0
Polos complejos
1
2
æ s ö
çç ÷÷ + 1
è wn ø
40
10w1
Polo doble
1
10
1
Caso especial: polos
en eje imaginario
1
w1
0
1
Polo en origen
1
s
0.1w1
90°
20
Cero en origen
s
Cero doble
2
æ s
ö
çç + 1÷÷
è w1 ø
–40
–180°
wn
10wn
0.1wn
wn
10wn