1. Aproximación de Controladores Continuos
Anuncio

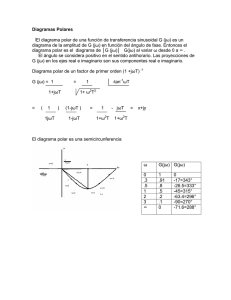
1. Aproximación de Controladores Continuos 1. Aproximación de Controladores Continuos ____________________________ 1 1.1. Introducción ________________________________________________________ 2 1.2. Aproximación Basada en la Función de Transferencia _____________________ 2 1.1.1. Aproximación de Tustin ______________________________________________ 2 1.1.2. Problemas en el dominio Frecuencia _____________________________________ 3 1.1.3. Respuestas Equivalentes ______________________________________________ 5 1.3. Aproximación Basada en Variables de Estado ____________________________ 8 1.4. Métodos Basados en Respuesta en Frecuencia ___________________________ 10 1.1.4. Método de la Transformada w _________________________________________ 10 Control Digital 08.doc 1 1.1. Introducción Muchas veces ya existe un controlador analógico Se intenta reproducir su comportamiento Con un período de muestreo pequeño se puede solucionar. 1.2. Aproximación Basada en la Función de Transferencia Se intenta aproximar G ( s ) u(t) u(kt) CAD y(kt) Algoritmo y(t) CDA text Reloj 1.1.1. Aproximación de Tustin aproximación de derivada como una diferencia en adelanto (método de Euler) px = dx ( t ) dt ≈ x (t + T ) − x ( t ) T = q −1 x (t ) T [1.1] como una diferencia hacia atrás px = dx ( t ) dt ≈ x (t ) − x (t − T ) T = q −1 x (t ) qT [1.2] en transformadas significa reemplazar s= z −1 z −1 o s= T zT [1.3] que corresponden a un desarrollo en serie truncado Para el método de Euler z = esT ≈ 1 + sT [1.4] para la diferencia hacia atrás z = esT ≈ 1 1 − sT [1.5] Otra aproximación: el método trapezoidal o método de Tustin Control Digital 08.doc 2 z = esT sT 2 ≈ sT 1− 2 1+ [1.6] Se reemplaza directamente s por alguna de sus aproximaciones: Euler s′ = z −1 T [1.7] diferencia hacia atrás s′ = z −1 zT [1.8] Tustin o bilineal s′ = 2 z −1 T z +1 [1.9] de este modo se obtiene H ( z ) = G ( s′ ) [1.10] La figura muestra el mapeo del semiplano negativo de s Plano Z Diferencia en Adelanto Diferencia en Atraso Tustin 1.1.2. Problemas en el dominio Frecuencia Con estas aproximaciones se distorsiona la escala de frecuencias. Si se quiere digitalizar un filtro pasa banda o notch puede haber distorsiones. Ejemplo: transmisión de una senoide a través de un filtro con BO0 Control Digital 08.doc 3 H ( e jωT ) = 2 e jωT −1 1 jωT 1 − e G ( ) T e jωT + 1 jωT [1.11] el factor anterior es debido al bloqueador el argumento de G es jωT − jωT 2 2 e jωT − 1 2 e 2 − e 2j ωT = = tan jωT jωT − jωT T e +1 T e 2 + e T 2 2 [1.12] la escala de frecuencias no es lineal. Por ejemplo si el sistema continuo no deja pasar una determinada frecuencia ω ′ , la frecuencia bloqueada en el discreto será ω′ = 2 ωT tan T 2 [1.13] o sea (ω ′T ) 2 2 − 1 ω ′T ω = tan ≈ ω ′ 1 − T 12 2 [1.14] No hay distorsión para ω = 0 y la distorsión es baja para bajas frecuencias. Para eliminar esta distorsión, a una determinada frecuencia ω1 se puede introducir una nueva transformación: s′ = tan ω1 ω1T ( 2 ) z −1 z +1 [1.15] ahora se cumple H ( e jω1T ) = G ( jω1 ) [1.16] para esa frecuencia son iguales, pero hay distorsión para otras frecuencias. Ejemplo 1.1. Integrador G (s ) = 1 s [1.17] su versión digital según Tustin Control Digital 08.doc 4 HT ( z ) = 1 T z +1 = 2 z −1 2 z −1 T z +1 [1.18] la versión modificada para ω1 HM ( z) = tan (ω T 2 ) z +1 1 ω1 [1.19] z −1 en función de la frecuencia H M ( e jωT ) = ( tan ω1T ω1 ) 2 e jωT + 1 = e jωT − 1 ( tan ω1T 2 ω1 ) 1 j tan ωT ( 2 ) [1.20] para ω = ω1 continua y discreta, coinciden. 1.1.3. Respuestas Equivalentes Se puede calcular una función de transferencia discreta para que tengan igual respuesta al escalón o a una rampa. Ejemplo 1.2. Comparación de Aproximaciones G ( s) = ( s + 1) (s + 5) 2 (s 2 2 (s 2 + 2s + 400 ) + 2s + 100 )( s 2 + 3s + 2500 ) [1.21] se muestrea con T = 0,03 s o sea ω N = 105 rad s con un bloqueador de orden cero resulta 1 Gˆ ( s ) = 1 − e − sT ) H ( e sT ) ( sT [1.22] Control Digital 08.doc 5 Bode Diagrams From: U(1) 0 -100 -150 100 0 To: Y(1) Phase (deg); Magnitude (dB) -50 -100 -200 -300 -1 10 0 1 10 10 2 10 3 10 Frequency (rad/sec) Sistema continuo, Aproximación de Tustin, BO0 Ejemplo 1.3. Motor con compensador en adelanto Motor: G ( s) = 1 s ( s + 1) [1.23] compensador en adelanto Gk ( s ) = 4 s +1 s+2 [1.24] función de transferencia en lazo cerrado Glc ( s ) = 4 s + 2s + 4 [1.25] 2 tiene un factor de amortiguamiento ξ = 0,5 y una frecuencia natural ω 0 = 2 rad s El objetivo es encontrar una función de transferencia que aproxime la respuesta en lazo cerrado según el esquema de la figura Control Digital 08.doc 6 ek r(t) uk CAD u(t) H(z) y(t) 1 s ( s + 1) CDA -1 La aproximación de Euler resulta z −1 +1 z − (1 − T ) z −1 + T H Ek ( z ) = 4 T =4 =4 z −1 z − 1 + 2T z − (1 − 2T ) +2 T [1.26] Tustin (2 −T ) 2 z −1 z− +1 (2 + T ) z − 2 + T (2 + T ) 2 +T HTk ( z ) = 4 T z + 1 =4 =4 2 z −1 ( 2 + 2T ) z − 2 + 2T 2 + 2T z − (1 − T ) +2 (1 + T ) T z +1 [1.27] La transformación con un bloqueador de orden cero del regulador resulta H BO 0 k ( z ) = 4 z − 2 (1 + e −2T ) z − e−2T =4 z − 0,5 (1 + e−2T ) [1.28] z − e−2T todas las aproximaciones tienen la forma Hk ( z ) = b0 z + b1 z + a1 [1.29] La frecuencia de corte del sistema continuo es ω c = 1,6 rad s y una buena elección del período de muestreo es T = 0,1L 0,3s 4 1.4 1.2 3 1 2 0.8 1 0.6 0 0.4 -1 0.2 -2 0 0 2 4 6 8 10 0 2 4 6 8 10 Discretización de Euler para diferentes períodos de Muestreo y el Control Continuo Control Digital 08.doc 7 1.3. Aproximación Basada en Variables de Estado La realimentación del estado puede verse como un controlador proporcional generalizado. Proceso dx = Ax + Bu dt y = Cx [1.30] se suponen medibles todos los estados Controlador u ( t ) = Mr ( t ) − Lx ( t ) [1.31] La versión discreta será % ( kT ) − Lx % ( kT ) u ( kT ) = Mr [1.32] Se trata de obtener las matrices aproximando las continuas El estado en lazo cerrado evoluciona dx = ( A − BL ) x + BMr = Alc x + BMr dt y = Cx [1.33] si la referencia se mantiene constante durante el período de muestreo se puede integrar en el período resultando xk +1 = Φ lc xk + Γlc rk [1.34] donde Φlc = e AlcT T Γlc = ∫ e Alc s dsB [1.35] 0 el controlador discreto deberá dar la misma respuesta, o sea ( ) % xk +1 = Φ − ΓL% xk + ΓMr k [1.36] donde Φ y Γ son las matrices en lazo abierto En general no es posible elegir L% tal que Φlc = Φ − Γ L% [1.37] Control Digital 08.doc 8 Se divide L% = L0 + L1 T [1.38] 2 Se puede hacer un desarrollo en serie ( ) 2 2 Φlc ≈ I + ( A − BL ) T + A 2 − BLA − ABL + ( BL ) T 2 +L [1.39] y Φ ≈ I + AT + A2 T ( ΓL% ≈ BT + AB T 2 2 2 2 +L [1.40] )( + L L0 + L1 T = BL T + BL T 2) 0 Φ − ΓL% ≈ I + ( A − BL0 ) T + ( A 2 − ABL0 − BL1 ) T 2 1 2 2 2 + ABL0 T 2 2 +L +L [1.41] [1.42] igualando término a término ( L% = L I + ( A − BL ) T 2 ) [1.43] Para calcular M se supone que en régimen estacionario las ecuaciones [1.34] y [1.36] deben dar el mismo valor según el continuo el valor final es ( I − Φlc ) x0 = Γ lc Mr [1.44] y en el discreto ( I − ( Φ − ΓL% ) ) x 0 % = ΓMr [1.45] suponiendo M% = M0 + M1 T [1.46] 2 Γlc M ≈ BMT + ( A − BL ) BM T 2 2 2 ΓM% ≈ BM 0T + ( BM 1 + ABM 0 ) T +L 2 [1.47] +L [1.48] esto da ( M% = I − LB T 2 )M [1.49] Ejemplo 1.4. Doble integrador. Aproximación de Realimentación del Estado Control Digital 08.doc 9 dx 0 1 0 x + u = 1 dt 0 0 y= 1 0 x [ ] [1.50] sea el controlador continuo u ( t ) = r ( t ) − [1 1] x ( t ) [1.51] se utiliza T = 0,5 las matrices discretas resultan L% = [1 − 0,5T 1] [1.52] M% = 1 − 0,5T [1.53] 1.2 1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 0 5 10 15 1.4. Métodos Basados en Respuesta en Frecuencia Bode y Nyquist son métodos frecuenciales adecuados para Sistemas expresados como entrada-salida. 1.1.4. Método de la Transformada w Pasos 1- Obtener una H ( z ) muestreando el sistema continuo con un BO0. 2- Definir la variable w = 2 z −1 . T z +1 3- Transformar H ( z ) obteniendo H ′ ( w ) = H ( z ) z =1+ wT 2 1− wT 2 4- Dibujar el Bode y utilizar los métodos convencionales. Control Digital 08.doc 10 5- Retransformar el controlador al plano z . Control Digital 08.doc 11