Lectura 2: TIPOS BÁSICOS DE INTERACCIONES FISICAS
Anuncio

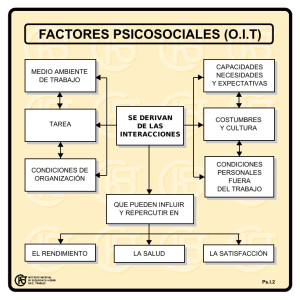
Actividad 4. ¿Cuántas clases distintas de fuerzas hay? La sección 5.5 del texto guía resume un inmenso caudal de información sobre las causas más recónditas de la actividad de la materia, obtenida en innumerables experimentos, desde las interacciones gravitacional y electromagnética, hasta las más misteriosas interacciones fuertes y débiles, muy alejadas de la experiencia cotidiana. Aunque el estudio formal de las interacciones electromagnéticas se hace en cursos más adelantados, en el presente curso es necesario abordar el tema sin ecuaciones para entender la respuesta a la pregunta planteada en el título y a la pregunta planteada al final del recuadro 3, que puede parafrasearse así, de manera antropocéntrica: ¿Cómo “sabe” la mesa que sostiene un objeto que “debe” ejercer sobre él una fuerza normal igual al peso del objeto para mantener a éste en equilibrio? Lo extraño de esta capacidad de la mesa para ajustar automáticamente el valor de la normal según la primera ley de Newton se pone de relieve cuando ponemos encima del objeto inicial un segundo objeto. Al parecer ello causa inmediatamente que la normal ejercida por la mesa se incremente en una cantidad igual al peso de este segundo objeto. Esta actividad es puramente conceptual, consistiendo esencialmente en el estudio de la sección 5.5 del texto guía, complementada con la lectura 2 y las exploraciones conceptuales contenidas en la última. Objetivo: El estudiante comprenderá la distinción entre interacciones fundamentales e interacciones derivadas, pudiendo explicar cualitativamente el origen de las fuerzas macroscópicas como manifestaciones colectivas estadísticas de las interacciones electromagnéticas entre las partículas constituyentes de los sistemas físicos (electrones y núcleos atómicos). Desarrollo de la actividad: Estudie la sección 5.5 del texto guía y la lectura 1, realizando las “exploraciones conceptuales” y verificando su comprensión mediante la discusión con sus compañeros sobre las preguntas, cuyas respuestas deben formar parte del portafolio del grupo. Lectura 2: TIPOS BÁSICOS DE INTERACCIONES FISICAS En la naturaleza y en la tecnología se producen incontables procesos de interacción de unas partes del universo con otras o entre sí. Es decir, influencias mutuas que alteran el estado físico-químico o biológico de la materia. Muchos de estos fenómenos complejos pueden ser simplificados y modelados, en ciertos aspectos, como interacciones entre un número reducido de partículas puntuales. Este es el caso en las situaciones estudiadas en esta unidad. Por ejemplo, usted está sentado ahora estudiando. Su cuerpo interactúa gravitacionalmente con la tierra, como sabemos en detalle a estas alturas del curso; además, interactúa con el asiento que evita su caída hacia el centro de la tierra. Ambas interacciones son de una naturaleza muy diferente, lo que comporta que su descripción matemática también lo sea. La primera se describe mediante una ley que establece la magnitud y dirección del vector peso. La segunda se describe mediante la fuerza normal, a la que tantas veces nos hemos referido. Pero, a diferencia de lo que sucede con la interacción gravitatoria, no existe una “fórmula” para la magnitud de esta fuerza (como ya dijimos en el recuadro 3, la ecuación n=mg no es una ley de la naturaleza, sino un resultado que ocasionalmente se obtiene, generalmente a partir de la primera ley de Newton). Sin embargo, en cierta forma la dirección de esta fuerza está determinada por una ley física: como su nombre indica, es perpendicular a la superficie soportante, oponiéndose al movimiento de penetración del objeto soportado. La Primera Ley de Newton, las dos “leyes” acerca de las direcciones de los vectores peso ⃗⃗⃗ y fuerza normal ⃗ , y los procedimientos del álgebra vectorial, nos permite establecer, en la situación en discusión (Usted en reposo sentado sobre una silla), la igualdad entre sus respectivas magnitudes (w = n). Haga explícitas todas las premisas y deducciones requeridas para llegar al anterior resultado, incluyendo la representación como cuerpos libres de su cuerpo, de la silla y de la tierra. Ahora bien, ¿cómo es posible que la silla aplique la primera ley tan exitosamente? No es posible responder esta pregunta, sin quedarse en fórmulas matemáticas que se aplican a ciegas, sin conocer algo sobre la naturaleza de la interacción que se describe mediante la fuerza normal. El objetivo de esta lectura es pues Actividad 4. ¿Cuántas clases distintas de fuerzas hay? ayudarle a entender la naturaleza de las interacciones más importantes involucradas en el curso. Al final volveremos a la pregunta, y comprenderá que además de la primera ley, hay una ley de la naturaleza implícita en la deducción de la relación entre el peso de un objeto en reposo y la normal que ejerce la superficie sobre la cual está apoyado. El diagrama que aparece en la siguiente página es un mapa conceptual, que clasifica las interacciones existentes en el Cosmos en una especie de árbol lógico. El mapa debe leerse empezando desde arriba. Las flechas indican las relaciones de inclusión entre las diferentes interacciones. Los conceptos de más bajo nivel, encerrados en óvalos más oscuros, corresponden a ejemplos de interacciones concretas observadas cotidianamente (ver figura 5.39 y la correspondiente leyenda). El texto siguiente explica el mapa. La primera división separa las interacciones en dos grandes tipos: las fundamentales y las derivadas o colectivas. Las primeras son las que tienen lugar entre las partículas elementales, los componentes “últimos” de la materia1: un protón con otro protón, con un neutrón, o con un electrón, etcétera. Las segundas son el efecto macroscópico resultante de las interacciones fundamentales presentes entre conjuntos enormes de partículas elementales. Es decir, son la combinación de interacciones entre los constituyentes de los cuerpos que observamos a las diversas escalas de tamaño, superiores a la escala de las partículas elementales: la escala nuclear, la escala atómica, la escala molecular, y así sucesivamente, hasta la escala del universo como un todo. Figura 1: Tipos de interacciones en la naturaleza Las interacciones fundamentales se dividen en dos subgrupos: las de corto alcance y las de largo alcance. Las primeras sólo se manifiestan directamente en la escala subatómica (de allí su designación). Se clasifican 1 La palabra „últimos‟ se pone entre comillas, pues bien podría suceder que en el futuro, cuando sea posible sondear la estructura de la materia en escalas submicroscópicas mucho más pequeñas de las que han podido ser estudiadas con los instrumentos científicos actualmente disponibles, se encuentre que los actuales componentes últimos están en realidad compuestos de otros componentes. UNIDAD 2: Predecir el movimiento MÓDULO 3: Aplicaciones de las leyes de Newton … Pág. 2 de 7 Actividad 4. ¿Cuántas clases distintas de fuerzas hay? a su vez en interacciones nucleares fuertes y débiles. Las reacciones de fusión termonucleares y la desintegración nuclear beta, mencionadas en el texto guía, son unos cuantos de los numerosos ejemplos de procesos naturales en la que ambas interacciones juegan un papel decisivo. Como ya sabemos, por la interacción fundamental de largo alcance llamada interacción gravitatoria, cualquier partícula elemental ejerce una influencia atractiva sobre todas las demás partículas elementales. Similarmente, por la interacción electromagnética ciertas partículas elementales, las partículas que tienen la propiedad carga eléctrica, ejercen influencia sobre las demás partículas eléctricamente cargadas, atractiva o repulsiva según tengan signos contrarios o iguales. Estas dos interacciones se hacen más pequeñas a mayor distancia, según la conocida ley del inverso al cuadrado descubierta por Newton, en el caso de la gravitación, y por Charles Augustin Coulomb (1736-1806), en el caso de un caso particular de la interacción electromagnética, la interacción electrostática. El peso de un cuerpo es la expresión de la interacción gravitatoria colectiva entre las partículas elementales que lo componen y las partículas elementales que componen nuestro planeta. Las interacciones electromagnéticas, tanto las que se presentan entre la partículas fundamentales consideradas individualmente como en sus manifestaciones colectivas macroscópicas, son muchísimo más complejas que las gravitatorias. La variedad de estas manifestaciones es tal que el cuadro presenta apenas unos pocos ejemplos de los que se estudian en los cursos introductorios de física. De hecho, salvo el peso, todas las demás fuerzas que han aparecido hasta ahora y que aparecerán en adelante son de naturaleza electromagnética. Las manifestaciones colectivas de la interacción electromagnética se dividen a su vez en dos grandes tipos. Por una parte, tenemos las que pertenecen a la clase de fuerzas que hemos llamado en el recuadro 3 “fuerzas activas”. Corresponden al significado habitual de la palabra „fuerza‟ en el lenguaje cotidiano, pues son las que generan el movimiento de los cuerpos de nuestra experiencia (por ello podrían llamarse también „fuerzas motrices‟). De hecho, el caso más prototípico de una fuerza activa es el peso, una fuerza no electromagnética, cuya magnitud y dirección están establecidas por la ley de la gravitación de Newton. En cambio, en otros casos el vector fuerza que representa la interacción puede fijarse arbitrariamente. Por ejemplo, la fuerza de tracción que acelera un automóvil, que proviene de la expansión de los gases producidos por la combustión de la gasolina en el motor, puede ser tan grande o pequeña como el conductor desee. Igual sucede con la contracción muscular (que también se origina en un conjunto de reacciones químicas en el interior de las células): si empujo contra una pared, puedo variar a voluntad la fuerza que ejerzo. Por otra parte, las manifestaciones colectivas de la interacción electromagnética que no son fuerzas activas pertenecen a la categoría de “fuerzas pasivas”, que introducimos en el recuadro 3. A diferencia de las activas, ni generan por sí mismas movimiento ni toman un valor fijado a voluntad o por una ley de la Naturaleza, sino que surgen transitoriamente en respuesta a la actuación de alguna fuerza activa presente en la situación, a la que se oponen de alguna manera (pero sin que se trate de un par “acción-reacción” de acuerdo a la tercera ley de Newton). Por ejemplo, la fuerza normal entre dos superficies sólidas en contacto y bajo presión, como la que está presente entre Usted y su silla2, es una fuerza electromagnética que surge en respuesta al movimiento de su cuerpo a medida que se hunde en la silla, cuyo valor se va incrementando hasta igual al peso y establecer el estado de equilibrio. Continuando con la explicación del mapa conceptual, observe la mitad inferior derecha. Las diferencias entre los tres tipos de fuerzas pasivas que aparecen en el mapa conceptual es consecuencia de las diferencias en la dependencia entre la magnitud de la fuerza pasiva y la de la fuerza activa a la que responde. En las fuerzas elásticas como la normal, que acabamos de mencionar, se trata de una estricta igualdad. En las fuerzas de resistencia al movimiento (que incluyen las fuerzas de fricción estática y dinámica y las fuerzas de resistencia en fluidos, estudiadas en la actividad 2) y en las fuerzas de empuje (una clase de fuerzas electromagnéticas derivadas presentes en los fluidos, que tienen cierta semejanza con la normal, y cuyo ejemplo prototípico es la fuerza que permite el vuelo de los aviones), la relación es muy compleja, como hemos visto para las primeras. Por el momento, para concluir la explicación de la figura 1, diremos una palabra más sobre las fuerzas elásticas, con el fin de que Usted pueda dar una respuesta con sus propias ideas a la pregunta planteada al 2 Es un error conceptual común en los novatos en física considerar que la normal y el peso forman un par acción – reacción como “manda” la tercera ley, debido a que tienen la misma magnitud y sentido opuesto (recuérdese el ejemplo conceptual 4.9 del texto guía, en que se aclara este malentendido) UNIDAD 2: Predecir el movimiento MÓDULO 3: Aplicaciones de las leyes de Newton … Pág. 3 de 7 Actividad 4. ¿Cuántas clases distintas de fuerzas hay? comienzo: ¿cómo es posible que la silla ajuste exactamente la fuerza que ejerce sobre Usted de acuerdo a la primera ley de Newton? La elasticidad es una propiedad muy familiar de algunos sólidos deformables. En el lenguaje cotidiano decimos que algo es elástico, por ejemplo una banda de caucho, porque después de estirarla, aumentando de manera apreciable su longitud, recupera su forma original luego de aflojarla. Pero en física la elasticidad incluye también la propiedad que tienen los “sólidos rígidos” de mantener su forma macroscópica en contra de las presiones y tensiones a las que pueden ser sometidos (dentro de ciertos límites). Veamos la figura 2. Un bloque es sometido a dos fuerzas de igual magnitud pero direcciones opuestas aplicadas a sus extremos. Decimos que este bloque está en tensión. Como resultado, sufrirá una deformación, es decir un cambio de longitud l. Si cuando se suspende la aplicación de las fuerzas el sólido vuelve a su longitud “en reposo”, decimos que el sólido es elástico bajo tensión. Sin embargo, generalmente l es una cantidad muy pequeña, tan pequeña que la deformación de la barra Figura 2 es prácticamente imperceptible, a menos que se utilice un equipo de muy alta sensibilidad. La figura 3 muestra un bloque en compresión. Nuevamente, la deformación l es una cantidad muy pequeña. El bloque será elástico bajo compresión si la deformación desaparece con la fuerza. Ahora bien, desde el punto de vista matemático la elasticidad significa, en ambas situaciones, que la magnitud es proporcional a la magnitud l. El coeficiente de proporcionalidad es una propiedad constitutiva característica de cada sólido que mide su “grado de elasticidad” (no haremos el estudio matemático preciso –el estudiante interesado lo encontrará en el capítulo 11 del libro). El hecho es que en la medida en que el sólido es más rígido (aunque sigue siendo elástico, en el sentido que tiene este concepto en la física) el “coeficiente de elasticidad” es mayor. En Figura 3 consecuencia, para una fuerza dada, la deformación será tanto menor; en el modelo ideal de un sólido “perfectamente rígido”, con un coeficiente de elasticidad que tiende a infinito, la deformación tenderá a cero (pero siempre habrá una deformación casi infinitesimal). La otra clase de fuerzas elásticas que nos presenta la figura 1 es la que corresponde a deformaciones macroscópicamente perceptibles, como la del ejemplo de la banda de caucho. El comportamiento de la deformación l en función de la fuerza de estiramiento F en este caso es complicado, pero en el caso de un resorte a veces el comportamiento es relativamente simple, pues nuevamente se observa una proporcionalidad directa entre ambas magnitudes. Cuando así ocurre decimos que el resorte tiene un comportamiento lineal, y “obedece” la ley de Hooke (que no es una ley de la naturaleza, sino un modelo empírico que los resortes reales a veces cumplen con cierta aproximación, y a veces no cumplen en absoluto). La constante de proporcionalidad en los resortes que obedecen esta ley, equivalente al coeficiente de elasticidad en los sólidos, se denomina “constante elástica del resorte” y se suele representar con la letra k (F=kl). La explicación del ajuste automático de las fuerzas pasivas es fácil en el caso de las fuerzas elásticas de tipo resorte, como la normal producida por una silla abullonada. El movimiento de descenso del cuerpo al sentarse va siendo progresivamente detenido al crecer la fuerza, en respuesta a la creciente deformación por compresión del cojín causada por ese movimiento. En el estado final de equilibrio la deformación del cojín será justo la requerida para producir una fuerza hacia arriba sobre el cuerpo, que compense exactamente el peso de éste impidiendo una mayor deformación. Pero ¿cómo se genera la normal que ejerce una mesa de piedra sobre un bloque colocado encima, en la que no se aprecia ninguna deformación macroscópica? La respuesta es que esta diferencia desaparece en lo esencial al examinar la estructura de la materia en la escala atómica, reduciéndose a diferencias en el coeficiente de elasticidad. La figura 4 (figura 18.17 del texto guía) muestra un modelo cualitativo simple de la estructura microscópica de los sólidos cristalinos, que explica sus propiedades elásticas, entre otras. Las esferas representan las moléculas (o átomos, según la sustancia) del sólido, y los resortes las fuerzas intermoleculares (interatómicas) electromagnéticas, que mantienen a los constituyentes del sólido vibrando alrededor de Figura 4 UNIDAD 2: Predecir el movimiento MÓDULO 3: Aplicaciones de las leyes de Newton … Pág. 4 de 7 Actividad 4. ¿Cuántas clases distintas de fuerzas hay? sus posiciones de equilibrio, de forma análoga a como vibra un peso suspendido de un resorte3. Cuando las moléculas de la mesa interactúan con las moléculas del bloque, los diminutos “resortes intermoleculares” se deforman análogamente a los muelles de un auto, aunque nuestra vista no percibe tal deformación. A mayor peso del bloque la deformación de la red atómica será consecuentemente mayor hasta restablecer el equilibrio, igual que sucede en el caso de la silla. Así pues, las fuerzas pasivas son la manifestación macroscópica y colectiva de un número enorme de interacciones electromagnéticas muy pequeñas de tipo resorte, lo cual les permite ajustarse dinámicamente a los requisitos de la situación. Exploración conceptual 1. Visualice y describa, usando el modelo de la figura 4, el proceso físico que origina la fuerza o fuerzas pasivas que actúan en las siguientes situaciones: 1. La lata de la figura 5 (en MCU, radio estable). 2. La bola en la figura 1, recuadro 3, actividad 3. 3. La caja en la figura 5.19 (b) y (c) del texto guía (pág. 173), Figura 5 que permanece inmóvil a pesar de la tensión aplicada 4. El deslizamiento a rapidez constante de la caja en la figura 5.19 (d) 5. La caja del problema de estudio 6, actividad 3, que permanece inmóvil respecto al camión cuando la aceleración de éste es menor que sg. 6. La situación descrita en el ejemplo conceptual 4.8 del texto guía, pág. 139. 7. El choque de dos bolas de billar, una de las cuales estaba en reposo. Exploración conceptual 2. Identifique cuáles de las fuerzas que han aparecido en el curso hasta ahora están presentes en la escena representada en la figura 6, y clasifíquelas en las categorías de la figura 1, agrupándolas en pares acción-reacción (3ª ley de Newton) y/o en pares fuerza activa/pasiva (a veces son coincidentes y otras no lo son). Figura 6 3 La modelación de la interacción entre los componentes últimos de las sustancias asimilándolas a fuerzas de resorte da cuenta del hecho de que los átomos (moléculas) se atraen si la distancia entre ellos es superior a una “distancia de equilibrio”, y se repelen si la distancia interatómica es inferior a la distancia de equilibrio. Este comportamiento es posible por el carácter atractivo de la fuerza eléctrica entre cargas opuestas y el carácter repulsivo de la fuerza eléctrica entre cargas iguales. En general, la relación entre la fuerza y la distancia interatómica no es exactamente de proporcionalidad directa, pero en primera aproximación se suele modelar como tal, al menos para explicar las propiedades elásticas de los materiales. UNIDAD 2: Predecir el movimiento MÓDULO 3: Aplicaciones de las leyes de Newton … Pág. 5 de 7 Actividad 4. ¿Cuántas clases distintas de fuerzas hay? Preguntas de comprensión 1. 2. 3. 4. 5. 6. 7. 8. 9. Haga un barrido de los términos clave de los capítulos 4 y 5, para verificar que todos los tipos de fuerza estudiados son clasificables en alguna de las categorías de la figura 1. Explique en sus propias palabras las diferencias entre fuerzas fundamentales y derivadas, y porqué es importante comprenderlas. ¿Qué implicaciones tiene el hecho de que las interacciones derivadas tengan un carácter colectivo? ¿En qué categoría clasificaría Ud. las fuerzas centrípeta y centrífuga? Explique en sus propias palabras las diferencias entre fuerzas activas y pasivas, y porqué es importante comprenderlas (por ejemplo, a la hora de resolver problemas de dinámica). ¿Cuál es la ley de la naturaleza que explica, junto con la primera ley de Newton (o la segunda, en algunos casos), el comportamiento de las fuerzas pasivas? ¿En cuáles de las situaciones contempladas en la exploración conceptual 1 el valor asumido por las fuerzas pasivas presentes está determinado por la segunda ley de Newton? ¿Por qué no existen fuerzas pasivas derivadas de la interacción gravitatoria? ¿Qué otras diferencias se puede esperar que existan entre las fuerzas pasivas y activas, desde el punto de vista de los intercambios de energía4? Autoevaluación del módulo A estas alturas del curso es de esperar que Ud. esté en condiciones de autorregular su propio aprendizaje. Es decir, Ud. ya tiene suficiente autonomía para decidir por su cuenta y riesgo el tiempo de estudio, las tareas de aprendizaje, determinar las medidas correctivas necesarias para subsanar posibles lagunas, etc. Por esta razón, es su plena responsabilidad autoevaluar su competencia en las técnicas de resolución de problemas de dinámica. Desde luego, el único procedimiento de autoevaluación de esta competencia es resolver exitosamente problemas representativos del nivel de dificultad del curso. A fin de facilitarle la selección de los problemas para su autoevaluación (a la vez que sigue aumentando su competencia), se señalan en el siguiente listado los problemas que, a juicio del autor de la unidad, no son representativos del nivel de dificultad del curso (pues exceden lo que cabe esperar razonablemente de la población de estudiantes a los que se dirige): 5.93, 5.96, 5.97, 5.102, 5.105, 5.106, 5.107, 5.120, 5.124, 5.125. Se sugiere seleccionar problemas tanto impares como pares; en caso de duda sobre la corrección del procedimiento en estos últimos es recomendable discutirlos con su grupo de estudio antes de plantear las dudas al profesor. 4 En la siguiente unidad se estudiará un aspecto esencial de las interacciones, que en muchas ocasiones van acompañadas de transferencia de energía, que como el estudiante recordará de sus cursos de ciencia en el bachillerato también cumplen una ley de conservación paralela a la de conservación de la cantidad de movimiento. UNIDAD 2: Predecir el movimiento MÓDULO 3: Aplicaciones de las leyes de Newton … Pág. 6 de 7 Actividad 4. ¿Cuántas clases distintas de fuerzas hay? AUTOEVALUACIÓN DE LA UNIDAD 1. 2. 3. Muestre que la ley de conservación de la cantidad de movimiento es equivalente a la Tercera Ley del movimiento de Newton Diseñe un mapa conceptual global con los conceptos básicos y fundamentales de la mecánica, y luego, en la medida en que lo considere necesario, diseñe mapas auxiliares que desarrollen más detalladamente algunos aspectos del sistema conceptual estudiado en esta unidad (entre los cuales se encontrarán obviamente los mapas que resumen la cinemática –ver autoevaluación de la unidad 1 y el de la figura 1 de la lectura 2). Resuelva los siguientes problemas, haciendo un análisis cuidadoso de las interacciones presentes de acuerdo a la actividad 4 del módulo 3 y de los supuestos necesarios, y explicando sus razonamientos según las pautas seguidas en los modelos de solución a los problemas propuestos: i) Un bloque de masa 12 kg se sostiene contra el techo mediante una fuerza ⃗⃗ de 160 N que actúa en un ángulo de 75° con la horizontal. Los coeficientes de fricción cinética y estática entre el bloque y el techo son 0.20 y 0.35. Calcule la aceleración del bloque (magnitud y dirección). (nota: la respuesta podría ser cero) M=12kg P 75° ii) Un vagón se acelera libremente al bajar por el plano inclinado de la figura. En el interior del vagón se fija una plataforma horizontal sobre la cual se coloca un bloque de masa m. a) Suponga que la superficie de la plataforma es perfectamente lisa. ¿Permanecerá el bloque en reposo, visto por un observador dentro del vagón? (en caso contrario, describa el movimiento observado). b) Si el bloque se desliza sobre la plataforma, ¿en qué dirección debería actuar una fuerza friccional sobre el bloque para impedir su deslizamiento? c) Ponemos el bloque sobre una báscula encima de la plataforma. ¿Cómo se compara la lectura de la báscula con el peso del bloque (es decir, será mayor, menor o igual)? d) Muestre que la fuerza friccional mínima que la superficie de la báscula debe ejercer sobre el bloque para impedir su movimiento respecto a la báscula es igual a mg sen cos , y que la lectura de la báscula será igual a mg cos2. Respuesta problema i): El bloque se acelera resbalando paralelamente al techo hacia la derecha a razón de 2,84 m/s2. UNIDAD 2: Predecir el movimiento MÓDULO 3: Aplicaciones de las leyes de Newton … Pág. 7 de 7