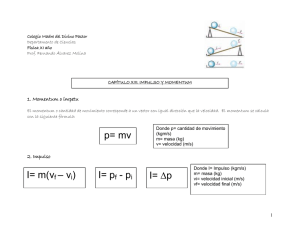
Módulo 3: Resolución de problemas con fuerzas impulsivas La
Anuncio

Módulo 3: Resolución de problemas con fuerzas impulsivas La primera ley de imposibilidad descubierta fue la conservación de la cantidad de movimiento. En la unidad 2 estudiamos este concepto, relacionándolo con la idea intuitiva del ímpetu, o “fuerza que mantiene el movimiento”. Los experimentos involucrados en la definición operacional de la masa se resumieron en la definición matemática de la cantidad de movimiento ⃗ como m⃗ y en la ecuación: (m1⃗ + m2⃗ 2)antes de la interacción = (m1⃗ 1 +m2⃗ 2)después de la interacción Esta ecuación vectorial constituye la ley de conservación de la cantidad de movimiento, generalizada a un número cualquiera de cuerpos en interacción mutua y sin interacción con otros cuerpos, reduciéndose a la primera ley de Newton cuando sólo hay un cuerpo en el sistema. Como nuestro interés era llegar a las leyes de Newton no explotamos la ley así obtenida para resolver situaciones donde es directamente aplicable, y en las cuales la segunda ley no es aplicable en la práctica por el desconocimiento de la fuerza que describe la interacción en función del tiempo. Es el caso de las colisiones, en las que la fuerza entre los cuerpos que chocan es de naturaleza impulsiva: una fuerza variable de muy alta intensidad y corta duración. En esta unidad añadiremos al arsenal de técnicas de resolución de problemas una nueva herramienta, que nos permite relacionar los vectores velocidad antes y después de la colisión. Si además la colisión es perfectamente elástica (lo que significa que los cambios de energía interna durante la colisión son reversibles y de hecho revierten, de modo que la energía cinética macroscópica después de la colisión vuelve a su valor original) disponemos de una ley de conservación adicional, permitiendo en algunos casos, en especial en colisiones rectilíneas, predecir todas las velocidades finales conociendo las iniciales. Objetivo: El estudiante desarrollará la competencia específica para analizar y modelar situaciones problemas en las que es aplicable la conservación de la cantidad de movimiento. Desarrollo del módulo 1. Estudie la introducción y las secciones 8.1 a 8.4, fijándose especialmente en las aplicaciones, puesto que el concepto de cantidad de movimiento y la ley de conservación ya son conocidos19. De hecho, las secciones 8.3 y 8.4 no son más que una ampliación detallada de la estrategia general para resolver problemas de la página 292, ejemplificándola a los dos tipos más sencillos de choques, los totalmente inelásticos y los perfectamente elásticos. El texto abunda en ejemplos resueltos; quizás podría dejar para más adelante los ejemplos 8.11 y 8.12, y el problema Evalúe su comprensión de la página 306, no por su dificultad matemática sino porque se sitúan en contextos muy poco familiares. El ejemplo 8.13 es de fácil planteo (como El concepto de impulso y el “teorema del impulso y la cantidad de movimiento” (sección 8.1) son algo análogos al concepto de trabajo y al teorema trabajo energía, pero tienen mucha menos importancia teórica y práctica que estos últimos y además son casi triviales desde el punto de vista matemático (el último se reduce a invertir la definición de fuerza como derivada temporal de la cantidad de movimiento). Por esta razón puede pasar rápidamente por esta sección. No obstante, reflexione con cuidado en la comparación conceptual y numérica entre cantidad de movimiento y energía cinética (dos combinaciones algebraicas distintas con las mismas magnitudes, pero con un significado físico muy diferente). 19 UNIDAD 3: Conservación y disipación de la energía Pág. 1 de 2 Módulo 3: Resolución de problemas con fuerzas impulsivas casi todos los problemas del capítulo) pero su álgebra es engorrosa (ver problema 8.41). Para desarrollar y evaluar su comprensión considere las preguntas P8.1 a P8.10, P8.12, P8.14 a P8.17 y los ejercicios 8.2, 8.5, 8.6, 8.8, 8.15, 8.19, 8.27 (este último es un caso particular del problema 2 de la pág. 76 del material estudiado en la unidad 2, La transformación en la explicación…), 8.32, 8.35, 20 2. Discusión en clase (3 horas) 3. Estudio de la sección 8.5 y continuación de la práctica de resolución de ejercicios21 y problemas de colisiones (problemas 8.58 a 8.9222, 8.101 y 8.102) y de localización y movimiento del centro de masa de un sistema de partículas (preguntas P8.18, P8.20, P8.22; ejercicios 8.44 a 8.50, y problemas 8.93 a 8.98). Note que las ecuaciones (8.28), o la ecuación vectorial equivalente (8.29) son definiciones matemáticas, cuya única justificación es la utilidad de las ecuaciones que se deducen de ellas y de otras ecuaciones ya conocidas; de hecho, las demás ecuaciones de la sección 8.5 son un desarrollo matemático de fácil comprensión que permite deducir cómo se mueve el centro de masa, el punto cuyas coordenadas son las calculadas mediante aquellas definiciones. El problema 8.100 le permitirá desarrollar ulteriormente su comprensión de este concepto al relacionarlo con el estudio de las colisiones y con la transformación de Galileo. 4. Discusión en clase y clase-taller (2 horas; véase el desarrollo del módulo 1, n.5 para el procedimiento de selección de problemas a discutir en el taller) Autoevaluación Resuelva los problemas 8.67, 8.74, 8.9423 20 R/ 8.6: magnitud: 1,09 kg m /s; dirección: -68,2° por debajo del eje X. 8.8: El impulso, o lo que es igual el cambio de la cantidad de movimiento, tiene magnitud 14,5 kg m/s; 7250 N. 8.32: a) El pequeño cambia su rapidez en 2,5 veces el cambio de rapidez del grande. 21 Los ejercicios 8.42 y 8.43 podrían ser omitidos en primera instancia. 22 Excepto el problema 8.83. Algunos problemas de este grupo pueden resolverse con mayor facilidad usando el concepto de centro de masa, aunque no se mencione explícitamente este término en el enunciado. En algunos problemas se menciona el término para referirse simplemente a la posición de la partícula que representa un cuerpo extenso (por ejemplo 8.72 y 8.78). Los problemas 8.69, 8.80 requieren un álgebra engorrosa. 23 R/ 8.74: 68.8°; 8.94: La canoa se mueve una distancia de 1,29 m hacia la izquierda. UNIDAD 3: Conservación y disipación de la energía Pág. 2 de 2 Módulo 3: Resolución de problemas con fuerzas impulsivas AUTOEVALUACIÓN DE LA UNIDAD Rediseñe el mapa conceptual global con los conceptos básicos y fundamentales de la mecánica realizado al concluir la segunda unidad, de modo que incluya los conceptos básicos introducidos en esta unidad. Responda la pregunta esencial de la unidad Resuelva los siguientes problemas, haciendo un análisis cuidadoso de las interacciones presentes de acuerdo a la actividad 4 del módulo 3 de la segunda unidad y de los supuestos necesarios, y explicando sus razonamientos según las pautas seguidas en los modelos de solución a los problemas propuestos en las primeras dos unidades del curso. 1. Una persona está en reposo sobre un piso duro y desea saltar verticalmente, elevando su centro de masa a una altura lo más grande posible. a. ¿Cómo debe proceder y por qué (explique en lenguaje cotidiano)? b. Analice el fenómeno dinámicamente (esto es, desde el punto de vista de la conservación de la cantidad de movimiento y considerando las fuerzas presentes en el sistema, que Usted debe definir apropiadamente) c. Analice el fenómeno energéticamente 2. Problema 8.101 3. Problema 8.103 (Explique físicamente la respuesta a la parte (b), sin limitarse a los números) Autoevaluación de la unidad Pag 1/1