DINÁMICA (movimiento bajo la acción de fuerzas) Interacción de la

FÍSICA – DINÁMICA Y GRAVEDAD
39
DINÁMICA (movimiento bajo la acción de fuerzas)
Fuerza
Vimos que para explicar los cambios en el estado de reposo o movimiento
uniforme de la materia se utiliza en física el concepto de fuerza, del que nos
da una medida intuitiva el esfuerzo muscular que hacemos para mover
algo, o la sensación de presión cuando sostenemos algo pesado. También
se dijo que las fuerzas siempre actúan de a pares, es decir que ante una
acción (fuerza x tiempo) existe siempre la correspondiente reacción equilibrante.
Masa
Recordemos que masa es una propiedad de la materia representada por
una cantidad escalar m cuya unidad es el Kg. Esta unidad corresponde muy
aproximadamente a la masa de un litro de agua en condiciones normales de
temperatura y presión . Cuando un cuerpo de masa unitaria invariable en el
tiempo (1 Kg) sufre una aceleración unitaria (1 m/s2) es porque actúa en el
sentido de ésta una fuerza unitaria igual al producto entre ambas, o sea 1
Kg.m/s2 = 1 N (se lee “un Newton”)
Cantidad de movimiento
Se llama cantidad de movimiento de un cuerpo material de masa m que se
mueve a la velocidad v al vector resultante del producto m·v. Si la masa del
cuerpo no varía en el tiempo, como ocurre en la mayoría de los casos, la
variación de la cantidad de movimiento ∆(mv) en un lapso ∆t es igual a m·∆v
y coincide siempre con la acción de una fuerza f durante el mismo lapso ∆ t
tal que m ∆v=f.∆t .
m2
Interacción de la materia
m1
v2i
m1.v1f
v1i
m1
x2
-x1
Ley de conservación de la cantidad de movimiento
m1.v1i
m2 m2.v2f
m2.v2i
O
Q
P
INTERACCIÓN
POR CHOQUE
Cuando un conjunto de varios cuerpos
interaccionan a través de acciones directas
(choque) o fuerzas a distancia, la experiencia demuestra que a lo largo del tiempo se
conserva siempre la cantidad de movimiento total, expresada como la suma
FÍSICA – DINÁMICA Y GRAVEDAD
40
vectorial de la cantidad de movimiento individual de cada uno de los cuerpos
del sistema. Este principio de conservación de la cantidad de movimiento es
absolutamente general y no conoce excepciones.
Interacción entre cuerpos
La experiencia demuestra que cuando dos o más cuerpos chocan entre sí, la
cantidad de movimiento total del sistema antes y después del choque se
conserva, de acuerdo a lo dicho recién. De tal manera, si dos cuerpos de
masa m1 y m2 que tienen velocidades iniciales v1i y v2i y al cabo de un lapso
1
durante el cual interactúan quedan con velocidades finales v1f y v2f, podemos plantear la igualdad vectorial siguiente:
m1.v1i + m 2.v2i = m1.v1f + m2.v2f de donde m1.(v1i-v1f) = m2.(v2i-v2f)
En el dibujo se representan las posiciones sucesivas y el diagrama vectorial
con la ecuación de cantidades de movimiento.
Centro de gravedad de un sistema de masas
Se ve en la figura que es nula la proyección de la resultante de los vectores
cantidad de movimiento sobre una perpendicular PQ a su dirección, lo que
responde a la ecuación m1.(-x1)/t = m2.x2/t , tomando las distancias x con su
signo de acuerdo al sentido del vector trazado desde el origen O
De la anterior se deduce que para cualquier instante t es m1.x1+m2.x2=0 ,
igualdad que es útil interpretar reconociendo que en un sistema de masas
existe en todo momento un punto O que se llama centro de masas, centro
de gravedad o baricentro del sistema de masas, para el cual es nulo la
suma del producto de las masas por las respectivas distancias a dicho punto.
Esa suma de productos se llama “momento de primer orden” de la distribución de masas con respecto al punto de referencia. En el caso de que ese
punto sea el centro de gravedad, el momento de primer orden es nulo.
El movimiento del centro de masas de un sistema sobre el que no actúen
acciones exteriores no se altera a lo largo del tiempo, cualquiera sea el tipo
de interacción entre las masas del sistema. Se ve en la figura que O se desplaza con velocidad uniforme V correspondiente a un cuerpo de masa
M=m1+m2 con cantidad de movimiento MV = m1.v1 + m 2.v2 tal que
V= (m1.v1 + m2.v2) / (m1+m2)
1
La interacción puede ser choque o fuerzas a distancia, como la gravitación o la
acción electrostática. Las teorías modernas tienden a reducir estas últimas a efectos
estadísticos de infinidad de choques de partículas elementales, que se intercambiarían
entre sí los cuerpos que se atraen o repelen a la distancia.
FÍSICA – DINÁMICA Y GRAVEDAD
41
Acciones de las fuerzas
Fuerzas exteriores e interiores a un sistema de masas
Podemos dividir a las fuerzas que actúan sobre un sistema de cuerpos en
fuerzas exteriores e interiores. Las fuerzas exteriores son las responsables de la aceleración del centro de gravedad del sistema o conjunto de
masas, y tienen su origen en interacciones con otros cuerpos no pertenecientes al sistema. Las interiores se generan por interacciones entre los
elementos del sistema y tienen resultante nula, debido al principio de acción y reacción.
Jugando al billar – Primera parte
Entremos al salón “Bar-Billares” del barrio, donde encontramos una mesa de
billar con 2 bolas iguales de masa m b =1 Kg colocadas a 0,5 m de distancia,
quietas sobre el tapete. Consecuentemente su centro de gravedad, en el
punto medio de la recta que une los centros de ambas bolas, a 0,25 m de
cada una, también está inmóvil.
o
vbi
a
v2
v1
v
Trayectoria del centro de
gravedad del sistema
o
vo
v1
v
v2
Tomemos el taco (sistema exterior)
y aplicamos un tacazo sobre la bola
Nº1 de masa m b=1Kg , que adquiere una velocidad de traslación vb =
0,25 m/s dirigida hacia la bola Nº2
Esa primera bola (roja) avanza con
aceleración negativa a (en sentido
contrario a la velocidad), ya que el
paño ejerce sobre ella una fuerza
de rozamiento constante en contra
del movimiento fr = 0,05N. Al cabo
de recorrer 0,25 m choca contra la
segunda bola (azul).
v=
o velocidad del
centro de gravedad
¿A qué velocidad v hace impacto?
Si fr=0,05 N es a = fr/m b = 0,05/1= 0,05 m/s2
y entonces vbfinal=vbinicial-a.t , recorriendo una distancia d= ½ a.t2 de donde
t=(2d/a)½ con lo cual
v=vbi-(2d.a)½ = 0,25-(2x0,25x0,05)½ = 0,092 m/s
Supongamos ahora que esa primera bola a velocidad de 0,092 m/s impacta
sobre la segunda bola. Como consecuencia del choque la segunda bola
tomará una velocidad v2 y la primera pasará a v1.
FÍSICA – DINÁMICA Y GRAVEDAD
42
La reacción en el choque siempre se lleva a cabo en la dirección entre centros de esferas, donde está el centro O de gravedad del sistema.
Si dicha dirección coincide con la de la velocidad inicial v de la bola, las
reacciónes m1.v1 y m2.v2 están también sobre ese eje. Este fenómeno unidimensional se llama “choque recto”
Si la dirección del eje que une centros de esferas no coincide con la velocidad, el fenómeno es un “choque oblicuo”, como el que se ha representado
en los dibujos adjuntos. En él las velocidades v1 y v2 tienen diferentes direcciones
La cantidad de movimiento del sistema antes del choque es m b.v , y es igual
a la cantidad de movimiento del sistema después del choque m b.v1+mb.v2 .
Cuando las dos bolas tienen la misma masa, resulta v =v1+v2
Hay infinitas maneras de equilibrar el vector velocidad v con v1 y v2. En el
dibujo se ha elegido tentativamente un par de valores que satisfacen las
leyes de la conservación del impulso, que no son necesariamente los que se
dan experimentalmente. Para determinar las velocidades reales hace falta
conocer lo que se explicará a continuación sobre trabajo y energía.
Efectos de las fuerzas
La acción de una fuerza sobre un cuerpo material se traduce en varios efectos, que pueden coexistir:
a) Variación de la cantidad de movimiento
b) Presión acompañada generalmente de contracción
c) Tensión acompañada generalmente de dilatación
Si el cuerpo no se mueve, o se mueve con aceleración menor que la que
resulta del cociente fuerza/masa, es porque la acción está equilibrada total o
parcialmente por una interacción con otro cuerpo o sistema. Si ese segundo
cuerpo tiene una masa comparativamente mucho mayor que el estudiado, y
la interacción se hace a través de un medio rígido (un tercer cuerpo o agente
indeformable), no habrá movimiento del conjunto y se dice que el sistema
está en equilibrio estático. Si el medio por el que se efectúa la interacción no
es rígido, por ejemplo fluido, permitirá que la acción de la fuerza se manifieste en una variación de la cantidad de movimiento
Por ejemplo, si aplicamos una fuerza F = 1 N a un carrito de masa m = 2 Kg apoyado
sobre el suelo, éste se moverá con una aceleración a’ menor que la que corresponde
2
a una masa libre a = F/m = 0,5 m/s , por ejemplo a’ = 0,45 m/s2 . La diferencia de
aceleraciones se debe a una fuerza que vale f = m. (a-a’) = 2x0,05 = 0,1 N
FÍSICA – DINÁMICA Y GRAVEDAD
43
Estudiaremos luego que en los vehículos que ruedan , f tiene tres orígenes:
•
el rozamiento en ruedas y cojinetes, del que hablaremos más adelante.
•
la inercia a la aceleración angular de las ruedas
•
la resistencia del aire.
Trabajo de una fuerza
Cuando una fuerza se aplica a lo largo de una trayectoria se ejecuta un
2
trabajo
Trabajo de una fuerza variable f
a lo largo de una trayectoria AB
T = Σ fi · dsi
fn
El trabajo de una fuerza que se
desplaza por una trayectoria se
mide por el producto escalar entre
fi
el vector representativo de la fuerf3
za y el vector representativo de la
f2
f1
distancia recorrida. Si el camino es
recto de longitud AB y la fuerza f es
dsi
constante en intensidad y dirección, el trabajo entre los puntos A y
A
B está representado por el producto escalar T = f·AB = f.AB.cos(α
α), siendo α el ángulo formado por la
dirección de f y la de AB
B
Si la trayectoria tiene forma cualquiera, para una fuerza constante o variable
a lo largo de ella, el trabajo total entre sus extremos se calcula dividiendo el
camino en pequeños trozos i numerados de 1 hasta n , de longitud elemental dsi suficientemente pequeños como para que se puedan considerar rectos y con una fuerza respectiva fi aplicada a lo largo de cada uno de ellos ,
de manera que el trabajo total sea la suma de n trabajos elementales. En
ese caso es T = Σ (fi·dsi) para i=1,2...n
Energía de un sistema
El trabajo se mide en unidades de energía, función que representa la capacidad de ejecutar trabajo de un sistema. La unidad de energía está representada por el trabajo de una fuerza unitaria a lo largo de un camino recto de
su misma dirección y de longitud también unitaria. En el sistema MKS la
unidad es el Joule, en honor al físico inglés J.P.Joule (1818-1889). Así una
fuerza unitaria de 1N a lo largo de una distancia de 1m ejecuta un trabajo de
1Nm=1J (se lee un Newton por un metro es igual a un Joule)
2
El concepto de trabajo recién enunciado, difiere del que se le da en lenguaje corriente, en el que está ligado a esfuerzo y dificultad antes que a un desplazamiento de
una fuerza. Sostener un peso “da trabajo”. Sin embargo desde el punto de vista físico,
no hay trabajo si no subimos o bajamos ese peso.
FÍSICA – DINÁMICA Y GRAVEDAD
44
Tipos de energía
De lo visto se entiende que trabajo y energía son conceptos asociados a
sistemas materiales. No se puede pensar en energía y trabajo ejecutado sin
un soporte material desde dónde salga y otro soporte de destino hacia donde
vaya. El soporte material aludido comprende materia y espacio que la rodea.
Las propiedades del espacio, por ejemplo la de transmitir fuerzas a distancia,
son producto de la materia próxima, como se verá al tratar la gravitación.
Un sistema material puede poseer capacidad de ejecutar trabajo de varias
formas, pero éste se manifestará siempre a través de una fuerza que se
mueve a lo largo de un camino. El trabajo ejecutado por un sistema siempre
se efectúa sobre otro u otros sistemas. El primero perderá energía y los
segundos la recibirán, y desde ese punto de vista el trabajo puede considerarse como flujo de energía o energía en tránsito. El trabajo no es la única
forma de energía en tránsito. Existe otra: el calor, que puede considerarse
macroscópicamente como un fluído, o microscópicamente como una función
estadística asociada a la energía de movimiento de las moléculas o partículas que componen la materia.
Energía cinética - Teorema de la fuerza viva
Vimos que una de las manifestaciones de una fuerza es la variación en el
movimiento de la materia en la que se aplica. La fuerza aplicada desde otro
sistema sobre una partícula material de masa m es igual a la variación de la
cantidad de movimiento:
f = d(mv)/dt , y si la masa m no varía con el tiempo será f = m.dv/dt = m.a
También es m.dv=f.dt (acción o impulso)
Si la acción se desarrolla a lo largo de un camino de longitud dx , el trabajo
ejecutado por la fuerza sobre la masa m será f.dx=m.dv/dt.dx .
Pero como v=dx/dt , la anterior queda en la forma f.dx=m.v.dv
Eso nos dice que el en un pequeño recorrido dx la fuerza f sobre un sistema
de masa m efectuará un trabajo f.dx que será igual al aumento de energía
del sistema m.v.dv , siendo dv el aumento de velocidad en un pequeño intervalo de tiempo dt.
En un mayor intervalo de tiempo ∆t = t2-t1 la fuerv1
za f recorrerá un camino ∆x = x2-x1 a una velocidad promedio igual a vm = (v2+v1)/2 para ∆v = v2v2
m
v1 , y el trabajo de la fuerza f (que supondremos
∆x
constante a lo largo del camino ∆x) será:
m
T = f.(x2-x1)= m.vm.∆v = ½ m (v22-v12) =
2
2
= [½ m.v2 – ½ m v1 ]
FÍSICA – DINÁMICA Y GRAVEDAD
45
Es decir que el trabajo de la fuerza exterior aplicada a la partícula de masa
m es una diferencia de términos iguales a la mitad del producto de la masa
por la velocidad al cuadrado Ec = ½ m v2 . Esa cantidad Ec debe considerarse como la energía asociada a la velocidad v. Se llama a Ec energía
3
cinética o fuerza viva de una partícula de masa m en movimiento .
Lo anterior nos dice el trabajo de una fuerza exterior sobre una partícula
material es igual a la variación de su fuerza viva . Este enunciado se conoce
como “Teorema de la fuerza viva”
Cuando se habla de fuerzas exteriores, se entiende que son exteriores al
sistema de referencia, y que provienen de otro u otros sistemas, que puede
ser el resto del universo o una porción limitada de éste.
Energía potencial
Definida como la capacidad de un sistema de desarrollar trabajo, la energía
puede estar almacenada en la forma o configuración del sistema. Un resorte
comprimido y un sistema de dos masas alejadas son dos ejemplos de sistemas que poseen energía de forma que puede ser transformada en fuerza
viva u otro tipo de energía, y que pueden ejercer trabajo sobre otro sistema.
El resorte puede dar fuerza viva al percutor de un arma. Una pesa elevada a
una altura conveniente mueve en su descenso a un molinete sumergido,
elevando la temperatura de una masa de agua (experiencia de Joule en
1843 para encontrar el equivalente mecánico del calor).
Sistemas de fuerzas conservativas
Podemos imaginar que la energía de configuración de los sistemas descriptos proviene del almacenamiento del trabajo de una fuerza exterior que llevó
el sistema desde una cierta configuración inicial a la configuración final. La
fuerza o fuerzas exteriores pudieron haber hecho el trabajo de compresión
del resorte o la subida del peso por varios caminos y en diversos tiempos.
Sin embargo, la energía almacenada sólo depende del trabajo de una fuerza
a la que es posible asignar un valor a cada posición posible del sistema, por
ejemplo a la altura del peso, o a la longitud del resorte.
En tales casos el sistema tiene asociado un conjunto de fuerzas dependiente
de la posición o configuración, y la energía de configuración sólo es función
de la posición inicial y final.
Se designa a tal conjunto de fuerzas y su distribución en el espacio como
“campo de fuerzas conservativo”, justificándose el adjetivo “conservativo” por
3
Nótese que el cuadrado del vector v es un escalar v
2
FÍSICA – DINÁMICA Y GRAVEDAD
46
las razones que explicaremos luego.
Un campo de fuerzas conservativo admite un modelo de relieve topográfico
que se desarrollará con todo detalle al estudiar la gravedad y el campo gravitatorio, y que ahora sólo esbozaremos. En este modelo las líneas de fuerza
(envolventes de las direcciones de las fuerzas en el espacio) equivalen en
un mapa de relieve a las líneas de máxima pendiente que nacen en las cumbres bajando perpendicularmente a las líneas de nivel o altura sobre el nivel
del mar. El equivalente energético de esa altura es el potencial, cuyo gradiente o máxima pendiente en cada lugar es precisamente el valor del campo en ese punto, que representa a la fuerza de deformación en el caso del
resorte o la de la gravedad en el caso del peso que se eleva.
La diferencia de potencial entre dos puntos es el trabajo mínimo necesario
para deformar o configurar el sistema yendo desde la primera posición a la
segunda en una evolución en equilibrio.
El valor de ese potencial (escalar) está en relación directa con la densidad
de líneas de campo. Líneas divergentes corresponden a un campo que se va
debilitando, y un campo de líneas convergentes indica que la fuerza crece
hasta tener un valor infinito en el punto de convergencia. En ambos casos el
potencial correspondiente recuerda a un monte con el pico en el punto de
convergencia. Un campo de fuerzas de líneas paralelas corresponde a una
fuerza constante en todo el espacio. El campo paralelo admite un potencial
en forma de rampa rectilínea (caso de la fuerza de gravedad en un modelo
que desprecia la curvatura de la tierra).
Las líneas de fuerza brotan en las fuentes de campo y se sumen en los sumideros de campo. En el campo eléctrico las fuentes y sumideros son las
cargas positivas y negativas respectivamente. El campo gravitatorio tiene
sus sumideros de campo en las masa materiales , metidas en un mar infinito
que no requiere fuentes. Fuera de las fuentes o sumideros, o sea en el es4
pacio vacío, se conserva el número de líneas de campo . De allí que a estos
campos se los designe como conservativos y a las fuerzas correspondientes
“fuerzas conservativas”.
Sistemas de fuerzas NO conservativas
Vimos que las fuerzas conservativas son desde el punto de vista matemático
el gradiente vectorial de una función que asigna a cada punto del sistema un
potencial escalar. Hay sistemas que no tienen una respuesta tal que las
fuerzas puedan derivarse de un potencial con valor fijo para cada punto del
espacio.
4
En una superficie cerrada que no contenga fuentes ni sumideros en su interior entran
y salen el mismo número de líneas de campo. Matemáticamente hablando, es nulo el
flujo de campo en una superficie cerrada (Véase luego “Ley de Gauss”)
FÍSICA – DINÁMICA Y GRAVEDAD
47
Si en vez de un resorte elástico que recupera su forma al soltarlo, comprimimos una
bola se goma cruda (masa semiplástica), la deformación no estará acompañada de un
esfuerzo proporcional a la misma y según el sentido y la velocidad de la deformación
impuesta, variará la fuerza en cada punto de la trayectoria de deformación. Por lo
tanto tampoco se recuperará todo el trabajo de deformación. Se dice que estos materiales poseen memoria de forma, ya que conservan más o menos en su forma actual
la deformación impuesta en el pasado.
Otros ejemplos típicos de fuerzas no conservativas son las resistencias al
deslizamiento y la rodadura entre sólidos, la resistencia viscosa que presentan los fluídos al movimiento de sólidos en su seno y las fricciones internas a
nivel molecular en el interior de los sólidos.
El rozamiento o fricción es un fenómeno que se explica a nivel microscópico por la interferencia de las rugosidades superficiales de cuerpos en contacto con movimiento relativo. En gran medida la fuerza tangencial resistente
que produce este efecto depende de la presión entre superficies y el estado
de éstas. Este fenómeno será estudiado con más detalle al tratar el tema
de la estabilidad de sistemas.
La resistencia viscosa es proporcional a la velocidad relativa entre sólido y
líquido está ligada a la propiedad de los fluídos de trasmitir fuerza tangencial
con el movimiento de sus partículas, y que será estudiada al tratar la estructura y propiedades mecánicas de los fluídos.
Sistemas que evolucionan con desarrollo de fuerzas resistentes no conservativas transforman el trabajo de dichas fuerzas en energía térmica, que se
manifiesta por el aumento de la temperatura de la materia de los sistemas
involucrados. En los títulos siguientes ampliaremos este tema.
Principio de conservación de la energía - Calor y Termodinámica
La transferencia de energía entre sistemas se realiza mediante evoluciones
(cambios sucesivos) que afectan a los sistemas dador y receptor.
Por ejemplo, al comprimir un resorte con nuestra fuerza muscular, ejercemos una
acción sobre el objeto, entregando energía. Ella se transfiere en parte a través del
trabajo de la fuerza aplicada al resorte, que se deforma.
El fenómeno descripto se realiza en el tiempo y en el espacio, afectando no sólo la
forma sino también el estado de los sistemas: nuestros músculos que se mueven a
costa de quemar reservas de glucosa, grasas, etc, Estas oxidaciones producen energía muscular que se transfiere y energía térmica que termina disipándose en el ambiente. Mientras tanto el resorte cambia de forma cuando la fuerza ejercida por nuestro
brazo lo comprime, reteniendo así energía de configuración. Dependiendo de la mayor
o menor velocidad en esta compresión y de la estructura del material, una mayor o
FÍSICA – DINÁMICA Y GRAVEDAD
48
menor parte de el trabajo entregado se transformará también en calor dentro del resorte, elevando su temperatura. Esa energía térmica generada por fricción molecular
en el acero, no contribuye a la deformación y no estará dentro de la energía que el
resorte está en condiciones de devolver al distenderse a posiciones anteriores, cuando
la fuerza de compresión disminuya.
Es un hecho ampliamente comprobado que la energía total al principio durante y al final de la evolución entre dos o más sistemas que intercambian
energía se mantiene sin pérdida, aunque puede cambiar de tipo dentro de
cada sistema durante la transformación.
Consideremos por ejemplo un sistema formado por una gran cantidad de
partículas que interactúan entre sí. Si bien en teoría podríamos considerar a
cada partícula como un cuerpo independiente, y estudiar su evolución a
partir de sus posiciones y velocidades a partir de un cierto instante, en la
práctica es ventajoso estudiar al conjunto asignándole propiedades globales
y reemplazar las propiedades particulares de cada elemento por promedios
estadísticos. Así entonces:
La energía potencial V del sistema está dada por el trabajo para llevar el
sistema de masa total M a la altura h de su centro de gravedad sobre el
plano de referencia (el nivel del mar, por ejemplo, al que se asigna altura
cero) V=M.g.h
La energía cinética Ec será igual al trabajo de las fuerzas exteriores sobre
el conjunto del sistema, que lo acelera desde el reposo hasta la velocidad v
(es la velocidad del centro de gravedad) Ec = ½M.v2
La energía interna U de un sistema formado por i partículas de masa m i a
velocidades relativas al centro de gravedad vi es la suma de la energía cinética de todos ellos U = ½Σ
Σmi.vi2 , y es diferente de Ec = ½M.v2 que es la
energía cinética o fuerza viva del conjunto de masa M = Σ mi cuyo centro de
gravedad se mueve con velocidad v
Se puede plantear entonces así la siguiente ecuación:
Energía potencial + Energía cinética + Energía interna = constante
V + Ec + U = cte
Este principio, de conservación de la energía, junto con el de conservación de la
masa se han fusionado en el principio único de conservación de la masa-energía,
en virtud de la incorporación de conceptos de electromagnetismo a la mecánica clásica ocurridos a fines del siglo pasado. De este tema ya se ha hablado en este libro y se
lo trata extensamente en el libro de óptica. La diferencia entre aplicar el principio integrado de conservación de masa-energía o aplicar los principios de conservación de la
masa y de la energía separadamente por el otro, tiene sólamente importancia cuando
están en juego grandes velocidades, que no es el caso de los ejemplos de esta sección de la obra.
FÍSICA – DINÁMICA Y GRAVEDAD
49
Cuando se aplica a un sistema que intercambia energía con otro u otros, se
puede plantear que la energía perdida por el primero es ganada por el o los
otros a través de una transferencia de energía en forma de trabajo L y en
forma de flujo calórico o sencillamente calor ∆Q:
∆V + ∆Ec + ∆U = L + ∆Q
Queda así definido el calor por exclusión, como una forma de energía en
tránsito que NO es trabajo.
Esta conclusión del principio de conservación de la energía es el punto de
arranque o “primer principio” de la Termodinámica, ciencia que incorpora en
las ecuaciones y balances energéticos esta nueva forma de energía en tránsito, el calor.
Calor y trabajo tienen unidades de energía. Se puede transformar trabajo en calor,
entregando el primero a un sistema no conservativo.
El estudio del aprovechamiento del flujo de calor para obtener trabajo llevó al ingeniero
militar francés Sadi Carnot en 1820 a plantear por primera vez y cuantificar esta ley
inexorable de la Naturaleza: la transformación de calor en trabajo requiere dos sistemas de diferente temperatura o “nivel térmico”: una fuente caliente y una fuente fría.
5
Esa diferencia de nivel junto con el valor absoluto de la temperatura más baja limita el
rendimiento de dicha transformación.
La incorporación de los principios de termodinámica en todos los capítulos de la física
es una necesidad de la que esta obra se hace cargo, para comprender mejor una gran
cantidad de temas, especialmente los que se refieren a transferencia de energía e
información.
Se estará en condiciones de entender mejor el significado del segundo principio después de estudiar sistemas gaseosos y sus leyes.
Jugando al billar – Segunda parte
Estamos nuevamente en nuestro “Bar–Billares” del barrio, resueltos a estudiar a fondo las leyes físicas del juego. Recordemos que con la igualdad
vectorial que se deduce del principio de conservación del impulso m b.v =
m b.v1+mb.v2 , no es posible determinar el par de valores que realmente se
da en la realidad, entre las infinitas combinaciones de velocidades v1 y v2
cuya suma vale v , .
En ese cometido, apliquemos el principio de conservación de la energía
5
La temperatura absoluta es una medida de la energía interna de un cuerpo. Su
significado preciso se dará al estudiar sistemas gaseosos.
FÍSICA – DINÁMICA Y GRAVEDAD
50
además del de la conservación del impulso al sistema material que sufre el
choque.
Choque elástico y plástico
Según reconoció Newton en el siglo XVII al estudiar el choque de cuerpos, éstos se
deforman durante el impacto.
Depende de la elasticidad de los cuerpos involucrados que la energía potencial de
deformación sea devuelta totalmente, parcialmente o no se devuelva en absoluto al
sistema .
Estas tres posibilidades distinguen tres tipos de choque: el elástico, el semi-elástico
y el plástico.
Coeficiente de restitución
La energía que puede obtenerse desde adentro de un sistema de dos masas m1 y m2
a velocidades diferentes v1 y v2 es en general menor que la suma de las energías
cinéticas de cada una de las masas, que es la que presenta el sistema para un observador en reposo exterior al mismo. Esto es así ya que acciones desde el interior del
sistema no pueden afectar el movimiento del centro de gravedad, que como vimos
siempre se mantiene a velocidad constante v0= (m1.v1 + m2.v2) / (m1+m2) (antes,
durante y después de la interacción) mientras no actúen fuerzas exteriores.
De tal manera, colocándonos en el centro de gravedad del sistema formado por las
masas m1 y m2 , cuyas velocidades relativas con respecto a ese punto son (v1-v0) y
(v2-v0) respectivamente, podremos extraer una energía interna Ei tal que
2
2
2
2
Ei = ½ m1(v1-v0) + ½ m2(v2-v0) = ½ m1.v1 + ½ m2.v2 - ½ (m1+m2) v0
2
Se ve que la energía aprovechable desde el interior del propio sistema es la suma de
las energías cinéticas individuales de cada una de las masas, menos un término (el
tercero) que corresponde a la energía retenida por el sistema de masa total
M=m1+m2 , que se mueve a la velocidad v0 que posee el centro de gravedad en todo
momento.
La energía interna Ei puede transformarse en deformación elástica, semi-elástica o
plástica. La relación entre Ei después y antes del choque es un número llamado “coeficiente de restitución, que toma valores entre cero y uno:
cr= Ei’/Ei para 0<=cr<=1
El coeficiente de restitución cr es nulo cuando Ei’ también lo es, o sea
6
cuando el sistema retiene toda la energía de deformación en su interior .
6
Generalmente en este caso los cuerpos se deforman permanentemente, aumentando su temperatura: se transforma así energía mecánica en calor, que es un tipo de
energía interna que no puede volverse totalmente a la mecánica, de acuerdo a lo que
enseña en Segundo principio de la Termodinámica.
FÍSICA – DINÁMICA Y GRAVEDAD
51
En este caso el choque es plástico o inelástico. Es el caso de una bola de
masilla que queda aplastada al estrellarse contra el suelo.
Un coeficiente de restitución unitario corresponde al caso en que la energía Ei’ restituída después del choque sea igual a la inicial Ei. Es el caso del
choque elástico. Moléculas gaseosas y otras micropartículas que por su
tamaño y naturaleza no pueden retener energía calórica, de rotación o de
vibración, interaccionan con choque elástico.
Entre estos casos límites, se encuentran los choques en los que la energía restituída
es parcial, llamados “semi-elásticos” o “semi-plásticos” , según se ubiquen hacia uno
u otro extremo del intervalo.
Ejemplo
Abandonemos por un tiempo el billar y dediquémonos a otro noble juego: las bolitas.
Tomemos una bolita de vidrio de masa m=10 g y soltémosla desde una altura h1=1 m
, Veremos que después del rebote en el piso de baldosas no recupera más que una
altura h2=80 cm .
Explicación: Una energía correspondiente a m.g.(h1-h2) = 0,20 m x 0,010 Kg x 9,8
7
2
m/s = 0,02 J queda atrapada en el sistema bolita/piso en forma de calor .
Podemos hacer el siguiente análisis dinámico y energético del fenómeno:
La energía del sistema bolita/suelo antes del choque corresponde al trabajo que
hicimos para elevar la bolita desde el suelo a un metro de altura, esto es su peso
2
multiplicado por la altura de elevación. Esa energía vale Ei = 0,01 Kg x 1 m x 9,8 m/s
= 0,1 J (es energía potencial, o sea de configuración).
La bolita llega al suelo con una fuerza viva igual a la energía potencial, o sea
2
½
½
Ei = ½ m v = , de donde v = (2.Ei/m) = (2.x0,1/0,01) = 4,47 m/s
2
El tiempo t que tarda en llegar al suelo cumple la relación h1= ½ g . t , de donde
½
½
t = (2.h1/g) = (2/9,8) = 0,45 s
Energía retenida después del choque Er= 0,02J
Energía del sistema después del choque Ei’ = Ei-Er = 0,08 J
2
Velocidad inmediatamente después del choque v’ tal que E’i = ½ m v’ , de tal manera
½
½
v’ = (2. E’i / m) = (2 x 0,08 / 0,01) = 4 m/s
Coeficiente de restitución cr= (Ei-Er)/Ei = Ei’/Ei = 0,8 (80%)
Choque elástico
7
v1
v2
v1
v
m1=m2
(m2/m1)½ .v2
De la bolita pasamos otra
vez al billar. Para simplificar el estudio despreciemos la pérdida de energía
en el choque, considerando uno elástico, de acuerdo a lo cual la energía
cinética de la bola roja en
el momento del choque
m2/m1.v2
v
m1>m2
Una delicada medición acusará un pequeño aumento de temperatura en la bolita y
en la zona del piso dónde cayó.
FÍSICA – DINÁMICA Y GRAVEDAD
52
debe ser igual a la suma de las energías cinéticas del conjunto rojo y azul inmediata8
2
2
2
mente después del choque, es decir que ½ mb v = ½ mb v1 + ½ mb v2 , o sea que
debe ser
v2 = v12 + v22 .
Esto significa que el vector v es la hipotenusa de un triángulo rectángulo de
catetos v1 y v2 . En este caso, esos catetos no están determinados, pues su
vértice común puede ser cualquiera de los puntos de una circunferencia de
diámetro igual a dicha hipotenusa y con centro en su punto medio (ver figura)
Si las bolas tuvieran masa diferente m 1 y m2, (que no es el caso del billar),
la ley de conservación del impulso nos daría:
m1.v=m 1.v1+ m2.v2 [1]
que puede escribirse
v=v1+ (m 2/m1).v2
[2]
En el dibujo de la derecha se toma en cuenta este caso, con m 1>m2
La ley de conservación de la energía aplicada al caso de masas desiguales
resulta:
½ m1.v2 = ½ m1.v12 + ½ m2.v22
[3]
que puede ponerse en la forma
v2 = v12 + [(m2/m 1)½v2]2
[4]
según está representado por la figura de la derecha.
Choque oblicuo
Ahora bien, teniendo en cuenta el principio de conservación del centro de
gravedad, equivalente al de conservación de la cantidad de movimiento,
Newton redujo el problema del choque oblicuo al del choque recto, tomando como origen de coordenadas el centro de gravedad del sistema, en
general en movimiento uniforme, o en particular en reposo. El choque recto
se puede referir al eje que une los centros de las masas (que pasa por el
centro de gravedad de ambas), transformando el fenómeno plano en unidimensional. Así, las ecuaciones vectoriales se transforman en ecuaciones
escalares, reemplazando las velocidades por sus respectivas proyecciones
sobre dicho eje.
El fenómeno del choque oblicuo para dos masas m1 y m2 que tienen las
proyecciones de sus velocidades iniciales v1 y v2 y toman velocidades
después del choque de v’1 y v’2 (también tomando sus proyecciones sobre el
eje que une las masas) está contenido en las siguientes ecuaciones escala9
res:
8
La igualdad se cumple inmediatamente después del choque, antes de que tenga
lugar la acción de las fuerzas de rozamiento de las bolas contra el paño del tapete, de
lo contrario deberá agregarse en el segundo miembro la energía correspondiente al
trabajo de dichas fuerzas.
9
Nótese que en las fórmulas siguientes no se usa la cursiva para representar las
FÍSICA – DINÁMICA Y GRAVEDAD
53
m1.v1 + m2.v2 = m1.v’ 1 + m2.v’ 2 , que también puede escribirse
m1.(v1 - v’ 1 ) + m2.(v2-v’2 ) = 0
m1 = m2.(v’ 2-v2 ) /(v1 - v’ 1 )
y además, para choque elástico es
(m 1.v12+m2.v22) = m1.v’ 12 + m2.v’ 22
[5]
La anterior se puede poner en la forma:
m1.(v12 - v’12 ) + m2.(v22-v’ 22 ) =
m1.(v1 - v’ 1 )(v1 + v’1 ) + m2.(v2-v’2 )(v2+v’2 ) = 0
[6]
De [5] y [6], resulta que debe ser
(v1 + v’1 ) = (v’2+v2 )
y por lo tanto
v1-v2=-(v’1-v’ 2)
[7]
La [3] significa que las velocidades relativas entre las masas mantienen su
valor absoluto y cambian de signo en un choque elástico.
Choque plástico
Después de un choque perfectamente plástico, es nula la energía residual
interna E’i del sistema, o sea:
2
2
Ei’ = ½ m1(v’1-v0) + ½ m2(v’2-v0) = 0
Como las masas y las velocidades al cuadrado son cantidades positivas, que la suma
de los dos términos anteriores sea nula implica:
(v’1-v0) = 0
y también
(v’2-v0) = 0
Estas dos fórmulas requieren que sea v’1 = v’2 = v0 , lo que significa que
después de un choque plástico, las masas siguen “pegadas” o fusionadas en
una sola con igual velocidad v0 que la del centro de gravedad del sistema.
Mecánica de los cuerpos rígidos
Concepto de cuerpo rígido
Los cuerpos extensos, a diferencia de las masas concentradas en partículas sin dimensión, ocupan un volumen en el espacio y por lo tanto poseen masa distribuída caracterizada por su densidad, o sea por el cociente
entre masa y volumen ocupado.
Los cuerpos sólidos extensos son en la práctica más o menos deformables por acciones externas. Se entiende por cuerpo rígido a un sólido indevelocidades, ya que éstas son proyecciones escalares de los vectores respectivos
sobre el eje que une los centros de las dos masas
FÍSICA – DINÁMICA Y GRAVEDAD
54
formable, caracterizado por su forma y por la distribución de su densidad,
que puede no ser constante (cuerpo de masa no homogénea) .
El cuerpo rígido es una concepción ideal a la que pueden asimilarse con
mucha aproximación cuerpos sólidos reales muy poco deformables.
El cuerpo rígido puede considerarse formado por una aglomeración de
gran cantidad de partículas materiales cuyas distancias relativas permanecen invariables ante cualquier acción exterior o interior. Esta concepción
“granular” responde en cierta manera a la estructura molecular de la materia.
También puede imaginarse un cuerpo rígido como formado por gran cantidad de volúmenes elementales de materia continua de densidad homogénea o no.
Llamando mi a las masas elementales y vi a los pequeños volúmenes elementales de densidad δi de los que puede considerarse formado un cuerpo,
resulta que la masa total M del cuerpo es la suma de todas las masas elementales mi , de tal manera que :
M = Σι= 01...n mi, o también M = Σ vi.δ
δ i.
mi
M = Σ mi
Pi-O
Pi
O
Centro de gravedad
Origen de referencia
Centro de masa de los cuerpos
rígidos.
En ciertas condiciones, un cuerpo rígido
puede reemplazarse por una masa de igual
valor que la su masa total, concentrada en
un punto llamado centro de masa o de
10
gravedad del cuerpo .
Como ya dijimos, el centro de gravedad es un punto de posición O tal que la
suma de las distancias (vectores) Pi-O de todos los i=1,2,3...n elementos del
cuerpo de masa m i y posición Pi cumplen la igualdad vectorial:
Σ mi.(Pi-O) = m1.(P1-O) + m2.(P2-O) + m3.(P3-O) +...+ mi.(Pi-O) +...+ mn.(Pn-O) = 0
De tal manera es, desarrollando lo anterior sale,
m1.P1 + m 2.P2 + m3.P3 +...+ mi.Pi +...+ m n.Pn= O. (m1+m2+...+m n) = O . M ,
de donde O = Σ mi.Pi / M
El vector posición O del centro de masas o baricentro de un cuerpo rígido
con respecto a un origen de referencia es igual al momento total de primer
10
Por ejemplo cuando se lo considera formando parte de un sistema con otros cuerpos separados entre sí por distancias mucho mayores que las dimensiones respectivas. Así los planetas del sistema solar podrían en ciertos análisis considerarse como
masas concentradas en sus respectivos centros de gravedad.
FÍSICA – DINÁMICA Y GRAVEDAD
55
orden Σmi.Pi del cuerpo con respecto a ese origen, dividido por la masa
total M.
Lo anterior justifica que el baricentro pueda considerarse en una primera
aproximación como el lugar representativo de la posición de un cuerpo extenso, ya que si concentráramos toda la masa allí, obtendríamos un sistema
de momento de primer orden equivalente al del cuerpo en cuestión.
Fuerza viva de los cuerpos rígidos
Consideremos un cuerpo rígido animado de un movimiento general cualquiera, que, como vimos oportunamente, puede descomponerse en una traslación y una rotación sucesivas. En base a ello, la velocidad, tomada como
cociente entre movimiento y tiempo, podrá también considerarse descompuesta en una velocidad v de traslación y otra de rotación ω alrededor de un
eje.
Se demuestra fácilmente que la fuerza viva de traslación del cuerpo rígido
de masa M como suma de las energías cinéticas individuales de mi masas a
la misma velocidad v, es equivalente a la de la masa M concentrada en su
centro de gravedad a la velocidad v , o sea Σ ½ mi v2 = ½ M v2
La fuerza viva de rotación es la suma de la fuerza viva de cada uno de los
elementos en los que podemos considerar dividido al cuerpo, de masas m i y
que están a distancias di al eje de rotación . Cada uno de ellos posee una
velocidad tangencial vti=ω
ω∧ di y fuerza viva ei = ½ mi .vti2 = ½ m i.(ω
ω∧ di)2 = ½
2
2
ω . m i.di
Momento de inercia
La fuerza viva total del cuerpo en rotación a la velocidad angular ω resulta
pués:
2
2
2
2
Σ ei = Σ ½ ω . mi.di = ½ ω [Σ
Σ mi.di ]
La sumatoria entre corchetes representa el momento de un momento, es
decir un momento de segundo orden: Como está vinculado a la energía
almacenada en cuerpos en rotación alrededor de un eje, se lo llama “momento de inercia axial”
Momento de inercia con respecto al eje X
Jx = Σ mi.di2
Para calcular el momento de inercia es necesario hacer una suma de gran
cantidad de términos a través de una operación llamada Integración, en
alguna medida contraria o inversa a la diferenciación. A continuación damos
un ejemplo, para los que conocen algo de cálculo. Los que todavía no ma-
FÍSICA – DINÁMICA Y GRAVEDAD
56
nejan las operaciones de diferenciación e integración, deben creer en el
resultado, o mejor ponerse a estudiar cálculo diferencial para juzgar por sí
mismos.
Cálculo del momento de inercia de un cilindro
de radio R y altura L con respecto a su eje
dri
ri
R
L
Lo consideraremos formado por capas cilíndricas
de igual pequeño espesor dri , cada una de ellas de
masa mi =δ
δ vi = δ.2π
π L ri dr Cada una de estas
capas elementales está a una distancia ri del eje
del cilindro, siendo entonces
J = Σ mi.ri2 = 2πδL ∫r=0
r=R
ri 3 dr = 2.π.δ.L.R4/4 =
½ π.δ.L.R4 , pero π.δ.L.R2 = M , de donde J = ½ M.R2
Las unidades en que se mide el momento de inercia son Kg/m3.m.m4 =
Kg.m2
Crónicas del CNBA
Corre una tarde de junio del año 1952. El célebre profesor Adolfo Cattáneo
prende su infaltable cigarrillo negro y lanzando bocanadas de humo, propone
a sus alumnos de tercer año nacional el siguiente....
Problema
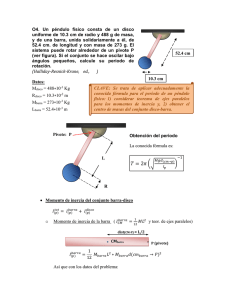
Supongamos que el alumno Rey se larga con un carrito de 4 ruedas por la barranca
de la calle Urquiza, en Vicente López, que tiene h=15 m de altura. El carrito pesa 20
Kg sin las ruedas, que son unos discos macizos de acero de R=10 cm de diámetro y
L=5 cm de espesor montados sobre cojinetes a bolilla.
El vehículo fué construido en los talleres del padre de vuestro condiscípulo Manhard
(Carlos Manhard se revuelve incómodo en su asiento, pensando en que puede ser
llamado al frente para resolver el problema)
La pregunta es: ¿A qué velocidad cruzan la bocacalle 15 m más abajo?
Despreciar pérdidas de energía por rozamiento en cojinetes, pérdidas por resistencia a
la rodadura y resistencia del aire.
Datos adicionales:
Masa del alumno Carlos Rey = 52 Kg
3
Densidad del acero δ =7900 Kg/m
4
Momento de inercia del cilindro de radio R y altura L respecto a su eje J = ½ π.δ.L.R
π.δ
Solución
- A ver Usted, mi estimado alumno Fernández, que fué el que animó a Rey a emprender este arriesgado viaje, pase y resuelva el problema – dijo A.C.
FÍSICA – DINÁMICA Y GRAVEDAD
57
Roberto Fernández Prini, desarrolla el problema diciendo:
La energía potencial del sistema carrito/ocupante de masa M se transforma al bajar
una altura h en energía cinética de traslación a velocidad v más energía de rotación de
las 4 ruedas de momento de inercia total JT = 4J que girarán a una velocidad angular
ω = v/R (suponiendo que se adhieren perfectamente al pavimento, es decir que no
patinan)
2
2
2
Así podemos poner M.g.h = ½ M v + ½ JT v /R de donde
v ( ½ M + ½ JT / R ) = M.g.h , o también v = √ 2.g.h / ( 1 + JT / M / R )
2
2
2
Masa de cada rueda: volumen por densidad : π .R .L.δ
δ = 3,14 x (0,1) x 0,05 x 7900 =
12 Kg
Masa total del vehículo más ocupante M = 4x12 + 20 + 52 = 120 Kg
3
Momento de inercia de una rueda de acero (δ
δ =7900 Kg/m ), de radio R=0,1 m y espesor L=0,05 m, con respecto a su eje de rotación.
4
2
J = π x 7900/2 x 0,05 x (0,1) = 0,062 Kg.m
Momento de inercia de las cuatro ruedas (¿Se pueden sumar los momentos de inercia? – La respuesta es SI, pero dejamos a los alumnos el porque)
2
JT = 4.J = 0,248 Kg.m
2
2
½
2 ½
Reemplazando en la fórmula anterior resulta v = (2.g.h) / (1+JT/M/R )
= √ 300 / √ (1+0,25/120/0,01) = 17,32 /1,1 = 15,76 m/s = 56,7 Km/h
=
Aquí el profesor A.C. hace notar:
- Si Rey se asusta y bloquea las ruedas con el freno, podría ocurrir que el carrito
patinara en vez de rodar. Como el tiempo está helado, puede que las ruedas se deslicen sobre la escarcha de la calle sin rodar y sin rozamiento apreciable, como en el
caso de un patín de hielo. Así no hay energía almacenada en el giro de las ruedas...
En vez de terminar a la velocidad recién calculada por Fernández,... terminará más
ligero, a la velocidad de caída libre v = √ (2.g.h) = 62,3 Km/h
-¿Qué haría para ganarle a Rey, alumno Buntinx?- Preguntó A.C.
Carlos Buntinx, contesta de inmediato:
2
2
- Fabricaría un carrito diseñado para minimizar JT/M/R = 2 π.δ.L.R
π.δ
/ M , es decir con
ruedas más livianas (de aluminio, con δ = 2500),
2500 de pequeño radio y menor espesor.
-Ajá – dijo A.C. - ¿Y no le conviene aumentar M?
- ¡Seguro!- dijo Buntinx - Lo pongo al Sr. Silvetti de piloto. (El querido “Gordo” Silvetti,
profesor de geografía, pesaba por entonces bastante más de 100 Kg)
Cuerpos rígidos sometidos a fuerzas
Vimos que un cuerpo extenso (de masa distribuida en un volumen) puede
considerarse como de estructura granular o discreta, formado por un gran
número de partículas. Este modelo coincide con la hipótesis molecular. El
grado de cohesión entre partículas determinará su estado (gaseoso, líquido
o sólido, de menor a mayor)
También puede considerarse un cuerpo extenso como de estructura conti-
FÍSICA – DINÁMICA Y GRAVEDAD
58
nua, con masa distribuída y densidad constante o variable punto a punto.
Un cuerpo extenso en el que la distancia entre puntos, elementos o partículas que lo forman permanece invariable frente a cualquier acción es un cuerpo rígido, aproximación aplicable a cuerpos reales poco compresibles y de
gran cohesión interna.
A diferencia de lo que ocurre con las partículas materiales, sobre las que
sólamente tiene sentido imaginar fuerzas aplicadas en su punto de ubicación, sobre un cuerpo extenso pueden imaginarse fuerzas ya sea concentradas en cualquier punto de su masa, ya sea distribuídas en una línea o superficie perteneciente al volumen del cuerpo.
Interesa siempre definir el lugar de aplicación de las fuerzas que pueden
actuar sobre cuerpos extensos en general y sobre cuerpos rígidos en particular, porque los efectos dependen del lugar en cuestión.
Resultante de un conjunto de fuerzas aplicadas a un cuerpo rígido
Para poder resolver los problemas en los que existen diversas fuerzas aplicadas a un cuerpo extenso, se debe tener presente que dichas fuerzas son
magnitudes vectoriales definidas por su intensidad, dirección y sentido, y
además por el punto de aplicación.
Como el cuerpo rígido es indeformable por esfuerzos internos, cualquier
fuerza aplicada puede trasladarse a lo largo de su recta de acción sin que
su efecto varíe, ya que la eventual compresión o tracción derivada del des11
plazamiento no se traduce en ninguna deformación . En cambio, aún en
cuerpos rígidos, no se puede trasladar paralelamente la recta de acción de
una fuerza sin alterar el sistema, el cual rotaría por efectos de esa traslación
lateral a menos que se compensara el efecto mediante un par de fuerzas, o
cupla, como luego se verá.
Problema general en el espacio
Fuerzas
en el
espacio
11
El estudio de cuerpos sometidos a fuerzas
en el espacio de tres dimensiones puede
reducirse en general problemas en dos
dimensiones, proyectando el sistema de
cuerpo y fuerzas sobre planos representativos. Por ejemplo, de una estructura espacial como una torre, pueden hacerse tres
estudios a través de sendas proyecciones,
Si el cuerpo es “duro” (un automóvil) da lo mismo tirar que empujar, en cambio si es
“blando” (un colchón) la tracción lo estira y la compresión lo aplasta.
FÍSICA – DINÁMICA Y GRAVEDAD
59
dos en planos verticales (ancho y profundidad) y una tercera en planta. Los
resultados se integran luego a tres dimensiones.
Problema en el plano
Por ahora consideremos un cuerpo sometido a un conjunto de fuerzas coplanares (que están todas en el mismo plano), que pueden tener cualquier
dirección y sentido, tal cual se representa en la figura. La intensidad y la
dirección de la resultante R de las cuatro fuerzas F1, F2, F3 y F4 se obtiene
sumando sus vectores representativos colocándolos uno a continuación del
otro. Sin embargo, la recta de acción sobre la que debe estar esa resultante
para que su acción sea equivalente a la de las cuatro fuerzas en conjunto, no
queda determinada con este procedimiento de suma vectorial.
Método del paralelogramo
Isaac Newton dió la pauta de cómo ubicar la resultante de dos fuerzas concurrentes en un punto a través de la regla del paralelogramo, que dice: “La
resultante es la diagonal
del paralelogramo cuyos
P
lados son las fuerzas
respectivas”. Esta regla
S
es
consecuencia
de
imaginar las acciones de
F1
f0
F1
cada fuerza repartidas en
F2
pequeños efectos que se
R12
F3
adicionan
alternativaf1
mente uno después de
F3
F
2
f2
otro, según el principio
f3
F4
Q
de superposición.
R
R34
O
f4
En la figura se ven las
resultantes parciales de
F1 y F2 en R12 , y la de F3
y F4 en R34 . Nótese que
para aplicar la regla del paralelogramo es necesario llevar a concurrencia en
un punto cada fuerza del par mediante sendas traslaciones de sus puntos de
aplicación sobre las respectivas rectas de acción.
Polígono Funicular
R
F4
Sumadas a su vez las resultantes parciales R12 y R34 aplicando la regla del
paralelogramo, se obtiene la resultante total R aplicada en el punto P. El
hecho de que P esté fuera del cuerpo no tiene importancia por tratarse de un
cuerpo rígido, en el que es equivalente aplicar la fuerza en cualquier punto
de su recta de acción PQ (por ejemplo en S)
Método del polígono funicular
En la figura se ve además otro procedimiento para obtener la resultante de
un sistema de fuerzas coplanares que pueden ser concurrentes o no, es
FÍSICA – DINÁMICA Y GRAVEDAD
60
decir que algunas o todas pueden ser paralelas entre sí. No es éste el caso
del método del paralelogramo, sólo aplicable al caso de fuerzas no paralelas
en el plano, esto es concurrentes en un punto.
El método, llamado del “polígono funicular” por lo que explicaremos luego,
consiste en trabajar sobre el polígono de fuerzas, eligiendo un punto O (llamado polo) desde el que se trazan rectas hasta los extremos de los vectores
representativos de las fuerzas aplicadas al cuerpo rígido. Quedan así formados una serie de triángulos cuyos lados con vértice en O representan dos
componentes cuya suma es el vector representado por el tercer lado. Por
ejemplo F1 queda descompuesta en las componentes f0 y f1. La fuerza F2
queda descompuesta en –f1 (ojo al signo) y f2. De tal manera F2=f2-f1. Y así
sucesivamente hasta llegar a la última fuerza, en este caso F4, descompuesta en –f3 y f4. Resulta claro que f0 + f4 es la resultante R del sistema
Conociendo su dirección y la de las cinco fuerzas auxiliares f0, f1, f2, f3 y f4
por medio de la construcción anterior, se hace corresponder al polígono de
fuerzas una línea quebrada (poligonal) cuyos lados son respectivamente
paralelos a las fuerzas auxiliares. Esta poligonal se traza sobre las rectas de
acción de las fuerzas en el plano. La prolongación del primero y último lado
de la misma se cortan en un punto Q de la recta de acción de la resultante.
ESQUEMA DE UN DINAMÓMETRO DE RESORTE
Justificación del método del polígono funicular
Dinamómetro
Un resorte alojado en un tubo, con un
estilo solidario que pueda marcar su alargamiento sobre un escala lineal es
un instrumento apto para medir fuerzas. Es un dinamómetro de resorte. Se lo
gradúa en Newton o en Kg, colgándole pesos conocidos.
F
F
10
9
8
7
6
5
4
3
1
0
Newton
Experiencia:
Con varios de estos instrumentos y un hilo resistente se puede armar un
conjunto como el de la figura.
Allí se ve que el hilo adopta
F1
A
la forma del polígono funicuf0
F2
B
f1
lar. Precisamente, funicular
f2 R
deriva del latín funiculum:
F
3
O
f0
cuerda o cable. Es que un
f3
cable o cuerda se tensa por
F4
f4
f4
la fuerza a la que está somef1
f2
tido, indicando por lo tanto su
F1
f3
dirección.
F4
F2
Si los dinamómetros están
bien calibrados, marcarán
fuerzas proporcionales a los
vectores dibujados en el
F3
R
FÍSICA – DINÁMICA Y GRAVEDAD
61
polígono de fuerzas. Moviendo los puntos A y B de amarre del hilo al cuerpo,
cambiarán las direcciones de f0 y f4 y el polígono funicular se corresponderá
con un dibujo con el polo O en otro lugar.
Momento de una fuerza con respecto a un punto
Se llama momento de una fuerza F con respecto a un punto O del espacio,
al producto vectorial M = F∧
∧ d entre el vector representativo de la fuerza y
el de la distancia entre el punto de aplicación de la misma y el punto de referencia d = OF-O , punto que no tiene necesariamente que pertenecer al
cuerpo sobre el que la fuerza está aplicada. El momento de una fuerza es
una entidad creada y usada para representar el efecto de la fuerza sobre un
punto del cuerpo. En el párrafo siguiente se verá su importancia al considerar la traslación de la recta de acción de una fuerza. El momento de una
fuerza depende, de acuerdo a su definición, de la fuerza y la distancia al
punto de referencia. Averiguar el momento de una fuerza con respecto a un
punto (tomar momentos, como se dice en la jerga de los especialistas) supone considerar el efecto de esa fuerza sobre el cuerpo en la que está aplicada
como si éste tuviera libertad de movimiento alrededor de aquél.
Casos en que el momento de una fuerza con respecto a un punto es
nulo
M|
sen (F^d)
(F^d)
Es importante tener en cuenta cuándo es nulo |M|=F.d.
.
el momento, porque indica alguna de las conF
diciones siguientes:
M
•
El momento de una fuerza con respecto a
d
cualquiera de los puntos de su recta de
acción es nulo. Esta propiedad es eviO
dente, ya que en ese caso el factor disd’ = d. sen(F^d)
tancia d es nulo.
M
OMENTO
DE
UNA
FUERZA
F CON RESPECTO
•
También es nulo el momento cuando la
PUNTO O
resultante es nula (o sea el otro factor del AL
.
producto vectorial). No tiene sentido estudiar el caso de que ambos sean nulos, ya que si no hay resultante, no puede plantearse la distancia
de su recta de acción
•
De acuerdo a lo que sabemos de producto vectorial, podría ser nulo
cuando los vectores son paralelos. Se ve en la figura que los vectores d
y F están “enganchados” uno a continuación del otro. Así que la única
manera de que sean paralelos es que coincidan sus rectas de acción, lo
que reduce este caso al primero.
Momento y Trabajo
El momento es una magnitud vectorial, cuya unidad es fuerza por distancia.
Por definición de producto vectorial su módulo resulta
^
^
|M
M | = | F ∧ d | = F.d sen (F d) = F.d’ , para d’ = d.sen (F d) , que es la distancia de la recta de acción de la fuerza al punto O, con respecto al cual se
FÍSICA – DINÁMICA Y GRAVEDAD
62
considera el momento
El momento de una fuerza no debe confundirse con trabajo T de una fuerza,
^
que como ya viéramos es un escalar definido por T = F.d = F.d cos (F d)
Trabajo tiene unidades de energía, y es sólo parecido desde el punto de
vista dimensional al momento. La distancia en aquél es el camino recorrido
por la fuerza, mientras que en el caso del momento es la distancia fija al
punto de referencia.
Momento de un sistema de fuerzas
Por ser el momento una cantidad vectorial, el momento total de un sistema
de fuerzas es la suma de los momentos de cada una de las fuerzas con
respecto al punto considerado. Si tenemos en cuenta que la resultante R de
un sistema debe ser equivalente a todas las fuerzas, su momento M R con
respecto a cualquier punto debe ser igual a la suma de momentos de cada
una, o sea al momento total. Es decir:
M i = Fi ∧ di
Momento de una fuerza Fi
Momento de todas las fuerzas
M T= Σ M i = Σ Fi ∧ di
Momento de la resultante
M R = M T = Σ Fi ∧ di = R.∧dR
La distancia vectorial dR representa la posición o punto de aplicación de la
resultante R, y como ésta es la suma de las fuerzas R = Σ Fi , de la tercera
ecuación sale:
Σ Fi ∧ di
= (Σ Fi ) ∧ dR
La igualdad anterior puede escribirse tomando módulos de los vectores en
ambos miembros. Se debe recordar que los momentos de fuerzas coplanares son paralelos, ya que todos son perpendiculares al plano, por lo que el
módulo de su resultante es la suma de los módulos de cada uno de los momentos.
Además téngase presente que la distancia de la recta de acción de la fuerza
^
al punto considerado vale d’=d.sen(F d) (ver figura de la página anterior)
Así resulta que
|Σ
Σ Fi ∧ di | = |(Σ Fi ) ∧ dR | y también
Σ Fi .d’i = d’R . Σ Fi
de donde d’R = Σ Fi .d’i / | Σ Fi |
Es decir que la distancia de la recta de acción de la resultante al punto con-
FÍSICA – DINÁMICA Y GRAVEDAD
63
siderado es igual al momento de primer orden de todas las fuerzas dividido
la resultante de todas ellas. Por supuesto que si el punto desde el cual se
toman momentos pertenece a la recta de acción de la resultante es d’R =
Σ Fi .d’i =0
Traslación de la recta de acción de una fuerza - Cupla
Vimos que el punto de aplicación de una fuerza sobre un cuerpo rígido puede trasladarse a lo largo de su recta de acción sin que su efecto varíe. En
cambio el desplazamiento paralelo d de una fuerza F fuera de su recta de
acción cuando está aplicada sobre un cuerpo cualquiera, aunque sea rígido,
no puede hacerse sin que cambie el efecto que inicialmente tenía sobre éste.
Para entender el efecto de esa traslación, pueden considerarse aplicadas en
el punto donde se quiere trasladar, dos fuerzas iguales y contrarias cada una
del mismo valor a la considerada, que lógicamente tienen resultante nula.
Este cambio, que no afecta al
-F
sistema siempre que se trate de
A
un cuerpo rígido, nos permite ver
A
que la traslación de una fuerza
B
F
B
requiere la aplicación adicional de
F
F
un par de fuerzas de igual magnitud y sentido contrario cuyas
rectas de acción están precisad
mente a una distancia igual al
desplazamiento d considerado.
Momento de una cupla
Un cuerpo rígido con una fuerza F aplicada en el punto A
Un par de fuerzas o cupla puede es equivalente al mismo cuerpo con esa fuerza F
caracterizarse por una magnitud trasladada al punto B más un par de fuerzas o cupla de
∧d
F –F cuyo momento vale M = F∧
igual al producto vectorial de la traslación
fuerza por la distancia, es decir M = F∧
∧ d . Esta magnitud coincide con la
suma de los momentos de primer orden de las dos fuerzas del par, tomadas
con respecto a cualquier punto O del espacio, perteneciente o no al cuerpo.
M =F.d1-F.d 2=F(d1-d2)=F.d
O
d2
F
d2
M =F∧
∧d
d1
d1
d
-F
En la figura adjunta no se ha representado el vector momento M , que de acuerdo a la convención usada en esta obra
para el producto vectorial, debería ser
uno perpendicular al plano del dibujo. En
cambio se ha indicado mediante una
flecha curva el efecto de rotación que el
par de fuerzas produciría en el cuerpo si
se dejara librado a su acción. La fórmula
escalar anotada en la figura |M
M | =F.d es
válida además de la expresión vectorial,
FÍSICA – DINÁMICA Y GRAVEDAD
64
al ser en este caso particular los factores perpendiculares entre si.
De lo anterior surge claramente que el momento de una cupla es igual en
todos los puntos del plano. En cambio el momento de una fuerza varía con
respecto al punto desde el cual se toma.
Cuando un conjunto de fuerzas coplanares presenta un momento M invariable con respecto a cualquier punto, es porque no es reducible a una sola
fuerza resultante. En cambio es equivalente a un par de ellas opuestas,
iguales y paralelas, es decir una cupla, cuyo momento vale M
Desde el punto de vista práctico, una fuerza muy pequeña (despreciable)
con respecto a un punto muy alejado representa aproximadamente una cupla, ya que su resultante es aproximadamente nula mientras que su mo12
mento no lo es.
Composición de fuerzas paralelas aplicadas al cuerpo rígido
Con el método del polígono funicular, visto antes, se puede hallar la resultante cualquiera sea la disposición de las fuerzas en el plano y por lo tanto
también para fuerzas paralelas.
En este caso particular, como la resultante es equivalente a todas las fuerzas
aplicadas una a continuación de la otra a lo largo de la recta de acción, si
trasladamos paralelamente cada una de las fuerzas sobre dicha recta (puntos gruesos en la figura), deben anularse todos los momentos correspondientes a cada traslación. Esta condición es necesaria para obtener un sistema equivalente al primitivo,
d
d
sin momento M . Refiriéndonos
d
a la figura, lo anterior se resume en la siguiente ecuación
R
vectorial:
1
2
3
Σ Fi ∧ di= 0
F
[1]
F
F
F
F
Donde los vectores d son las
R
distancias correspondientes de
d
d
cada fuerza al punto de aplicaComposición de fuerzas paralelas
ción de la resultante. Dado que
las fuerzas son paralelas, la
anterior se puede reemplazar por la ecuación escalar:
1
4
2
5
3
4
5
12
El producto de una cantidad infinitamente pequeña por otra infinitamente grande no
es nulo ni infinito: toma un valor que depende de cómo tienden a cero e infinito respectivamente sus factores.
FÍSICA – DINÁMICA Y GRAVEDAD
65
ΣFi.di= 0
[1 bis]
en la que los signos de las distancias escalares d entre recta de acción de la
fuerza y la resultante, son positivos o negativos según se midan hacia la
derecha o hacia la izquierda de la fuerza. También puede considerarse que
Fi.di es positivo o negativo según tienda a hacer girar el sistema en contra o
a favor del reloj. Así, en la figura F5.d5 es positivo, mientras que F1.d1 es
negativo
Por otra parte, el valor de la resultante R debe ser igual a la suma vectorial
de todas las fuerzas, es decir:
Σ Fi = F1+F2+F3+F4+F5 = R
[2]
Por ser fuerzas paralelas, la anterior se reduce a la igualdad escalar:
Σ Fi = F1+F2+F3+F4+F5 = R
[2 bis]
La [1 bis] y la [2 bis] significan que se puede reemplazar un conjunto de
fuerzas paralelas que actúen sobre un cuerpo rígido, con una resultante cuya
intensidad sea igual a la suma aritmética de las intensidades de todas las
fuerzas, colocada sobre una recta paralela con respecto a la cual será nulo
el momento de primer orden Σ Fl .dl
Fuerzas concentradas y distribuídas
Hasta ahora hemos considerado fuerzas aplicadas
en un punto de un cuerpo rígido, pensando en una
fuerza concentrada sobre una partícula material.
Por más que las acciones sobre cuerpos extensos
se pueden pensar como fuerzas concentradas
sobre ciertas partículas constitutivas del mismo,
también es útil considerar a veces otro modelo en
el que las acciones se representan por fuerzas
distribuídas en una zona extensa (línea o superficie) del cuerpo. Por ejemplo, en primera aproximación el peso del programador sobre el asiento puede considerarse que se ejerce a través de una PRESIÓN DEL PROGRAMADOR SOBRE
fuerza concentrada en el medio de la tabla del EL ASIENTO Y SOBRE EL PISO
banco. Es más ajustado pensar en dos fuerzas paralelas en cada glúteo, o
mejor aún una presión distribuída sobre la superficie de contacto del cuerpo
sobre el asiento y los pies en el suelo. En el dibujo, las zonas más oscuras
corresponden a mayor presión.
La presión del viento sobre un cartel publicitario, la fuerza de la explosión en
un cilindro de un motor sobre el pistón y aún el peso de el cuerpo sobre un
patín de hielo se representan mejor con fuerzas distribuídas sobre las superficies o líneas en las que actúan.
FÍSICA – DINÁMICA Y GRAVEDAD
66
Esta mejor aproximación, no indispensable en cuerpos rígidos, es de rigor
cuando se consideran los efectos de las acciones sobre cuerpos deformables, ya que en éstos la presión produce una deformación local proporcional
a la misma, como veremos al tratar la mecánica de los cuerpos sólidos elásticos.
El concepto de fuerza, masa o en general cualquier magnitud distribuída en
un cuerpo, se entiende pensando primeramente en la magnitud concentrada
en un punto representativo de todo el cuerpo, y luego considerando al cuerpo formado por un conglomerado de pequeñas partículas a las que se aplica
el mismo criterio. Llevando al límite ese proceso mental, se puede llegar a
pensar que la magnitud concentrada es tan chica que lo que interesa es el
cociente entre el valor pequeñísimo de esa magnitud y el valor también minúsculo de la región del cuerpo a la que pertenece. Por ejemplo, la densidad
en un punto de un cuerpo es el límite del cociente entre la masa y el volumen
cuando consideramos a éste infinitamente pequeño en una región que contiene al punto considerado.
Una presión resulta igualmente de considerar el cociente entre fuerza y superficie, cuando ésta tiende a cero. La fuerza por unidad de longitud que
ejerce el filo de un patín sobre el hielo es igual al peso del patinador divido la
longitud de la arista del patín.
Densidad, presión y peso por unidad de longitud son magnitudes distribuídas
aplicables cuando se considera a la materia formada por una sustancia continua, sin granos o discontinuidades. Cuando se adopta el modelo de cuerpo
continuo, la fuerza concentrada es una aproximación para representar una
gran presión ejercida en una superficie muy pequeña, como la que ejercen
las finas patas del banco donde está sentado el programador.
La adopción de modelos distribuídos o concentrados está en general aconsejada por la escala o
grado de detalle que pretendemos dar a la descripción y estudio de los fenómenos. Por ejemplo. una
cadena colgada de los extremos puede estudiarse
como tal, con eslabones independientes sobre los
que actúa un peso concentrado, o como una cuerda o cable de masa distri13
buída en una línea: la elección depende de la cantidad de eslabones .
13
Una cuerda o hilo puede considerarse a su vez como una cadena de infinidad de
pequeños eslabones de fibras entrelazadas.
FÍSICA – DINÁMICA Y GRAVEDAD
67
Gravedad
Hemos visto que la variación de la cantidad de movimiento de los cuerpos se
asigna a la acción de fuerzas, aplicadas por contacto con otro cuerpo, como
en el caso del choque, o por empuje o tracción desde otro sistema a través
de un vínculo (la mano que empuja un objeto, el cable que tira del ascensor,
etc.). Sin embargo, la fuerza más común que es el peso que experimentan
los cuerpos, esa fuerza que los impulsa a caer contra la tierra, se ejerce sin
la intervención de un vínculo o medio material intermedio entre objeto y tierra. Es una acción a distancia, aparentemente ejercida desde la tierra sobre
toda la materia. Se la llama fuerza de gravedad.
La gravedad o atracción gravitatoria se puede estudiar en escala terrestre
como la fuerza que aparece sobre todos los objetos, dirigida verticalmente
hacia abajo y que es proporcional a la masa a través de una constante que
tiene lógicamente dimensiones de aceleración. Es la “aceleración de la gravedad”, representada por la letra g. La experiencia demuestra que g varía
con la altura y con la posición en el planeta: no vale lo mismo en Buenos
Aires que en Sucre. No vale lo mismo en los polos que en el ecuador, ni en
la cima del Aconcagua que a nivel del mar. Pronto veremos por qué.
Sin embargo, esas variaciones son prácticamente muy pequeñas a escala
terrestre, y en todas las aplicaciones será una aproximación suficiente tomar
a g = 9,8 m/s2 e incluso a veces redondear g = 10 m/s2
Peso
Así, sobre un cuerpo de masa m está aplicada una fuerza, llamada peso,
igual a P = m.g
Si esa fuerza no se equilibra con una reacción contraria de algún objeto o
vínculo unido a tierra (columna, soporte, viga, etc.) el cuerpo cae con una
aceleración igual a P/m = g , llamada por eso “aceleración de la gravedad”
Por efectos del peso, los cuerpos caen con movimiento acelerado exclusivamente de traslación, verticalmente hacia abajo. El peso puede ser considerado como resultante de fuerzas paralelas elementales proporcionales a
su densidad aplicadas en cada porción o partícula constitutiva del cuerpo, o
lo que es equivalente en el caso de cuerpos rígidos, una única fuerza proporcional a la masa total del cuerpo aplicada en un punto de la resultante de
esas fuerzas paralelas, llamado “centro de masas, centro de gravedad o
baricentro”
FÍSICA – DINÁMICA Y GRAVEDAD
68
Centro de gravedad
Llamado también centro de masas o baricentro, el centro de gravedad es
el punto donde puede considerarse aplicado el peso de un cuerpo rígido
para obtener una acción equivalente a la de la gravedad, o la masa para
14
obtener una acción equivalente a la fuerza de inercia.
Se determina fácilmente el centro de gravedad de un cuerpo rígido suspendiéndolo de dos puntos diferentes: Las verticales trazadas desde los puntos
de suspensión se cortan en el centro de gravedad.
O
DETERMINACIÓN DEL
CENTRO DE GRAVEDAD
O BARICENTRO
En efecto, cuando se suspende un cuerpo con libertad
de rotación alrededor de un punto, la fuerza necesaria
para sostenerlo forma con el peso una cupla hasta que
las dos rectas de acción coinciden en la vertical. Repitiendo el procedimiento desde otro punto, la nueva
vertical corta a la primera en el centro de masas o baricentro. En el dibujo se ve un cuerpo de dos dimensiones (una chapa) cuyo centro de masas está afuera del
propio cuerpo.
La determinación del centro de gravedad se puede resolver geométricamente si el cuerpo en cuestión tiene densidad constante en todo su volumen.
En tal caso, cada volumen elemental en que puede ser descompuesto tendrá
un peso proporcional a su extensión. Por ejemplo, el centro de gravedad de
un arco de alambre homogéneo, se puede encontrar dividiéndolo en pequeños
arcos iguales. Considerando que dos de
ellos tienen un centro de gravedad situado en el punto medio de la recta que los
une, se reemplaza el cuerpo por otro
formado por la mitad de los elementos
originales colocados en los centros de CENTROS DE MASAS DE ALAMBRES HOMOGÉNEOS
gravedad de cada par. Así sucesivamente, se tiende a un único punto, que
es el centro buscado.
Ley de la gravedad
Se dice que Sir Isaac Newton se inspiró en la caída de una manzana para
plantear su famosa ley de gravitación. Es bien probable que así sea. Newton
fué capaz de intuir que la caída de una manzana con el fondo de la luna
llena que se pone en el horizonte matutino, representan dos efectos de una
14
Un cuerpo deformable tiene un centro de masas que cambia de posición en cuanto
se lo somete a esfuerzos.
FÍSICA – DINÁMICA Y GRAVEDAD
69
misma causa. Manzana y luna caen atraídas por la tierra con velocidades
paralelas. La primera choca con el suelo y la segunda no lo hace pués su
trayectoria no corta a la superficie terrestre. Si pudiéramos lanzar la manzana con fuerza prodigiosa “afuera” de la tierra, caería como la luna, más allá
del horizonte.
La trayectoria cerrada u órbita de la luna
alrededor de la tierra indica que existe un
movimiento central (ver página 22), con
aceleración dirigida hacia la tierra. La magnitud de esa aceleración se deduce de la
trayectoria aproximadamente circular que
describe nuestro satélite, de velocidad
angular ω = 2π
π/T con
15
T = 27,3 días = 2,36x106 s , de donde
-6
ω = 2,66x10 rad/s
El hecho de que la órbita sea estable, o
Isaac Newton en la
quinta de Lincolnshire,
sea que la luna no escape o se precipite
observando la caída de
sobre nosotros, indica que existe una fuerla manzana
za de atracción igual a la masa de la luna
multiplicada por la aceleración centrífuga del movimiento. Por lo ya estudiado sabemos que la aceleración centrífuga vale ac = ω2.R , con R = 384x106
m (radio de la órbita de la luna), de donde ac = 2,72 x 10–3 m/s2
Este valor es la aceleración de la gravedad a la distancia que se encuentra la
luna, o sea a 384000 Km. Es evidente que la aceleración disminuye con la
distancia a la tierra, ya que aquí vale 9,8 y allá vale g/ac = 3596 veces menos.
Para averiguar la relación entre gravedad y distancia, Newton comparó
este número con la relación entre distancias respectivas. La aceleración g =
9,8 m/s2 se experimenta sobre la tierra, a una distancia igual al radio de
nuestro planeta (6400 Km), tomada desde el origen del movimiento central, o
sea desde el centro de gravedad de la tierra. En la luna, a 384000 Km de
distancia (60 veces más) la gravedad es 3600 veces menor. La relación
entre 60 y 3600 es clara: el segundo es el cuadrado del primero. Por lo
tanto, la fuerza de gravedad disminuye con el cuadrado de la distancia.
En general, a la distancia d del centro de la tierra (de radio R), la gravedad
2 2
vale g.R /d
15
Como se sabe, la luna completa su ciclo en aproximadamente cuatro semanas,
tiempo en el que da una vuelta completa a la tierra.
FÍSICA – DINÁMICA Y GRAVEDAD
70
La fuerza sobre un cuerpo de masa m situado allí, valdrá F = m.g.R2/d2
Por el principio de acción y reacción, la fuerza que ejerce el cuerpo de
masa m sobre la tierra valdrá igualmente F , igual al producto de la masa de
la tierra M por la aceleración creada por el cuerpo de masa m, gravedad
superficial g’ y radio r , de manera que F = M.g’.r2/d2
Comparando ambas fórmulas resulta que M g’ r2 = m.g.R2 , de donde
g.R2/M = g’.r2/m
Esta relación entre gravedad superficial multiplicada por radio del cuerpo al
16
cuadrado y dividido su masa es una constante independiente del cuerpo,
llamada constante de gravitación universal kG. Reemplazando los valores
para la tierra, de masa
M = 5,98 10 24 Kg y radio R = 6400000 m resulta
kG = 9,81 m/s2 . 64000002 m2/ 5,98.10 24 Kg = 6,72.10-11 m3/Kg/s2
Multiplicando y dividiendo por m la fórmula F = M.g’.r2/d queda
F = M m. (g’.r2/m) / d2 = kG M.m/d2
En base a la fórmula anterior Newton enunció la ley de gravitación afirmando
que “todo pasa como si los cuerpos se atrajeran con una fuerza proporcional
al producto de sus masas e inversamente proporcional al cuadrado de la
distancia que los separa”
Gravedad en la superficie de un cuerpo
Para cuerpos esféricos de radio r y densidad constante δ resulta que su
masa vale
m = 4/3 π r3 δ , de donde kG = g’ r2/m = g’/(4/3 π r δ) = g’ 3/4/π
π /(r.δ
δ ) = 0,2387
g’/(r δ)
Se deduce de la anterior que la gravedad superficial g’ es proporcional a la
densidad y al radio del cuerpo.
17
Si la tierra fuera una esfera de radio R = 6378 Km y densidad constante
igual a su masa dividida el volumen, resultaría:
δ = M/(4/3 π R3) = 5.98.1024 kg / 1,09.1021 m3 = 5502 Kg/m3
16
Se supone un cuerpo esférico. Para una forma cualquiera habrá que usar el radio
de la esfera de igual material e igual peso.
17
La tierra no es una esfera perfecta: es ligeramente achatada en los polos. Tampoco
tiene densidad constante ni es homogénea: su núcleo es más denso que la corteza y
superficialmente mares y continentes tienen diferente densidad.
FÍSICA – DINÁMICA Y GRAVEDAD
71
y para iguales dimensiones y peso, debería tener una gravedad superficial
de
g = 4.π/3.kG.R.d = 9,808 m/s2
Alcance de la ley de gravitación
Vimos que en base a consideraciones astronómicas, Newton dedujo hace
trescientos años la ley F = M m. (g’.r2/m) / d2 = kG M.m/d2, que expresa la
fuerza de atracción que existe entre dos cuerpos de masa M y m separados
por la distancia d
¿A qué distancia se refiere la fórmula?. En su deducción se tuvieron en
cuenta masas muy alejadas (tierra y luna) comparadas con sus dimensiones.
Esa relación pequeña entre tamaño y distancia (R/d=6400/384=1/60) hace
poco relevante la forma de tomarla (entre centros de gravedad o entre zonas
más próximas de los cuerpos). La idea es que la ley es aplicable a masas
concentradas en pequeñas dimensiones comparadas con las distancias que
las separan. Se demuestra que si las masas no son esféricas y homogéneas, y tienen una extensión importante respecto a la distancia que las separa, el efecto gravitatorio existe, pero la fórmula no es aplicable en forma
estricta.
En teoría se puede plantear el problema dividiendo a los cuerpos en pequeñas porciones y considerando la suma de las interacciones gravitatorias
entre estas pequeñas masas elementales separadas por distancias comparativamente grandes. Este método fué desarrollado por Isaac Newton por
medio de un procedimiento que dió origen al moderno cálculo infinitesimal.
Fuerzas a distancia – Campo y potencial gravitatorio
Las acciones gravitatorias se estudian con ventajas a partir de la teoría del
campo y potencial, ya esbozada en la parte de esta obra que trata de la
energía potencial, y que ahora ampliaremos.
La gravedad, las fuerzas entre cuerpos electrizados y las atracciones y repulsiones magnéticas son las manifestaciones más comunes de fuerzas a
distancia, es decir esas acciones que se manifiestan sin la intervención de
un medio material que sirva para “empujar” o “tirar” de los cuerpos.
Sin la intención de explicar el porqué de estos efectos a distancia, sino más
bien con la idea de describir el “cómo” de la ocurrencia de estos fenómenos,
es que se imagina a las masas en el caso de la gravitación, a los cuerpos
cargados o recorridos por corrientes eléctricas en el caso de las fuerzas
electrostáticas y magnéticas, como fuentes o sumideros de un fluído incorpó-
FÍSICA – DINÁMICA Y GRAVEDAD
72
reo llamado “campo”.
Campo gravitatorio
Mientras el campo eléctrico parece salir de las cargas positivas y sumirse en
las negativas y el campo magnético se parece a un fluído arremolinado en
un vórtice, donde circula la corriente eléctrica que lo produce, el campo gravitatorio funciona como un fluído que entra en las masas y cuya fuente es el
propio universo que las rodea.
Esta concepción o modelo está autorizado por la ley de la inversa del cuadrado de la distancia, que es la misma que gobierna el flujo de agua que
18
entra en un desagüe colocado en el interior de una pileta muy grande.
Supongamos en un punto dentro de una masa de
agua se instala la boca de un caño que absorbe
un flujo o “gasto” G Kg/s . Admitamos que la boca
v
está construida para que el agua entre por igual
r
en todas direcciones. Una esfera imaginaria de
radio r con centro en la boca de salida, será atravesada en toda su superficie por el flujo constante
G (m3 /s)
G, de manera que la cantidad de agua por unidad
de superficie y por unidad de tiempo a través de la
esfera de radio r y superficie S = 4π r2 valdrá:
G/S = G/(4.π.r2) [Kg/s/m2]. A esta cantidad G/S la llamaremos flujo específico
o gasto específico. Como se ve en la fórmula, el flujo específico G/S es inversamente proporcional al cuadrado de la distancia a la fuente (la boca de
salida del caño).
La relación entre flujo específico, densidad δ y
velocidad v del fluído en un punto es :
G/(4.π.r2) = δ [Κg/m3].v [m/s]
Los vectores v en la masa fluída se distribuyen
marcando direcciones de “líneas de corriente”,
que son las trayectorias que siguen las partículas del fluído. Las líneas de corriente entran radialmente si los sumideros son
puntuales y siempre perpendicularmente a las superficies cuando los sumideros son extensos. Si el caño de salida tiene una hendidura en vez de una
boca distribuidora esférica, entrarán las líneas de corriente a lo largo de esa
hendidura. Si es un plano permeable, entrarán líneas perpendicularmente a
ese plano, como se muestra en la figura.
SUMIDERO PLANO
18
También es válido para un fluído que sale. Lo único que cambia es la dirección de
la velocidad. El modelo para electrostática considera como fuente a las cargas positivas y sumideros a las negativas.
FÍSICA – DINÁMICA Y GRAVEDAD
73
La analogía fluída nos permite afirmar que en una masa M entra un fluído
gravitatorio con una intensidad J = kG..M/r2 tal que produce sobre otra masa
m una fuerza F=J.m cuya dirección es el de las líneas de corriente.
Llamaremos a J “campo gravitatorio”. J tiene dimensiones de aceleración, y
coincide con g cuando M =masa de la tierra y r = radio de la tierra.
Teorema de Gauss
Aplicado a la gravitación, el teorema dice que la cantidad de fluído gravitatorio que pasa hacia adentro por una superficie cerrada (por ejemplo una esfera) que contiene a las masas donde se sume, es proporcional a las mismas y
vale J.4.π
π.r2 = 4.π
π. kG..m , de donde J.r2 =kG..m .
Significa lo anterior que el flujo de gravedad que pasa por una superficie
cerrada es proporcional a la masa total encerrada por esa superficie.
Reconociendo estos principios de analogía podemos afirmar que no hay
19
campo gravitatorio dentro de una cáscara material cerrada , ya que adentro
no hay fuentes que puedan proveer el fluído necesario para sumirse en la
cáscara material. En cambio, afuera de la misma existe un mar de fluído
ilimitado que puede proveerlo para que entre en la cáscara perpendicularmente a la superficie, como si las líneas de corriente se dirigieran al centro
de la esfera.
Representándose una esfera homogénea como formada por una sucesión
de capas finas superpuestas (como en una cebolla), apoyándose en la consideración anteriormente expuesta es válido reemplazar cada capa por una
masa equivalente en el centro. Repitiendo el proceso para todas ellas, queda
reemplazada una esfera homogénea por una suma de masas puntuales
igual a la masa total concentrada en su centro.
Queda así perfectamente justificada la suposición de Newton de que la fuerza gravitatoria de la tierra sobre la manzana era equivalente a la acción de
una masa M en el centro de la tierra, es decir a la distancia R (radio de la
tierra) de la manzana.
Gravedad en acción
La gravedad tiene dos acciones principales que se observan permanentemente: la caída de los cuerpos y el peso de los objetos.
19
Newton demostró mediante el cálculus, que cada porción de la cáscara provoca una
acción gravitatoria en su interior que está compensada por otra zona opuesta, de
manera que la resultante es nula.
FÍSICA – DINÁMICA Y GRAVEDAD
74
Caída de los cuerpos – Masa inercial y gravitatoria
Galileo y Newton observaron que los cuerpos pesados caen todos con la
misma aceleración si evitamos la resistencia del aire. En un tubo sin aire
monedas y plumas caen juntos, con aceleración constante igual a 9,8 m/s2.
Esa constante vale, de acuerdo a la ley de gravitación universal g=kGMT/R2
(MT = masa de la tierra; R = radio de la tierra). Multiplicada g por la masa de
un objeto m nos da la fuerza de gravitación sobre la superficie terrestre, a la
distancia R del centro de la tierra. Esa fuerza se llama peso del cuerpo, proporcional a su masa.
El principio de inercia dice que toda acción que tienda a modificar el estado
de reposo o de movimiento uniforme de un cuerpo, produce una reacción
igual y contraria proporcional a su masa y a esa acción perturbadora.
La masa gobierna, pués, tanto la atracción gravitatoria como la fuerza de
inercia. Tiene sentido pensar que ambos efectos deban tener un origen común, o visto desde otro ángulo, que la igualdad entre la masa de un objeto
deducida de su inercia o de su peso sugiere una conexión entre la aceleración a y el campo gravitatorio g
Ernst Mach, notable físico y filósofo alemán del siglo pasado, aventuró la
idea de que la inercia era efecto de la masa de todo el universo, que se resistía a que un objeto se acelerara con respecto a todo ese resto de la materia. Desde este punto de vista, un objeto solitario en todo el universo no
presentaría inercia, como que no tendría sentido hablar de su posición, velocidad y aceleración, que requieren algún punto de referencia. Tampoco estaría sujeto a fuerzas de gravitación de otros cuerpos, por otra parte inexistentes.
Saliendo de estas disquisiciones metafísicas, nos encontramos en realidad
con el hecho de que la masa es una propiedad de la materia que gobierna la
gravitación y la dinámica, y puede manifestarse ya sea como acción gravitatoria recíproca con otro cuerpo o como resistencia al cambio con respecto a
un sistema de referencia inercial.
Péndulo
Cualquier objeto rígido de masa m y peso P=m.g , suspendido en un punto
O por encima de su centro de masa G y sometido a la gravedad g es un
péndulo físico. En su posición de equilibrio un péndulo se mantiene de
manera que el punto de suspensión O y su centro de gravedad G pertenecen
a la recta de acción de la fuerza a que está sometido. Si ésta es la gravedad,
la fuerza es el peso P = m.g y ese eje será vertical.
Apartado de su posición de equilibrio en un ángulo αmáx y abandonado, un
péndulo oscila, esto es, se mueve alrededor del punto de suspensión O
FÍSICA – DINÁMICA Y GRAVEDAD
75
rotando hacia un lado y hacia el otro de su posición de equilibrio, realizando
una ida y vuelta completa en un tiempo siempre igual T, llamado período de
oscilación. La causa de esas oscilaciones es la transferencia de energía
potencial máxima cuando está quieto en los puntos extremos, a cinética
máxima cuando su eje es vertical.
-P
-P
O
La amplitud de esa oscilación, medida
por el ángulo αmáx, va disminuyendo poco
a poco debido a fuerzas de rozamiento en
su punto de suspensión O y a la resistencia del aire sobre la superficie del cuerpo.
-P
O
O
G
P
EJE del péndulo
l
G
G
l.sen(αα)
P
II
PÉNDULO FÍSICO
A la distancia entre el punto de suspensión O y el centro de masa G se la llama
longitud l del péndulo físico
P
+α
Para girar un péndulo de la posición de
equilibrio II un pequeño ángulo dα
α es
necesario aplicar un momento M = P.ll.sen(α
α) (ver figura). Para ángulos
pequeños en los que el seno y el arco son equivalentes, resulta que sen(α
α)
≈α y entonces M =P.ll.α
α
I
−α
III
El trabajo exterior que debemos efectuar contra el sistema para que el péndulo ejecute una pequeña rotación dα es dL= M .dα
α = P.ll.α
α.dα
α , de manera
que la energía necesaria para llevar al péndulo a su posición de máximo
ángulo α máx resulta :
2
E =o∫α dL = ½ P.l.
l.α
αmáx
Si despreciamos el rozamiento, la energía E suministrada al péndulo se
mantendrá de aquí en más, transformándose de potencial en cinética y viceversa. Cuando el péndulo cae, va transformando parte de esa energía potencial en fuerza viva hasta llegar a su punto inferior, (α=0) en el que la
energía total es toda cinética. Luego se remonta hacia el otro lado, ganando
altura y perdiendo velocidad hasta llegar al ángulo –αmáx, situación en la que
toda la energía es potencial.
En una posición cualquiera medida por el ángulo α ≤ α máx , el péndulo tendrá una fuerza viva o energía cinética dada por la fórmula ya vista Ec = ½ J
ω2 , donde J es el momento de inercia del sólido con respecto al eje de rotación y ω = dα
α/dt es la velocidad angular instantánea, o sea el ángulo barrido en la unidad de tiempo por el eje del péndulo en el momento considerado.
La energía potencial para esa posición genérica medida por el ángulo α
resulta:
FÍSICA – DINÁMICA Y GRAVEDAD
76
U = ½ P l α2
El principio de conservación de la energía exige que la fuerza viva más la
energía potencial sea en cualquier momento igual a la energía total del
sistema, o sea
E = U+Ec , de donde E = ½ P l α2 + ½ J ω2
Tomando variaciones con respecto al tiempo en todos los miembros, nos
queda:
P.ll.α
α.ω
ω + J ω dω
ω/dt = 0 y dividiendo ambos miembros por J ω y teniendo en
cuenta que ω=dα
α/dt y que dω
ω/dt = d2α/dt2 resulta finalmente:
P.ll/J α + d2α/dt2 = 0
La ecuación anterior en la que la derivada segunda del ángulo con respecto
al tiempo, o sea la aceleración angular del movimiento, es proporcional y de
signo contrario a dicho ángulo, se satisface con una solución oscilatoria
periódica. Este hecho, por otra parte, está de acuerdo con la experiencia que
muestra que un péndulo oscila.
Entonces, ensayando como solución α = A sen (k.t) resulta
dα
α/dt = k. A. cos (k.t)
d2α/dt 2 = -k2.A..sen (k.t)
y además P.ll/J.A sen (k.t) - k2.A..sen (k.t) = 0
Esto implica que sea P.l
.l/J - k2 = 0 y por lo tanto k=√
√( P.ll/J)
Además, como el péndulo tiene velocidad cero para α = α máx y para el tiempo t = T/4 (es decir después de ejecutar un cuarto de período), resulta que
A. cos (k.t) = 0 cuando k.t=π
π/2 , de donde k.T/4 = π/2 o sea que el período
de oscilación de un péndulo físico vale
T = 2π
π/k = 2.π
π.√
√(J / P/ l)
Reemplazando el momento de inercia J = m.i2 (i = radio de inercia) y P=m.g
, la anterior queda:
2
T = 2.π
π √i / l / g
La constante A se deduce de la condición α máx = A sen (k.T/4) = A..sen(π
π /2)
de donde A=α
α máx
FÍSICA – DINÁMICA Y GRAVEDAD
77
Péndulo matemático
Se llama así al formado por una masa puntual m suspendida por una varilla
o hilo de longitud l sin peso. Para él es J = m.ll2 y entonces su período vale T
= 2π
π.√
√(J/m/g/ll) o sea T = 2π
π√ .ll/g
Se aproxima a un péndulo matemático una esfera muy densa suspendida de
un hilo largo.
lo
l
lml
lv
l
Ejemplo
Averiguar el período de oscilación de un péndulo
formado por una varilla de madera de ancho a=2
cm por un espesor ev = 1cm y de longitud l m=1m,
en cuyo extremo va un disco de cobre de radio
R=10 cm y espesor e=1 cm. La densidad de la
3
madera es 1000 Kg/m y la del cobre vale 8000
3.
Kg/m El sistema se suspende desde un punto O
situado a lO=10 cm del extremo libre de la varilla.
P
O
Gv
Pv
Pd
Pv
ld
P
G
Pd
Gd
Solución: Aplicamos lo deducido para el péndulo
físico, a saber: T= 2.π
π .√ (J / P/ l ) donde:
2
M = Masa total ; M = Vdisco.δcu + Vvarilla.δmadera = πR e.δcu + a.ev .lv.δmadera=
2,51Kg + 0,2 Kg ; P=2,71 Kg. 9,8 m/s2 = 26,56 N
l = distancia entre el centro de gravedad G del sistema y el punto de suspensión O
En la figura se ha representado el polígono funicular para encontrar el punto de aplicación G de la resultante P , en caso de desear una resolución gráfica.
Tomando momentos con respecto al punto de suspensión O podemos poner
P.l = Pd.l d + Pv.lv
De la figura resulta ld = l m-lo+r = 1-0,1+0,1=1m ;
lv = l m/2-lo = 0,5-0,1 = 0,4 m
De la expresión anterior sale que
l = (Pd.ld + Pv.lv)/P = [2,52 Kg.x1m + 0,2 Kgx 0,4m].9,8 / 2,72 Kg/9,8 = 0,956 m
J = Momento de inercia con respecto al punto de suspensión: es la suma de los momentos de inercia del disco y de la varilla. J = Jdisco + Jvarilla cada uno con respecto al
punto de suspensión.
eje y
Estudiemos ahora dos posibles
momentos de inercia baricéntricos del disco:
e
y
dy
α
R
x
eje x
La ecuación del círculo
2
2
2
x +y =R
2 2 ½
de donde x=(R -y )
es
Momento de inercia de un cuarto
de disco con respecto a un eje
radial (que pasa por el centro de
FÍSICA – DINÁMICA Y GRAVEDAD
78
gravedad), de acuerdo a la figura de la derecha
2
Jdxx/δCu/e/4 = y=0∫y=R x.y .dy
Reemplazando y=R sen α , x= R.cos α
resulta dy = R cos α dα , y entonces
Jdxx/δCu/e = a=0∫a=π/2 R cos α .R sen α cos α da =
2
∫a=π/2
a=0
4
=R
2
2
R (1-sen α) .R sen α dα =
2
∫a=π/2
a=0
2
2
2
(sen α –sen α) dα = R .[π/4 - 3π/16] = πR .R .(1/16)
2
4
4
2
2
Entonces Jdxx = (.δCu.e πR ).R .4(1/16) = M R /4 , que es el momento de inercia del
círculo con respecto a un eje baricéntrico radial.
2
2
2
Ya habíamos visto antes (cuando nos daba clases el Ing. Cattáneo) que el momento
de inercia de un disco con respecto a un eje baricéntrico perpendicular al anterior, o
2
sea el eje z, era Jzz = ½ M.R (figura de la izquierda). Resulta así Jzz = 2 Jxx
Teorema de Steiner
Pero lo que necesitamos es el momento de inercia con respecto al eje de suspensión
del péndulo paralelo al eje zz. A partir del momento de inercia baricéntrico (que pasa
por el centro de masas o baricentro), se puede encontrar el momento de inercia que
pasa por cualquier otro eje paralelo al primero, en base a la siguiente deducción debida a Jacobo Steiner, geómetra suizo que vivió en la primera mitad del siglo XIX:
El momento de inercia de un sistema con respecto a un eje que dista d del baricentro
puede ponerse como:
2
2
2
2
2
J = Σ mi.(di+d) = Σ mi (di +2di.d+d ) = Σ mi di + 2 d Σ mi.di + d Σ mi
2
El primer término Σ mi di es el momento de inercia baricéntrico, que llamaremos Jg
En el segundo término, es nulo Σ mi.di , ya que es el momento de primer orden con
respecto al baricentro. Además es Σ mi = M (masa total del cuerpo), así que
2
J = Jg + M d , lo que significa que el momento de inercia de un cuerpo con respecto a
cualquier eje se puede obtener sumando al correspondiente momento de inercia baricéntrico un término igual a la masa por el cuadrado de la distancia entre ejes.
Aplicando el teorema de Steiner resulta que el
momento de inercia del disco con respecto a un
eje paralelo al zz que pase por O es
2
2
2
Jd=J zz+Md.l d = Md ( ½ R + ld )
Reemplazando valores, se tiene Jd=2,52 Kg ( ½
2
2
2
0,1 + 1 ) = 2,533 Kg m
Momento de inercia de un prisma de base rectangular de dimensiones axe y altura l (una
varilla) con respecto un eje baricéntrico. Según
la figura, el valor de la integral doble es Jo = (1/12)
2
2
δ.e.a.l.[a .+l .] =
2
2
1/12 Mv [a .+l .]
y
l/2
dx
dy
(x 2 +y 2 )
-a/2
O
a/2
x
- l/2
a/2
Se puede considerar a la varilla formada por dos
prismas de igual base y diferente altura: uno de
e
l/2
J o=δe∫ ∫[(x 2 +y 2 ) ½ ] 2 dx.dy
x=-a/2 y=-l/2
FÍSICA – DINÁMICA Y GRAVEDAD
79
altura lo por sobre el eje de suspensión, y otro de altura (l m-lo) por debajo de éste. El
momento de inercia total de la varilla con respecto al eje que pasa por el punto de
suspensión O será de acuerdo al teorema de Steiner la suma de los respectivos momentos baricéntricos Jo1 y Jo2 más las sendas correcciones debidas al que el eje de
inercia se corre desde los centros de masa hasta la base de los prismas, que valen
2
2
respectivamente M1 lo y M2.(l m-lo) :
Entonces Jv =.M1.[1/12.(a .+lo ) + lo ] + M2.[1/12. (a +(l m-lo) ) + (l m-lo) ] para
3
M1 = δm.a.e.lo
= 1000 Kg/m . 0,02m. 0,01m; 0,1 m = 0,02 Kg
3
M2 = δm.a.e.(l m-lo) = 1000 Kg/m . 0,02m. 0,01m; 0,9 m = 0,18 Kg
Resulta entonces:
2
2
2
2
2
2
Jv = 0,02.[1/12 (0,02 +0,1 )+0,1 ] + 0,18 [1/12 (0,02 +0,9 ) + 0,9 ] =
= 0,000217 + 0,157956 = 0,158173 Kg m2
2
2
2
2
2
2
El momento de inercia total del sistema disco-varilla con respecto al punto de suspen2
sión es entonces: J = Jd+Jv = 2,533+0,158 = 2,691 Kg.m
El período del péndulo para g=9,8 m/s2 resulta T= 2.π
π .√ (J / P/ l ) = 2,0454 s
La longitud equivalente de un péndulo matemático sería l = (T/2/π) .g = 1,0397 m, es
decir que si consideramos una masa concentrada cualquiera colgada de un hilo inextensible y sin peso de longitud 1,035 m tendría el mismo período que nuestro péndulo
real de longitud total l T = ld + lo + r d = 1,2 m
2
Fenómenos Giroscópicos
Un cuerpo rígido con simetría axial presenta
fenómenos inerciales muy interesantes cuando gira sobre su eje. Todos experimentamos
alguna vez con un trompo al que hacíamos
girar rápidamente sobre su eje, y que nos
deleitaba al mantenerse parado sobre el la
punta de su eje mientras duraba la rotación.
Cuando la velocidad menguaba, el trompo
comenzaba a inclinarse y bailotear de manera muy característica. Al final
caía y rodaba sobre el piso (generalmente a un sitio inaccesible, por ejemplo
bajo el sofá).
Un trompo más elaborado es el giróscopo: una rueda pesada con un eje
sostenido por sus extremos en un bastidor. Un tirón al hilo arrollado sobre su
eje le da rápido giro. Parado sobre su eje, se comporta como un trompo. El
armazón permite que siga girando con el eje horizontal, sin que la rueda
toque el piso.
El conjunto se opone al cambio de dirección del eje, ejerciendo una reacción
en sentido perpendicular a la acción. Lo mismo que el péndulo, el giróscopo
mantiene el plano de rotación invariable con respecto a las estrellas fijas.
Esta propiedad lo hace un buen sucedáneo de la brújula, que no es afectado
FÍSICA – DINÁMICA Y GRAVEDAD
80
por campos magnéticos.
Por qué tiende a mantener su eje vertical el trompo en rotación o el giróscopo tiende a oponerse al
cambio de dirección con una insospechada reacción, son cuestiones que matemáticamente se
resuelven y explican sin dificultad, pero que contrarían nuestra intuición mecánica. A continuación
daremos una explicación más intuíble, atribuída a
20
Poggendorff . Para ello consideremos que el
giróscopo en rotación de la figura tiende a ser
volcado en el sentido de las flechas verdes (en
sentido horario). Las porciones de la rueda que
están en el plano del papel (R y S) experimentan traslaciones paralelas a su
velocidad, no obrando sobre ellas fuerza de inercia alguna. En cambio las
partes de la rueda que están adelante y atrás del plano de la rotación (P y Q)
cambian por efecto de ésta la dirección de su velocidad tangencial (flecha
blanca a flecha verde) y están sujetas a una aceleración que se ha representado por una flecha roja. Proporcionalmente a ella aparecerá una reacción sobre el conjunto que tiende a volcar el trompo hacia nosotros (flechas
anaranjadas). Si el momento volcante está creado por el peso del aparato
inclinado sobre su soporte, como se ve en la figura anterior, la reacción que
aparece en un plano perpendicular se compone con aquél
dando como resultante un movimiento llamado de precesión, en
la que el eje del trompo describe
un cono. Si el aparato recibe un
momento volcante con aceleración, la reacción también será
acelerada y el sistema oscilará
alrededor de la curva de precePRECESIÓN Y NUTACIÓN
sión, dando como resultado una
superficie festoneada cuyo contorno es una cicloide. Este movimiento se
llama de “nutación”.
La explicación matemática de la reacción giroscópica se basa en el principio de
inercia aplicado a cuerpos rotantes, equivalente al principio de Newton: así como la
fuerza F es igual a la derivada de la cantidad de movimiento con respecto al tiempo, el
momento (fuerza Ù distancia) es la derivada de el momento de la cantidad de movimiento D = m.vÙr y entonces resulta:
F=d(m.v)/dt y M =FÙr de donde M =d(m.vÙr)/dt = dD/dt
En un cuerpo rígido como el giróscopo, formado por masas elementales mi a distan2
cias ri del eje de giro que gira a velocidad angular ω =vi/ri es D=Σ
Σ mi.viÙri = Σ ω .mi.ri
20
J.G.Poggendorff, físico, químico, filósofo y médico alemán (1793-1877), quién
estudió diversas cuestiones de magnetismo, mecánica y química.
FÍSICA – DINÁMICA Y GRAVEDAD
81
=ω
ω .J, para J=Σ
Σ mi.r i (momento de inercia del cuerpo con respecto al eje de giro).
Entonces M = dD/dt = J.dω
ω /dt , lo que indica que la variación del vector velocidad
angular dω debe tener la misma dirección que el momento aplicado M . Si el momento
aplicado M es perpendicular a ω, ésta tenderá a
dω
ω ω
colocarse paralela a la primera, explicándose así
matemáticamente el origen del movimiento de
precesión
ω+dω
ω
ω+
2
Asimismo el momento de la cantidad de movimiento
D es un vector de la dirección de la velocidad angular ω , la que por otra parte coincide con la dirección del eje de giro, así que el ángulo infinitesimal
dD/D es el que gira en un tiempo dt el vector ω , o
sea que es la velocidad angular del movimiento de
M
precesión del aparato. De tal manera dicha velocidad es dD/dt/D =dω
ω /ω
ω /dt = M /J/ω
ω , lo que nos dice
que la velocidad de precesión de un giróscopo es
proporcional al momento aplicado e inversamente
proporcional al momento de inercia y la velocidad de rotación del aparato.
FÍSICA – DINÁMICA Y GRAVEDAD
82
Balanza
BALANZA DE PRECISIÓN
Se construye una balanza de precisión
suspendiendo una estructura rígida
(tipo viga reticulada) exactamente en
su punto medio, un poco por encima
de su centro de masa. En sus extremos cuelgan sendos platillos iguales.
En uno de ellos va el objeto a pesar y
en el otro van las pesas calibradas.
Los puntos de apoyo central de la viga
y los de los extremos de los platillos
son, en las balanzas de calidad, afiladas cuñas de acero duro que descansan casi sin rozamiento sobre cunas en
“v” de cuarzo. El tipo de suspensión de los platillos mediante cuñas y cunas
transmite a la viga solamente esfuerzos que pasan por esos apoyos, sin los
momentos que podrían crear cargas descentradas sobre los platillos. Todo
esto garantiza que cuando la balanza está en equilibrio las masas de los
cuerpos en ambos platillos son iguales.
L.cos α
L.cos α
O
G
P+∆P
P
α
El aparato tiene normalmente una
aguja solidaria a la viga (fiel), para
indicar desviaciones del equilibrio
sobre una escala. Esta indicación
calibrada convenientemente se
suma o resta de la masa de las
pesas para ajustar a un peso más
exacto.
En la balanza de brazos iguales de
longitud L, centro de suspensión en O ,
centro de masas de la cruz en G y masa
M, con una pequeña sobrecarga DP en el platillo derecho, la posición de equilibrio se
logra a costa de una inclinación del fiel un ángulo α de tal manera que los momentos
de las fuerzas con respecto a O se equilibren:
(P+∆P).L.cos(α) = P.L.cos (α) + M.g.GO.sen (α) , de donde ∆P.L = M.g.GO.tg (α)
La razón tg (α
α ) / ∆ p mide la desviación por unidad de peso de la balanza (sensibilidad) es directamente proporcional a la longitud de los brazos e inversamente proporcional a la masa de la cruz y a la distancia entre el centro de gravedad de la misma y
el punto de suspensión.
Una balanza equilibrada es un péndulo físico de gran momento de inercia y aunque
tiene poca distancia entre centro de gravedad y punto de suspensión (para presentar
buena sensibilidad) presenta un período relativamente elevado. Como tiene escasísimo rozamiento, sus oscilaciones se amortiguan lentamente. Para no esperar un tiempo demasiado largo a que el sistema se detenga y así conocer la posición de equilibrio
FÍSICA – DINÁMICA Y GRAVEDAD
83
de la aguja sobre la escala, se obtiene ésta indirectamente promediando varias lecturas extremas sucesivas.
Se distinguen en la balanza, como en cualquier instrumento de medida, las
siguientes características:
Exactitud, medida por la inversa del error absoluto de la medida, es decir la
diferencia entre valor medido y valor verdadero. Depende de la bondad en la
calibración de las pesas y de la igualdad y simetría entre brazos y platillos.
Precisión, medida por la cantidad de cifras exactas con las que se puede
expresar la medida. Depende de las dos siguientes cualidades.
Umbral, que es la magnitud necesaria para que el instrumento acuse una
medición no nula. Es proporcional al rozamiento en las articulaciones.
Sensibilidad, que es la razón entre lectura (en divisiones) y magnitud correspondiente (masa). Ya vimos que es función de la geometría y peso de los
elementos. La rigidez del sistema es condición para que la sensibilidad se
mantenga con la carga.
Con una balanza de laboratorio se pueden
-7
comparar masas con una precisión de 10 Kg
(una décima de miligramo), que equivale a
detectar sobre uno de los platillos una gota de
agua de tan sólo 0,6 mm de diámetro (como el
punto de esta “i”)
Existen balanzas de brazos desiguales,
llamadas “romanas”. El brazo más largo
tiene una escala y sobre él se desliza un
BALANZA ROMANA
peso, que debe estar sobre el cero de la
EN EQUILIBRIO
escala con la balanza en equilibrio cuando no hay carga sobre el platillo. Para
pesar la merluza, se la coloca en el platillo y se desliza la pesa hacia la derecha
hasta que el brazo esté horizontal. En tal
caso el sistema de fuerzas paralelas
formado por los pesos del pescado más
el platillo, el brazo izquierdo, el brazo
derecho y la pesa deslizable tiene resultante que pasa por el gancho de suspensión. La brazo del pescador que
sostiene la balanza realiza una fuerza vertical igual a la resultante, llamada
“equilibrante” del sistema.
Experiencia para determinar kG
Debajo de una balanza de platillos equilibrada con una masa de 1 Kg en
cada platillo, se coloca una gran esfera de plomo de 2 m de diámetro. La
distancia entre platillos es de 1 m y la bola está a 5 cm debajo del platillo
izquierdo. ¿Cuánto acusará de desequilibrio la balanza?
FÍSICA – DINÁMICA Y GRAVEDAD
84
En la figura se ve que a los pesos en equilibrio P que actúan debido a la
gravedad de la tierra se le suman las
1m
acciones atractivas de la bola de
plomo sobre los platillos cargados
izquierdo y derecho, que son respectivamente F1 y F2
P
1,05 m
F1
P+F2
F2
P
γ
1,45 m
β
4,189 m
3
Resulta entonces:
MPb = VPb.δPb = 4,189 m3 . 11300 Kg/m3 =
47333 Kg , por lo tanto:
F1 = kG.MPb.1/d2 =
-11
2
-6
= 6,72.10 . 47333/1,05 = 2,88.10 N
2.
F2 = kG.MPb / 1,45 =
-11
2
-6
= 6,72.10 . 47333/1,45 = 1,51.10 N
Se ha exagerado la pequeña inclinación
del platillo derecho, que forma un ángulo
γ con la vertical, siendo tg β = 1/1,05 de
donde β =43,6º
Entonces:
-6
-6
tg γ = F2.cos β / (P+ F2.sen β) = 1,51.10 .cos(43,6º)/(9,8+1,51.10 .sen(43,6º)
-6
-6
tg γ = 1,093.10 /(9,8) , de donde γ = (6,39.10 ) grados
De acuerdo al teorema del coseno es:
2
2
2
(P+F2) = P +F2 +2.P.F2.cos (β) =
2
-6 2
-6
= 9,8 + [1,51.10 ] +2.9,8.1,51.10 .
cos(43,6º)= 96,040021 N
de donde P+F2 = 9,800001094 N
Como P y F1 están en la misma
dirección es:
-6
|P+F1|= P+F1 = 9,8+2,88.10
=
9,80000288 N
lo
δ
O
P+F2
G
P+F1
En la figura se esquematiza la
posición de equilibrio, cuando las
fuerzas en los platillos y el peso
de la balanza M.g aplicado en el
centro de gravedad G dan una
resultante R que pasa por el eje
de giro de la balanza O
l
l
γ
R
R
M.g
δ
La balanza indicará aproximadamente la diferencia entre las dos fuerzas, ya
que ellas están prácticamente en el misma dirección vertical, o sea:
-6
-7
9,80000288 - 9,800000151 = 1,79.10 N = 1,82.10 Kg
Esta diferencia de casi dos décimas de miligramo es bastante superior al
umbral de la balanza y por lo tanto perfectamente apreciable.
FÍSICA – DINÁMICA Y GRAVEDAD
85
La experiencia se realiza en forma práctica equilibrando los dos platillos con
masas iguales sin la presencia de la bola y observando la deflexión del fiel al
deslizar aquélla debajo de uno de los platillos. Se comprende así que dicha
deflexión sea causada por la diferencia entre
F1= 2,88.10-6N y la proyección vertical de F2, que vale
F2.cos (β) = 1,093.10-6 N , o sea ∆F = 1,79.10-6N
La componente horizontal de F2 crea un momento que produce la imperceptible inclinación del platillo derecho en un ángulo γ con respecto a la vertical
ya calculado antes.
Este experimento fué realizado como se
acaba de explicar, con una balanza común, por el físico inglés Poynting en
1913. De la medida de ∆F se deduce el
valor de la constante kG
Anteriormente otros dos ingleses, Cavendish a fines del siglo XVIII y Boys a fines
EXPERIENCIA DE CAVENDISH
α
del XIX habían medido la atracción gravitatoria de dos grandes masas fijas sobre un par de masas más pequeñas
colocando éstas sobre una varilla horizontal sostenida por un hilo de cuarzo,
que resiste levemente a la torsión producida por el par de atracciones. Las
pequeñas deflexiones del sistema se detectan con un rayo de luz reflejado
en un espejito solidario a la varilla. El haz de luz reflejada gira el doble del
ángulo barrido por la varilla con las dos masas y se proyecta sobre una
pantalla alejada, amplificando así la desviación del sistema móvil.
2α
α
El problema del tiro
Tiro en el vacío
Ya se vió que la trayectoria de un proyectil en el vacío bajo un campo gravitatorio
paralelo es una parábola. El estudio del problema puede encararse adecuadamente
aplicando las leyes de la dinámica de Newton independientemente para la coordenada
horizontal (x) y la coordenada vertical (y), y superponer los efectos en virtud del principio de superposición. Así resulta que para una partícula de masa m y aceleraciones
2
2
2
2
vertical y horizontal respectivamente iguales a d x/dt y d y/dt se pueden plantear las
siguientes ecuaciones:
2
2
fx = m.d x/dt = 0 , ya que es nula la fuerza
y
horizontal aplicada sobre la partícula en movivo
miento.
αo
v
vy
vx
x
De aquí se deduce que la velocidad horizontal
es constante, o sea, Þ vx = dx/dt = constante =
vox (velocidad horizontal inicial) = vo.cos (α).
Integrando sale que:
x-xo = vo.cos(α
α ).t
[1]
FÍSICA – DINÁMICA Y GRAVEDAD
86
De la misma manera, igualando la masa por la aceleración vertical al peso de la partícula (única fuerza actuante) resulta:
2
2
fy = m.d y/dt =-m.g, Þ dy/dt = - g.t+C
La constante de integración C resulta de considerar que v=v0 cuando t=0, e y=y0
C = dyo/dt = voy (velocidad vertical inicial)= vo.sen(αο)
2
y-y o = - ½ g.t + vo.sen(α
αο ).t
[2]
Como se ve, [1] y [2] son las ecuaciones paramétricas de una parábola de eje vertical
que pasa por el punto de disparo del proyectil, de coordenadas (x0, y0)
Tiro en el seno de un fluído
Cuando el proyectil se mueve en el seno de un fluído quieto, por ejemplo el
aire calmo, el medio produce una resistencia o fuerza contraria a la velocidad
de la partícula, como se explica luego en esta obra al tratar la mecánica de
fluídos. La dependencia entre resistencia y velocidad es una combinación de
dos efectos: el de rozamiento viscoso y el efecto inercial del desplazamiento
del fluído creado por el paso del móvil. El primero es preponderante a velocidades bajas (régimen laminar) y el segundo es más importante a velocidades altas (régimen turbulento). Estudiaremos ambos por separado.
Resistencia viscosa proporcional a la velocidad (modelo de Stokes)
En este caso la fuerza de sentido contrario a la velocidad, viene dada por la fórmula de
Stokes, tratada in extenso en este libro más adelante.
fv = [4.π.η
π.η.r].v = b.v , donde:
21
η=viscosidad ; r=radio del proyectil que se supone de forma esférica. Este modelo
tiene sólamente en cuenta la resistencia viscosa y no la inercial.
Para la componente horizontal vale el siguiente desarrollo:
2
2
2
2
fx = m.d x/dt + b.vx = 0 ; d x/dt = dvx/dt=-(b/m).vx, Þ ln(vx) = -(b/m).t + ln(vox)
[-(b/m).t]
vx = v.cos(α) = vox.e
(que indica que la velocidad decrece exponencialmente con
el tiempo)
[-(b/m).t]
[-(b/m).t]
vox.e
= dx/dt Þ x = ò vo.cos(αο).e
dt + C =
[-(b/m).t]
= vo.cos(αο).(-m/b).e
+ C1 Þ C1 = xo + vo.cos(αο).m/b
-(b/m).t
x-xo = vo.cos(α
αο ).(m/b).(1- e
)
Considerando la acción vertical de la gravedad resulta:
2
2
2
2
fy = m.d y/dt + b.vy = - m.g ; d y/dt = dvy/dt = -(b/m).vy – g
Sea u = (b/m).vy + g Þ du=-(b/m).dvy Þ dvy/dt = (-m/b).du/dt = u Þ du/u = (-b/m).dt
(-b/m).t
Integrando se obtiene ln(u)= (-b/m).t + ln(uo) Þ u=uo.e
(-b/m).t
(-b/m).t
(b/m).vy + g = [(b/m).voy+ g]. e
; vy = (m/b).[(b/m).voy+ g]. e
- (m/b).g = dy/dt
Integrando nuevamente resulta:
(-b/m).t
y=(-m/b).(vo.sen(α).b/m+g).(m/b).e
– g.m/b.t + C2
2 2
C2 = yo + m/b.vo.sen(αo) + g.m /b
2 2
-b/m.t
y-y o = (vo.sen(α
α o).m/b + g m /b )(1-e
)-g.m/b.t
21
Como se explica al estudiar los fenómenos de movimiento interno en un fluído, la
viscosidad mide la resistencia al deslizamiento entre capas próximas del mismo, y es
proporcional a la velocidad relativa entre ellas.
FÍSICA – DINÁMICA Y GRAVEDAD
87
Resistencia inercial proporcional al cuadrado de la velocidad
(modelo de Newton)
Como se explica en esta obra al tratar sobre la resistencia de objetos en movimiento
dentro de un fluído, se emplea la fórmula de Newton para la fuerza de resistencia
cuando predomine el efecto inercial, que depende del peso específico y no de la viscosidad del fluído:
2
2
fv = [k.ρ
ρ/2/g.S].v = b’.v (fórmula de Newton)
k = coeficiente de forma (por ejemplo, para una esfera es k = 0,4)
ρ = peso específico del fluído
S = superficie de carena, o sea la proyección del cuerpo sobre un plano perpendicular
a la velocidad.
Horizontalmente sólo actúa la fuerza de resistencia:
2
2
2
2
2
2
fx = m.d x/dt + b’.vx = 0 ; d x/dt = dvx/dt=-(b/m).vx , Þ -1/vx = C3 –b’/m.t ; C3=-1/vox
vx = 1/(b’/m.t+1/vox) =dx/dt = dx/dt ; dx = dt/(b’/m.t+1/vox) = (m/b’) d(b’/m.t+1/vox)/(b’/m.t1/vox)
dx = (m/b’) d ln (b’/m.t+1/vox) Þ x = (m/b’) . ln (b’/m.t+1/vox) + C4
C4 = xo - (m/b’).ln (1/vox)
x-xo = (m/b’) .[ln (b’/m.t+1/v ox) - ln (1/v ox)]
Para la dirección vertical, interviene además la fuerza de gravedad m.g :
2
2
2
2
2
2
fy = m.d y/dt + b’.vy = -m,g ; d y/dt = dvy/dt=-(b/m).vy -g
2
½ 2
2
½
½
2
dt= -dvy/(g+vy .b’/m)= -dvy/[g(1+vy .b’/m/g)]= -(m/g/b’) .d[vy .(b’/m/g) ]/(1+[vy .(b’/m/g) ] )
Integrando resulta
½
½
½
– (g.b’/m) .t = arc tg [vy.(b’/m/g) ] -C5 Þ C5=arc tg [vo.sen(α
α o).(b’/m/g) ]
Sacando la tangente en ambos miembros queda:
½
½
½
½
[vy.(b’/m/g) ] = tg {arc tg [vyo.(b’/m/g) ] – (g.b’/m) .t)} = tg [C5-(g.b’/m) .t)]
½
½
vy = dy/dt = (m.g/b’) .tg [C5-(g.b’/m) .t)]
½
½
½
y = (m.g/b’) òtg [C5-(g.b’/m) .t)].dt + C6 = (m.g/b’) I + C6
½
½
½
½
I =òtg [C5-(g.b’/m) .t)].dt = -(m/g/b’) òtg [C5-(g.b’/m) .t)].d [C5-(g.b’/m) .t)] =
½
½
= -(m/g/b’) {-ln cos [C5-(g.b’/m) .t)]}
½
y = (m/b’).ln cos [C5-(g.b’/m) .t)] + C6
C6 = yo - (m/b’).ln cos [C5]
Tiro en medios fluídos
Stokes
Newton
vacío
0,3
0,25
0,2
0,15
0,1
0,05
0
-0,05 0
-0,1
-0,15
-0,2
-0,25
0,2
0,4
0,6
0,8
1
Se puede observar en la figura las
trayectorias de tiro que surgen de
representar gráficamente las ecuaciones según los modelos de Stokes y de
Newton para una bolita de hierro de 1
cm de diámetro en un medio aceitoso,
lanzada a una velocidad inicial de 3
m/s y con un ángulo de 45º. La trayectoria real se acerca más a la de
Stokes, en este caso, por tratarse de
un medio de alta viscosidad.
FÍSICA – DINÁMICA Y GRAVEDAD
88
En torno a la gravedad
Las ecuaciones del movimiento de un proyectil en el vacío con campo gravitatorio
constante dan una parábola. Sin embargo
esto es sólo una aproximación aceptable
para el caso de proyectiles de corto alcance, para los que la tierra es prácticamente
plana. Como vimos cuando tratamos el
modelo fluído, la gravedad creada por un
plano material es de líneas de campo perpendiculares a la superficie y paralelas
22
entre sí . En cambio, en el caso que se
muestra en la figura que acompaña debe
tenerse en cuenta que la curvatura de la TRAYECTORIAS DE PROYECTILES BALÍSTICOS
tierra impone al campo gravitatorio líneas radiales que se sumen en el centro
de la esfera. La densidad de líneas de campo gravitatorio en una zona es
23
proporcional a su intensidad . Cuando los proyecB
tiles son de largo alcance, su trayectoria se aleja lo
suficiente como para que las líneas de campo sean
sensiblemente menos densas. El campo gravitatorio
A
radial hace que la parábola, que es una curva
abierta, se transforme en elipse, que es una curva
cerrada. Uno de los focos de esa trayectoria elíptica
es el centro de la tierra, como se vió al tratar movimiento central.
En el dibujo adjunto se ve que a un campo paralelo (líneas verdes) producido
por un cuerpo de superficie plana ilimitada (verde), le corresponde una trayectoria parabólica (roja). En cambio, a un cuerpo esférico (gris), con líneas
de campo convergentes en el centro (negras) le corresponde una trayectoria
elíptica (verde), que parte de A con la misma inclinación.
Si la tierra fuera más chica con igual masa y manteniendo su centro, y pasara de la esfera gris a la interior rojo oscuro, se estaría ante una tierra más
densa. En tal caso la trayectoria elíptica verde del proyectil se mantendría y
no cortaría a la esfera reducida. Para que ello ocurriera y el proyectil se
transformara en un satélite artificial, se lo debería lanzar con idéntica velocidad que antes desde el mismo punto A, que ahora quedaría fuera del planeta, a gran altura.
22
Un campo de líneas paralelas es constante en todos sus puntos
La densidad de líneas en el caso de campo radial es inversamente proporcional al
cuadrado de la distancia, lo cual autoriza precisamente a adoptar el modelo del “fluído
gravitatorio” con sumidero en las masas.
23
FÍSICA – DINÁMICA Y GRAVEDAD
89
Precisamente, para poner en órbita un artefacto se lo eleva casi verticalmente con un cohete a altura conveniente. Desde allí, con otro cohete, se le
imparte velocidad horizontal suficiente como para que siga libremente describiendo una trayectoria que no intercepte a la tierra, siguiendo una órbita
de magnitud y excentricidad adecuadas al servicio que prestará el ingenio
(comunicaciones, imágenes, espionaje, etc.) . En la jerga de cohetería espacial, se llama a esta velocidad “de inserción” en la órbita.
En el caso de una órbita circular de radio R, el artefacto describe un movimiento circular uniforme de velocidad tangencial v tal que la fuerza centrífuga Fc = m.v2/R equilibre a la atracción gravitatoria Fg = kG.MT.m / R2 , es decir
v = (kG.MT/R) ½ , o bien, considerando que g=kG.MT/RT2 , la anterior puede
ponerse bajo la forma v = [(kG.MT/RT2).RT2/R] ½ = RT .g ½ / R ½
La velocidad angular será ω = v/R = RT .g ½ / R 3/2
Por ejemplo: Se desea poner en órbita un satélite ecuatorial que se mantenga fijo en
el cielo. A qué velocidad horizontal y a qué altura debe lanzarse?.
La condición de que se mantenga fijo en el cielo determina su velocidad angular, que
debe ser igual a la de la tierra, es decir
-5
ω = 2.π/24/3600 = 7,27.10 rad/s
Además es R = (R T g / ω) = (6378000 m . 3,13 m .s / 7,27.10 s )
= 42238 Km , o sea que orbitará a una altura de 35860 Km
½
2/3
½
-1
-5
-1 2/3
=
La velocidad de inserción horizontal que debe impartirle el segundo cohete vale
v = ω.R= 7,27.10-5. 42238 Km = 3,1 Km/s = 11054 Km/h
Transitando por la gravedad
Para mover una masa a través de un camino en un campo como el gravitatorio, donde las líneas sólo mueren sumiéndose en la materia, hay que ejecutar un trabajo que es el resultado de sumar trabajos elementales (producto
escalar de fuerza por elemento de camino o longitud ∆l): T= Σ F.∆
∆ l , cuyo
valor no depende más que del punto de partida y el punto de llegada, sin
importar por dónde pasa el camino que recorre la fuerza. Esto es así, debido
a que el campo (o aceleración gravitatoria) es la pendiente de una función
del espacio llamada potencial, análoga al nivel de un terreno en el que la
materia es una depresión. Así como el terreno alrededor de un hoyo tiene
líneas de nivel y líneas de máxima pendiente, el espacio alrededor de una
masa tiene superficies de igual potencial y líneas de campo. Éstas son las
trayectorias que seguirían masas exploratorias abandonadas en diferentes
puntos del espacio.
FÍSICA – DINÁMICA Y GRAVEDAD
90
Se puede construir fácilmente un símil topográfico de un sistema gravitatorio
colocando una esfera pesada sobre un tejido elástico o membrana tirante. La
depresión que provoca su peso sobre el tejido se propaga en el espacio
como un campo gravitatorio.
SÍMIL TOPOGRÁFICO DE LA GRAVEDAD
Si se lanza convenientemente
una bolita alrededor de la masa,
girará alrededor de ella en forma
muy parecida a un satélite alrededor del cuerpo que ejerce una
24
atracción gravitatoria , o eventualmente pasará de largo con
una trayectoria hiperbólica si el
impulso inicial es suficiente.
líneas de nivel = líneas equipotenciales
líneas de máxima pendiente = líneas de campo
Como dijimos, el trabajo necesario para llevar un masa m desde un punto A
a otro B dentro de un campo gravitatorio creado por una masa M está medido por la energía EAB = A∫BF.dll (integral de un producto vectorial)
F=kG.M.m/r2 y siendo dll el desplazamiento elemental .
25
B
A’
-6
-5
B’
-4
rA
A
-3
-2
-1
rB
para
Nótese que el campo se sume paralelamente a la superficie de la materia (en este
caso de forma irregular) que lo produce.
Sin embargo a una distancia grande comparada con las dimensiones del cuerpo, las
líneas son sensiblemente radiales como si
fueran a parar al centro de masas de
aquél. Por supuesto que si el cuerpo
atractor es esférico y homogéneo, el campo es siempre radial, a cualquier distancia
de su centro de masas.
En el dibujo, las líneas azules son las de
campo (líneas de fuerza) y las anaranjadas son las líneas de igual potencial,
que en realidad son las intersecciones con el plano del dibujo de las superfi24
La órbita de la bolita es una curva alabeada (no plana) a diferencia de la órbita
gravitatoria y es comparable con ésta sólo su proyección vertical, que sería una elipse
si no hubiera rozamiento. A causa de éste, es un espiral elíptica que termina al precipitarse en el hoyo, junto a la esfera mayor.
25
Esa integral de línea (a lo largo de un camino) de un vector se llama circulación
entre los límites A y B. Cuando el vector es una fuerza, la circulación se llama trabajo.
Cuando es un campo conservativo (sin fuentes ni sumideros a lo largo del camino), se
llama diferencia de potencial. El gradiente del potencial es el campo en el punto considerado. La circulación en un camino cerrado es nula si el campo es conservativo.
FÍSICA – DINÁMICA Y GRAVEDAD
91
cies cerradas que rodean a la materia para las cuales el potencial es igual en
todos sus puntos (superficies equipotenciales).
El trabajo necesario para alejar una masa m entre A y B es el mismo recorriendo cualquier camino que una esos puntos, de la misma forma que para
llevar un peso por la ladera de una montaña: lo que cuenta es la diferencia
de nivel entre puntos inicial y final.
Por ejemplo, por el camino directo (en negro) la integral vale lo mismo que
por el rojo o por el verde. En estos últimos hay una parte en la que el trabajo
es nulo, de A a A’ y de B’ a B. En estos tramos el producto vectorial se
anula por ser F perpendicular a la trayectoria. Queda como trabajo el realizado entre A y B’ o lo que es igual, el realizado entre A’ y A, trayectorias
ambas en las que la fuerza tiene la misma dirección de la trayectoria, y por lo
tanto el producto escalar de los vectores fuerza y distancia se transforma en
producto de los módulos de ambos vectores, es decir
EAB = A∫B’F.dll = kG.M.m A∫B’ dr/r2 = kG.M.m [1/rA - 1/rB] = m.(UA – UB) siendo U el
potencial del punto respectivo
El potencial varía inversamente a la distancia siempre que r sea grande
comparada con las dimensiones de la masa, es decir que el campo pueda
considerarse radial. Así es Ur = kG.M/r
Como rA < rB el trabajo es positivo, es decir que hay que entregar trabajo
para alejarse de la masa atractora.
Se ve también que el potencial es nulo a gran distancia de la masa, o sea
para r→ ∞ . El significado físico de esta consecuencia matemática es una
fuente de gravedad muy lejos de las masas, desde donde provienen las
líneas que se sumen en ellas. El símil topográfico de esta configuración de
líneas y potenciales sería una planicie al nivel del mar afectada por un hundimiento localizado, o en el modelo hidráulico, una pileta enorme que nunca
se vacía a pesar del agua que sale por un sumidero colocado en un nivel
más bajo que la superficie.
Escapando de la gravedad
No todo lo que sube tiene que bajar forzosamente. Se puede impartir a un
proyectil la energía necesaria para que venza la atracción gravitatoria, y aún
la supere, yéndose definitivamente de nuestro lado para nunca más volver.
Analicemos esta proposición con reminiscencias de tango desde el punto de
vista físico:
FÍSICA – DINÁMICA Y GRAVEDAD
La energía necesaria para
escapar con un cuerpo de
masa m de la gravedad
generada por un cuerpo
de masa M es:
EA∞ = A∫ F.dll =
∞
92
TIRO DE ARTILLERÍA Y VELOCIDAD DE ESCAPE
v>vc : HIPÉRBOLA
v=vc : PARÁBOLA
v<vc : ELIPSE
= kG.M.m A∫ dr/r2 =
= kG.M.m [1/rA] = m.UA
Si quisiéramos escapar
con un artefacto de masa
m de la gravedad de la
tierra, de masa M y radio
rT, deberíamos suministrarle un trabajo que es
asíntotas de la hipérbola
igual a la variación de
fuerza viva:
Ec = ½ m ve2 = kG.M.m [1/rT] de donde ve = (2.kG.M/rT) ½ ,
y dado que g=kGM.m/rT2 es entonces
ve=(2.g.rT)½=(2.9,8.6378000)½= =11181 m/s
∞
A esta velocidad se la llama “velocidad de escape”, y es la que debe poseer
como mínimo un proyectil en la superficie de la tierra para escapar a la gra26
vedad . Sale así de la trayectoria elíptica (cerrada) para pasar a una trayectoria abierta, que puede ser parabólica cuando la velocidad del proyectil
es igual a la de escape e hiperbólica cuando es mayor que ésta. Se demuestra que en todos los casos las trayectorias cónicas citadas tienen sus
focos en el centro de la tierra.
El astrónomo alemán Karl Schwarzschild predijo en 1916 la existencia de cuerpos
celestes que provenían de la evolución de estrellas que se comprimían bajo el efecto
gravitatorio de su propia materia. Si el campo gravitatorio propio de estos cuerpos
celestes es tan intenso que la velocidad de escape iguala a la de la luz, ésta, que tiene
una masa asociada y por lo tanto es afectada por la gravedad como cualquier cuerpo,
no podrá escapar fuera de la influencia del astro, y éste será invisible para los de otros
½
8
mundos. Esto se cumple cuando ve = (2.kG.M/r T) = c (velocidad de la luz = 3.10 m/s)
La relación masa/radio necesaria para que un cuerpo no pueda emitir luz por
2
16
-11
26
efecto gravitatorio es M/RSch = c /2/kG = 9.10 /2/(6.72.10 ) = 6,7.10
El radio correspondiente para un cuerpo esférico de masa M cuya velocidad de escape sea la de la luz se llama “radio de Schwarzschild”. Para el caso de al tierra vale:
24
26
RSch = 5,98 10 Kg / 6,7 10 = 8,9 mm (dimensiones de una bolita como la que se usa
para jugar al “hoyo”)
26
La velocidad de escape es la que tendría un cuerpo en caída libre desde una altura
igual al radio terrestre si su aceleración g se mantuviera constante, es decir si el campo fuera paralelo (cosa que en realidad no se cumple).
FÍSICA – DINÁMICA Y GRAVEDAD
93
Energía asociada a la gravedad
Un sistema de dos masas posee energía de forma (potencial) intrínseca, que
proviene del trabajo realizado para colocarlas a cierta distancia. Si consideramos que “formamos” el sistema trayendo los cuerpos desde el infinito (o
sea desde potencial cero) hasta la distancia r, habrá que ir aguantando la
atracción gravitatoria durante el acercamiento, obteniendo así energía en vez
de suministrarla. Es decir que la energía de configuración de dos masas a
cierta distancia es negativa.
Desde ese punto de vista, una masa concentrada en un volumen de dimensión R supone una energía negativa de formación, si consideramos que está
formada por acreción (agregado) de partículas de masa elemental dm que
descienden a un hoyo de potencial cada vez más profundo, proporcional a la
masa acumulada y a la inversa del radio de acreción. Se puede entender
este proceso gradual de formación comparándolo don el de la construcción
de un pozo de profundidad R del que se extrae una cantidad total de tierra M
con baldecitos que contienen una cantidad dm. Extraer el primero requiere
un trabajo mínimo. A medida que el pozo se profundiza, cada balde se debe
subir desde más abajo. Se demuestra que el trabajo total es la mitad del que
supone subir toda la tierra desde el fondo M.g.R, es decir M.g.R/2. Del mismo modo, la energía para “armar” una masa M con elementos dm sobre una
esfera de radio R es la mitad de la que se requiere para traer esa masa desde potencial cero hasta el potencial kG.M/R , es decir -½.kG.M 2/R (con signo
27
negativo).
Para los que prefieren el cálculo infinitesimal a los razonamientos analógicos, el resultado anterior sale de integrar dos veces la fuerza elemental de
segundo orden d2F = kG/r2.dm2 por la distancia dr , entre los límites m=0 a
m=M , y entre r=∞
∞ a r=R , es decir EG = kG ∫ ∫ ∫1/r2dm.dm.dr
La energía de configuración asociada a una masa m es por lo tanto negativa,
y se puede considerar que está distribuida en el campo gravitatorio cuyo
valor en función de la distancia vale g(r)=kG.M/r2.
Una esfera hueca de masa m y radio r produce un campo sobre su superficie que vale g(r)= kG.m/r2 (igual que una masa m concentrada en el centro).
Si su radio se contrae en dr dejará libre un volumen dV = 4.π.r2.dr , ocupado
con el campo gravitatorio, a costa de un trabajo negativo
dE = m.g(r).dr = -kG.m2/r2.dr
La energía por unidad de volumen de campo gravitatorio vale
dE/dV = -kG/4/π
π.m2/r4 = - 1/(4π
πkG)g(r)2
27
Se demuestra que para acumular esa masa dentro de un volumen esférico en vez
2
de una cáscara de espesor infinitesimal, el trabajo es algo mayor que ½ kG.M /R
FÍSICA – DINÁMICA Y GRAVEDAD
94
Es decir que la densidad volumétrica de energía contenida en el espacio
afectado por un campo gravitatorio es negativa y proporcional al cuadrado
del valor de dicho campo.
Vemos así que el campo gravitatorio, imaginado inicialmente como mera
construcción físicomatemática para modelizar el mecanismo de la transmisión de fuerzas a distancia, adquiere ahora una nueva jerarquía, cercana a la
de la materia que le da origen, con la propiedad de tener energía negativa
28
asociada .
28
El Ing. Rodríguez de Bello y otros han desarrollado una teoría que contempla los
efectos gravitatorios al asignar un equivalente de masa negativa a la correspondiente
energía negativa del campo gravitatorio.
FÍSICA – DINÁMICA Y GRAVEDAD
a
-o-o-o-
FÍSICA GENERAL
ÍNDICE TEMÁTICO DE LA SEGUNDA PARTE
DINÁMICA Y GRAVEDAD
DINÁMICA (movimiento bajo la acción de fuerzas)..............................39
Fuerza............................................................................................39
Masa..............................................................................................39
Cantidad de movimiento .................................................................39
Interacción de la materia........................................................................39
Ley de conservación de la cantidad de movimiento.............................39
Interacción entre cuerpos ...................................................................40
Centro de gravedad de un sistema de masas...............................40
Acciones de las fuerzas .........................................................................41
Fuerzas exteriores e interiores a un sistema de masas........................41
Jugando al billar – Primera parte.....................................................41
Efectos de las fuerzas ........................................................................42
Trabajo de una fuerza............................................................................43
Energía de un sistema...........................................................................43
Tipos de energía................................................................................44
Energía cinética - Teorema de la fuerza viva ...................................44
Energía potencial............................................................................45
Sistemas de fuerzas conservativas ..............................................45
Sistemas de fuerzas NO conservativas ........................................46
Principio de conservación de la energía - Calor y Termodinámica........47
Jugando al billar – Segunda parte.......................................................49
Choque elástico y plástico ..............................................................50
Coeficiente de restitución ............................................................50
Choque elástico ..........................................................................51
Choque oblicuo ...........................................................................52
Choque plástico ..........................................................................53
Mecánica de los cuerpos rígidos ............................................................53
Concepto de cuerpo rígido .................................................................53
Centro de masa de los cuerpos rígidos. ..............................................54
Fuerza viva de los cuerpos rígidos......................................................55
Momento de inercia ........................................................................55
Cálculo del momento de inercia de un cilindro de radio R y altura L
con respecto a su eje ..................................................................56
Crónicas del CNBA..................................................................56
Cuerpos rígidos sometidos a fuerzas ..................................................57
Resultante de un conjunto de fuerzas aplicadas a un cuerpo rígido..58
Problema general en el espacio...................................................58
Problema en el plano ...............................................................59
Método del polígono funicular...................................................59
FÍSICA – DINÁMICA Y GRAVEDAD
b
Justificación del método del polígono funicular ......................... 60
Momento de una fuerza con respecto a un punto ............................ 61
Casos en que el momento de una fuerza
con respecto a un punto es nulo .............................................. 61
Momento y Trabajo.................................................................. 61
Momento de un sistema de fuerzas.......................................... 62
Momento de una cupla................................................................ 63
Composición de fuerzas paralelas aplicadas al cuerpo rígido........... 64
Fuerzas concentradas y distribuídas................................................... 65
Gravedad ................................................................................................. 67
Peso.................................................................................................. 67
Centro de gravedad ........................................................................... 68
Ley de la gravedad ............................................................................ 68
Gravedad en la superficie de un cuerpo .......................................... 70
Alcance de la ley de gravitación ......................................................... 71
Fuerzas a distancia – Campo y potencial gravitatorio ............................. 71
Campo gravitatorio ............................................................................ 72
Teorema de Gauss......................................................................... 73
Gravedad en acción........................................................................... 73
Caída de los cuerpos – Masa inercial y gravitatoria ......................... 74
Péndulo ......................................................................................... 74
Péndulo matemático ................................................................... 77
Fenómenos Giroscópicos................................................................... 79
Balanza.......................................................................................... 82
Experiencia para determinar kG ................................................... 83
El problema del tiro ........................................................................ 85
Tiro en el vacío ........................................................................... 85
Tiro en el seno de un fluído ......................................................... 86
En torno a la gravedad....................................................................... 88
Transitando por la gravedad............................................................... 89
Escapando de la gravedad................................................................. 91
Energía asociada a la gravedad ......................................................... 93
FÍSICA – DINÁMICA Y GRAVEDAD
c
ÍNDICE ALFABÉTICO DE LA SEGUNDA PARTE
acción a distancia, 67
aceleración centrífuga del
movimiento, 69
aceleración de la gravedad, 67
Aconcagua, 67
acreción, 93
analogía fluída (gravitación), 73
arco de alambre, 68
atracción gravitatoria. Véase
gravedad
atracciones y repulsiones
magnéticas, 71
balanza, 82
baricentro, 40, 55, 67
billar (jugando), 41, 49
bolitas (juego), 51
Boys (determinaciónde kG), 85
Buenos Aires, 67
caída de los cuerpos, 73
calor, 44, 47, 49
campo de fuerzas conservativo,
46
campo eléctrico, 72
campo gravitatorio, 72, 73
campo magnético, 72
cantidad de movimiento, 39
cantidad de movimiento
(conservación), 39
carena (superficie de carena), 87
Carnot, 49
carrito, 42
Cavendish (determinación de kG),
85
centro de gravedad, 40, 67
centro de masa, 54
centro de masas, 40, 67
chapa, 68
choque elástico, 51
choque elástico y plástico, 50
choque oblicuo, 42, 52
choque plástico, 53
choque recto, 42
coeficiente de restitución, 50
cohete (satélite), 89
composición de fuerzas paralelas,
64
configuración del sistema
(energía), 45
conservación de la energía, 47
crónicas del CNBA, 56
cuerpo rígido, 53
cupla, 63
densidad, 66
desagüe (flujo de agua), 72
determinación de kG, 83
diferencia de potencial, 46
dinámica, 39
dinamómetro, 60
ecuación del péndulo, 76
elipse, 88
energía (tipos), 44
energía cinética, 44, 45, 48
energía de configuración, 47
energía de un péndulo, 75
energía de un sistema, 43
energía interna, 48
energía muscular, 47
energía negativa (campo
gravitatorio), 93
energía potencial, 45, 48
energía térmica, 47
esfuerzo muscular, 39
evoluciones, 47
exactitud (balanza), 83
experiencia de Joule, 45
fenómenos giroscópicos, 79
fuentes del campo, 46
fuentes y sumideros (gravedad),
71
fuerza, 39
fuerza de gravedad, 67
fuerza viva. Véase energía
cinética
fuerza viva (cuerpo rígido), 55
fuerza viva de rotación, 55
fuerza viva de traslación, 55
fuerzas (efectos), 42
fuerzas a distancia, 71
FÍSICA – DINÁMICA Y GRAVEDAD
fuerzas concentradas, 58
fuerzas concentradas y
distribuídas, 65
fuerzas conservativas, 45
fuerzas coplanares, 59
fuerzas distribuídas, 58
fuerzas en el espacio, 58
fuerzas entre cuerpos
electrizados, 71
fuerzas exteriores e interiores, 41
fuerzas no conservativas, 47
función potencial, 89
gasto, 72
Gauss (teorema), 73
giróscopo, 79
gravedad, 46, 67
gravedad (en torno a la), 88
gravedad (energía asociada a la),
93
gravedad (escapando de la), 91
gravedad (transitando por la), 89
gravedad en acción, 73
gravedad y distancia, 69
gravitación universal
(constante de), 70
inercia, 43
interacción (materia), 39
Joule (unidad), 43
ley de gravitación, 68
ley de gravitación (alcance), 71
líneas de corriente, 72
líneas de fuerza (campo), 46
lugar de aplicación (fuerza), 58
luna, 68
manzana (Newton), 68
masa, 39
masa concentrada, 53
masa distribuída, 53
masa inercial y gravitatoria, 74
memoria de forma, 47
modelo topográfico (campo), 46
momento de inercia, 55
momento de inercia (péndulo),
76, 77, 79
momento de inercia de un
cilindro, 56
d
momento de inercia de un disco,
78
momento de inercia de un prisma
de base rectangular, 78
momento de inercia del círculo,
78
momento de la cantidad de
movimiento, 80
momento de primer orden, 65
momento de segundo orden.
Véase momento de inercia
momento de un sistema de
fuerzas, 62
momento de una cupla, 63
momento de una fuerza, 61
momento y trabajo, 61
movimiento central, 69, 88
Newton, 68, 80
Newton (resistencia inercial), 87
Newton (unidad de fuerza), 39
nutación, 80
órbita (satélite), 89
órbita de la luna, 69
parábola, 88
parábola de tiro, 85
paralelogramo de fuerzas, 59
partículas materiales, 58
péndulo, 74
péndulo físico, 74
péndulo físico y balanza, 82
péndulo matemático, 77
período del péndulo, 75
peso, 67
peso de los objetos, 73
plomo, 83
Poggendorff (giróscopo), 80
polígono funicular, 59, 64
potencial, 46
potencial nulo, 91
Poynting (determinación de kG),
85
precesión, 80
precisión (balanza), 83
presión, 39, 66
presión del viento, 65
primer principio de la
FÍSICA – DINÁMICA Y GRAVEDAD
Termodinámica, 49
principio de conservación de la
masa-energía, 48
principio de inercia, 74
propiedades del espacio, 44
proyectil (movimiento), 88
punto de aplicación, 58
reacción giroscópica, 80
recta de acción, 58
resistencia del aire, 43
resistencia viscosa, 47
resorte, 45
resorte (trabajo), 47
restitución (coeficiente), 50
resultante, 58
Rodríguez de Bello (gravitación),
94
romanas (balanza), 83
rozamiento, 43, 47
satélite artificial, 88
Schwarzschild (radio de), 92
sensibilidad (balanza), 83
e
símil topográfico de la gravedad,
90
Steiner (teorema de), 78
Stokes (resistencia viscosa), 86
Sucre, 67
sumideros del campo, 46
tango, 91
termodinámica, 47
tierra, 69
tierra (curvatura), 88
tiro en el seno de un fluído, 86
tiro en el vacío, 85
trabajo de una fuerza, 43
trayectorias de tiro, 87
trompo, 79
umbral (balanza), 83
vector momento, 63
velocidad angular (péndulo), 75
velocidad de escape, 92
velocidad de inserción (satélite),
89
velocidad de precesión, 81