tema 4: cinemática del punto material

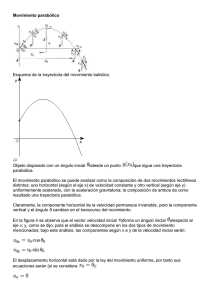
TEMA 4: CINEMÁTICA DEL PUNTO MATERIAL
1. El movimiento
Hay dos formas de enfocar el estudio del movimiento de los cuerpos:
Cinemática: el estudio se realiza prescindiendo de las causas que originan el
movimiento.
Dinámica: el estudio se realiza teniendo en cuenta estas causas.
1.1. Tipos de movimiento
Hay que distinguir dos tipos de movimiento.
Movimiento de traslación: si el cuerpo, considerado en conjunto como un
solo punto, cambia de posición, es decir, de localización respecto a otro
punto que consideramos como referencia.
Movimiento de rotación: el cuerpo gira en torno a un eje fijo, pero no se
desplaza.
Hay que tener en cuenta que reposo y movimiento son conceptos
relativos, pues dependen del objeto que tomemos como referencia. Por
ejemplo, mientras dormimos estamos en reposo respecto a la Tierra pero
en movimiento respecto al Sol. Así, cabe distinguir:
Movimiento absoluto: el punto de referencia se supone fijo respecto al
que se mueve.
Movimiento relativo: el punto cambia de posición respecto a otro que
también se mueve.
1.2. Elementos fundamentales del movimiento
El objeto móvil o punto material. Un cuerpo, por grande que sea, se
considera un punto material si sus dimensiones son despreciables
comparadas, bien con la distancia que hay entre él y el punto de
referencia, bien con la longitud de la trayectoria.
El sistema de referencia. El más simple consiste en un punto O (origen)
respecto al que referiremos el movimiento, junto con unos ejes de
coordenadas que nos servirán para localizar al punto material objeto de
estudio.
Si el punto O está en reposo o se mueve con velocidad constante,
hablamos de un sistema de referencia inercial.
La trayectoria. Es el lugar geométrico de las sucesivas posiciones que va
tomando el móvil en el espacio.
2. Magnitudes del movimiento
2.1. Posición
La posición de un punto P es su localización en el espacio. Se puede
localizar un punto en el espacio mediante tres coordenadas cartesianas
⃗⃗⃗⃗⃗ ), que une el origen del
P(x, y, z) y mediante un vector ⃗⃗
sistema de referencia con el punto P y se denomina vector de posición.
El vector de posición puede expresarse mediante como producto de su módulo
por un vector unitario (de módulo 1) que tenga su misma dirección y sentido:
| | ⃗⃗⃗⃗
Los vectores unitarios que tienen la misma dirección y sentido que los ejes
cartesianos se representan, respectivamente, como ⃗⃗⃗⃗ ) (⃗⃗⃗⃗ ) ⃗ ⃗⃗⃗⃗ ). De
este modo, todo vector puede descomponerse en sus componentes
cartesianas:
⃗
Cuando un punto P se mueve, su vector de posición cambia con el tiempo:
)
)
)
)⃗
Esta expresión se conoce como posición instantánea. Dando valores a t se
obtienen las distintas posiciones de la partícula móvil durante un intervalo de
tiempo, es decir, la trayectoria. Para calcular la distancia en cualquier instante
entre la partícula móvil y el sistema de referencia se calcula el módulo del
vector de posición.
)
√
Ejemplo:
El movimiento de una partícula viene dado por las ecuaciones x = 4t, y = 2t – 2,
con x, y en metro y t en segundos. Calcula:
a)
b)
c)
d)
La posición de la partícula en cualquier instante.
La posición en los instantes t = 0 y t = 2.
Posición de la partícula a los 5 s.
¿A qué distancia del origen se encuentra la partícula en ese instante?
Solución:
a)
)
b) Sustituyendo t por 0 y por 2 s obtenemos:
)
)
⃗
c) Procediendo igual que en el apartado anterior:
)
d) La distancia pedida será el módulo del vector posición:
)
√
2.2. Desplazamiento
Si en los instantes 1 y 2 los vectores de posición del móvil son
respectivamente, ⃗⃗⃗ ⃗⃗⃗ , el vector desplazamiento, , está dado por
⃗⃗⃗
⃗⃗⃗
En el ejemplo anterior, el desplazamiento del móvil entre los instantes
t = 0 y t = 2 será:
)
2.3. Espacio recorrido
Es el módulo del vector desplazamiento. En el ejemplo anterior:
√
2.4. Velocidad
La velocidad media es el desplazamiento que experimenta el punto móvil
en la unidad de tiempo. Es, por tanto, una magnitud vectorial.
Si el intervalo de tiempo tiende a cero, hablamos de la velocidad que tiene
el móvil en un instante o velocidad instantánea.
→
El módulo del vector velocidad (obviamente escalar) se denomina rapidez.
2.5. Aceleración
Es la variación de la velocidad por intervalo de tiempo.
Cabe distinguir:
Aceleración media:
⃗
Aceleración instantánea:
→
La velocidad puede variar tanto en módulo como en dirección, por lo que
habrá un tipo de aceleración relacionado cada una de estas variaciones.
Aceleración tangencial: Es debida a la variación de la rapidez o módulo de
la velocidad.
Aceleración normal: se debe al cambio de dirección de la velocidad, y
recibe el nombre de aceleración centrípeta.
Como puede observarse en la figura, Δv no es tangente a la trayectoria
como lo es el vector velocidad, sino que su dirección varía continuamente.
En cualquier caso, siempre puede descomponerse en un vector paralelo a
v1 u otro perpendicular al mismo. En otras palabras, hay una componente
de la aceleración tangente a la trayectoria y otra perpendicular (normal) a
la misma. Esta última componente es la que “obliga” al cuerpo a girar, y la
que se denomina aceleración centrípeta por estar dirigida siempre hacia el
centro de la trayectoria. Su módulo es:
Si elegimos el sistema de referencia formado por un punto de la
trayectoria y dos vectores unitarios, uno con la dirección de la tangente y
otro con la dirección normal (perpendicular) a dicha tangente, hemos
definido un sistema de referencia ligado a la propia trayectoria, que recibe
el nombre de sistema de referencia intrínseco a la trayectoria. Del mismo
modo, las aceleraciones tangencial y normal recién el nombre de
componentes intrínsecas de la aceleración.
3. Movimientos rectilíneos
La trayectoria es una línea recta. Por tanto, la dirección de la velocidad se mantiene
constante.
El mejor sistema de referencia es aquel que elige el origen O sobre la trayectoria, y
hace que ésta coincida con uno de los ejes cartesianos. De este modo, todas las
magnitudes del movimiento tienen la misma dirección del eje elegido y, por tanto, una
sola componente.
)
| |
)
| |
)
| |
)
| |
El módulo de estos vectores coincide con el de su única componente, y el sentido
puede expresarse con los signos +/-. Si el móvil no cambia el sentido del movimiento,
el módulo del desplazamiento coincide con el espacio recorrido.
3.1. Movimiento rectilíneo y uniforme (MRU)
La velocidad es constante. Por tanto, la velocidad media coincide con la
instantánea.
La ecuación del movimiento es
La gráfica velocidad-tiempo es una recta paralela al eje de tiempos:
Mientras que la gráfica espacio tiempo es una recta cuya pendiente
coincide con el valor de la velocidad.
3.2. Movimiento rectilíneo uniformemente acelerado (MRUA)
Se realiza con aceleración constante. Por tanto, la aceleración media y la
instantánea coinciden.
Sus ecuaciones son:
Obviamente, si la aceleración es negativa (la velocidad disminuye) los
signos + delante de la aceleración se sustituyen por signos -.
Eliminando el tiempo de las dos ecuaciones anteriores se obtiene:
)
La gráfica aceleración-tiempo es una recta paralela al eje de tiempos.
La gráfica velocidad-tiempo es una recta cuya pendiente nos da la
aceleración, si bien en este caso la pendiente puede ser negativa.
Por último, la gráfica espacio-tiempo es una rama de parábola, como
consecuencia de que, al variar la velocidad, se recorren espacios diferentes
en iguales intervalos de tiempo.
3.3. La caída libre
No es más que el movimiento de un cuerpo bajo la acción de la gravedad,
despreciando la resistencia del aire. Es un MRUA, de aceleración positiva si
el cuerpo bajo y negativa si sube. Las ecuaciones son las mismas que en el
caso general, sin más que cambiar “a” por “g = 9,8 m/s2”.
4. Movimiento circular
Ya los matemáticos griegos advirtieron que la relación entre la longitud de una
circunferencia y el diámetro de la misma era constante, un número al que llamaron π.
O bien, dado que el diámetro de la circunferencia es dos veces su radio:
⇒
Mucho después, se implantó como unidad SI de ángulo sólido el radián (rad), definido
de tal modo que el ángulo total de una circunferencia (360 o) equivale a 2π rad.
Por tanto, cuando describimos una circunferencia completa hemos recorrido un
ángulo de 2π rad; sin embargo, si extendiésemos la circunferencia formando un
segmento de recta, la longitud de éste dependería del radio de la circunferencia, de
acuerdo con la relación
En otras palabras, si tenemos dos circunferencias tales que el radio de la segunda sea
doble que el de la primera, al completar una vuelta habremos recorrido el mismo
ángulo en ambos casos (2π rad), pero para completar la revolución a la segunda
habremos recorrido una distancia doble.
Para un radio constante, la longitud del arco de circunferencia descrito es
directamente proporcional al ángulo recorrido, de tal modo que si la trayectoria
descrita cubre media circunferencia (π rad) la longitud recorrida será l/2. En general
teniendo en cuenta la relación entre el radio de la circunferencia y su perímetro, la
expresión general puede escribirse como
4.1. Movimiento circular uniforme
Si dividimos la expresión anterior por el tiempo, teniendo en cuenta que el
radio es constante:
⇒
Donde hemos definido la velocidad angular ω como
⁄
Cuya unidad SI es rad/s. A veces se usan otras unidades como
revoluciones/minuto (rpm), cuya conversión a rad/s se realiza:
Llamamos período (T) al tiempo necesario para completar una vuelta.
Dado que la longitud recorrida en una vuelta es 2πr, podemos definir la
velocidad lineal (constante y tangente a la trayectoria en todo punto)
como
⇒
La unidad SI de período es, obviamente, la de tiempo (s).
Del mismo modo, se define la frecuencia (número de vueltas en la unidad
de tiempo) como la inversa del período.
)
Cuya unidad SI es 1/s (s-1) o hercio (Hz).
En estos movimientos se conserva el módulo de la velocidad pero no su
dirección, que varía constantemente. Por tanto, existe una aceleración
centrípeta de valor
Sin esta aceleración centrípeta la partícula no describiría un movimiento
circular; y si en un determinado instante la aceleración centrípeta se
redujera a cero, la partícula seguiría un MRU en dirección de la tangente.
4.2. Coordenadas polares
En el estudio de los movimientos circulares, con frecuencia es preferible
usar un sistema de coordenadas distinto del cartesiano. Se trata del
sistema de coordenadas polares, en el que la posición del punto queda
definida por el radio de la circunferencia trayectoria y el ángulo que su
posición forma en cada instante forma con la horizontal, situando el origen
en el centro de la circunferencia trayectoria.
Las posiciones X e Y del móvil se obtienen proyectando el vector posición
sobre los correspondientes ejes.
De la figura inferior es fácil observar que:
√
)
√
√
Que es, precisamente, la ecuación de la circunferencia.
Podemos, por ejemplo, calcular la posición de un punto que describe un
movimiento circular de radio 2 metros cuando su vector de posición forma
un ángulo de 30o con la horizontal.
4.3. Movimiento circular uniformemente acelerado
En este caso la velocidad angular no es constante.
Si partimos de ⇒
y dividimos por el tiempo:
Donde hemos definido la aceleración angular α, cuya unidad SI es rad/s2.
Las ecuaciones de este movimiento son equivalentes a las del MRUA:
Dado que existen dos aceleraciones (tangencial y normal) perpendiculares
entre sí, la aceleración total se calcula usando el teorema de Pitágoras.
√
5. Composición de movimientos
La mayoría de los movimientos no se desarrollan en una dimensión sino en dos (en un
plano).
Por ejemplo, supongamos una pelota que rueda sobre una mesa sin rozamiento; el
movimiento se desarrolla en una sola dimensión. Pero al llegar al borde de la mesa
sigue una trayectoria parabólica, que ya fue observada por Galileo Galilei. Para
explicar por qué sucede este, empezaremos viendo el principio de superposición:
Si una partícula está sometida simultáneamente a varios movimientos elementales
independientes, el movimiento resultante se obtiene sumando vectorialmente tales
movimientos independientes.
Por tanto, cuando la pelota pierde contacto con la mesa está sometida a dos
movimientos perpendiculares. Por un lado, sigue un MRU a lo largo del eje de la mesa
(movimiento inicial), y por otro sufre una caída libre debido a la gravedad.
También siguen trayectorias parabólicas los objetos lanzados formando un cierto
ángulo con la horizontal, de modo que cabe distinguir, para los movimientos de
proyectiles, entre tiros horizontales y oblicuos. Empezaremos con los segundos (caso
general) para después particularizar a los primeros.
5.1. Tiro oblicuo
Un poco de trigonometría basta para observar que las componentes de la
velocidad inicial son:
Dado que a lo largo del eje X no actúa ningún tipo de aceleración, la velocidad
se mantendrá constante; esto es:
En cambio, a lo largo del eje Y actúa la aceleración de la gravedad, que se
opone al movimiento. Por tanto:
Siguiendo el mismo razonamiento, es fácil ver que
A partir de aquí, podemos hacer un breve estudio de las características del
movimiento.

Altura máxima
La condición para que se alcance la altura máxima es que se anule la
componente vertical de la velocidad, esto es, vy = 0.
Por tanto:
⇒
Sustituyendo este valor del tiempo que se tarda en alcanzar la altura
máxima en la expresión de y:

Alcance máximo
La condición para que el alcance sea máximo es que la altura sea 0,
esto es, y = 0.
Sustituyendo y por 0 en la ecuación correspondiente, nos queda:
Resolviendo
√
La solución que surge con el signo (-) es negativa, y carece de
significado físico.
Este valor del tiempo, sustituido en la expresión de x, nos da el alcance
xmax.
En todo caso, y dado que somos libres de elegir el origen de laturas,
podemos hacer y0 = 0 y simplificar las expresiones. En este caso, la
altura máxima será, simplemente
Mientras que la expresión del tiempo de caída nos queda:
√
Ahora la solución que surge del signo (-) es igual a 0, como por otra
parte parece de sentido común, y la solución positiva es
La sustitución de este valor de t en la expresión de x conduce a
Ahora bien, usando las expresiones del seno del ángulo suma y del
seno del ángulo diferencia:
)
)
Sumando estad dos expresiones:
⇒
Sustituyendo este resultado en la expresión de xmax:
El alcance será máximo cuando:
⇒
⇒
Y su valor será
5.2. Tiro horizontal
Es el caso, por ejemplo, de la pelota que rueda por la mesa y termina
cayendo por su borde.
En este caso, α = 0, lo que implica que cosα = 1 y senα=0.
Las velocidades iniciales serán:
Las velocidades a lo largo de ambos ejes serán:
Y las distancias recorridas en ambas direcciones
Las características del movimiento son ahora:
 Altura máxima
Recordando la expresión obtenida en el apartado anterior, vemos que

Que lógicamente será igual a o si situamos el origen de alturas en el
punto donde se inicia la caída.
Alcance máximo
Si tomamos y0 = 0, entonces cuando el proyectil toca el suelo se
encuentra a una altura –y, y de la ecuación de y llegamos a
√
⇒
Y el valor de x será
√
Si situamos el origen de alturas en el punto más bajo de la trayectoria,
esto es, y = 0, entonces nos queda
⇒
√
⁄ ⇒
√
⁄