mm mm
Anuncio

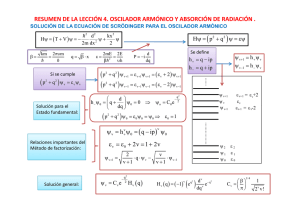
¿En qué condiciones se pueden analizar las oscilaciones de dos cuerpos como si fuera uno solo? ¿Qué magnitudes describen las oscilaciones de una molécula diatómica? ¿Qué parámetro sirve para comparar la rigidez del enlace molecular en una molécula diatómica? ¿Qué relación tiene el estudio de las oscilaciones de dos cuerpos con la espectroscopía infrarroja? A nivel microscópico, existen varias oscilaciones que se pueden aproximar con un movimiento armónico simple. En el caso de una molécula diatómica, se puede considerar como dos masas unidas por un resorte con constante de fuerza k. Este movimiento se puede considerar armónico simple cuando las oscilaciones son pequeñas alrededor de la posición de equilibrio: La energía potencial se aproxima a una parábola. La aceleración y la posición son opuestas en dirección en todo momento. http://www.cleonis.nl/physics/coupling_img/rotational_vibrational_coupling2.gif Resnick, Hslliday, Krane, “Física”, Volunen 1, 4ª Edición, CECSA, México, pg 355 http://physics-animations.com/Physics/English/mech.htm Una forma de analizar el movimiento de este sistema es x2 x1 analizando el movimiento de k cada una de las masas por 0 +F -F separado. Este análisis sólo es válido cuando el centro de masa no experimenta aceleración Sistema inercial Si L es la longitud del resorte sin estirar, el cambio en su longitud se puede expresar como: x x2 x1 L La fuerza ejercida sobre cada partícula es: F k x Si el resorte ejerce una fuerza –F sobre m2, entonces la fuerza sobre m1 es +F. Aplicando la segunda ley de Newton por separado tenemos: m2 x2 k x y m1 x1 k x Multiplicando la primera ecuación por m1 y la segunda por m2 y luego restando se obtiene: m1m2 x2 m1m2 x1 m1k x m2 k x La cual se reduce a: m1m2 d 2 x2 x1 k x 2 m1 m2 dt Definimos la masa reducida como: m1m2 m1 m2 Por lo tanto, la ecuación a resolver es: x k x 0 ¡¡¡Esta es la ecuación de movimiento del oscilador armónico simple!!! La frecuencia natural del oscilador es: 0 k En una molécula diatómica, lo que define el movimiento es la masa reducida y la separación relativa de los núcleos. La rigidez del enlace se puede estimar a partir del valor de la constante de fuerza de enlace k: Frecuencia Molécula x1013 Hz Constante de Fuerza N/m HF 12.4 970 HCl 8.66 480 HBr 7.68 410 HI 6.69 320 CO 6.42 1860 NO 5.63 1530 http://hyperphysics.phy-astr.gsu.edu/hbase/molecule/vibspe.html#c1 Para observar gráficamente: http://users.hartwick.edu/hartleyc/springs/springs.html Los diferentes modos de vibración de un mismo compuesto tienen una frecuencia característica cada uno. El análisis de las frecuencias de vibración permite la identificación de un compuesto Espectroscopía de absorción infrarroja (IR). Las masas reducidas ocasionadas por la presencia de diferentes isótopos ocasionan variaciones en las frecuencias de vibración de un mismo compuesto. http://www.phy.davidson.edu/stuhome/sethvc/laser-final/co2.htm http://science.widener.edu/svb/ftir/ir_co2.html 4. Asumiendo que la vibración de una molécula de HCl puede considerarse como un oscilador armónico, calcule: (1 u.m.a. =1.66 x 10-27 kg) a) ¿Cuál es la masa reducida del HCl? b) En un experimento se mide la frecuencia de vibración como se muestra en la figura. ¿Cuál sería la constante de fuerza del oscilador correspondiente? http://hyperphysics.phy-astr.gsu.edu/hbase/molecule/vibrot.html#c1 5. Por medio de cálculos de mecánica cuántica se obtiene que la constante de fuerza del oscilador correspondiente a las vibraciones del HBr es 410 N/m. a) ¿Cuál es la frecuencia natural de este oscilador? b) En general, los espectros de IR se miden en números de onda entre 400 y 4000 cm-1. ¿Cuál sería la frecuencia de vibración de la molécula en cm-1? ¿Y en eV? http://hyperphysics.phyastr.gsu.edu/hbase/molecule/ vibrot3.html#c1