Anarmonicidad y Resonancia en Vibraciones de Moléculas
Anuncio

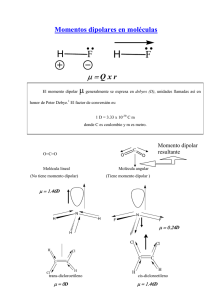
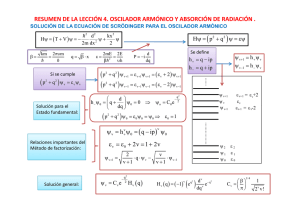
Anarmonicidad y Resonancia en Vibraciones de Moléculas Estructura de la materia. Profesor: Luis Alberto Vicente Hinestroza Laura Morales Toledo Víctor Augusto Moreno Martínez 20 de Marzo del 2014 Jaime Arturo Pérez Reséndiz Introducción Probabilidad de transición Cuando la radiación electromagnética atraviesa un sistema de partículas cargadas, como el que forman los electrones y núcleos constituyentes de átomos y moléculas, los campos eléctrico y magnético de la radiación interactúan con las cargas provocando una perturbación dependiente del tiempo que puede inducir transiciones entre los diferentes estados cuánticos del sistema. El objetivo es determinar cuál es la probabilidad de que se produzcan estas transiciones. Sea el operador Hamiltoniano de un determinado átomo o molécula. Este Hamiltoniano no depende, en general, del tiempo, y su ecuación de valores propios viene dada por donde y son las funciones propias y valores propios de la energía. La radiación electromagnética provoca una perturbación dependiente del tiempo cuyo Hamiltoniano de interacción se puede escribir, en general, de la forma . El Hamiltoniano completo se puede escribir: Suponiendo que el átomo esta inicialmente en el estado estacionario . Bajo el efecto de la perturbación la función de onda evoluciona con el tiempo a partir de dicho estado inicial, y existe cierta probabilidad de que, después de aplicar la radiación, el átomo se encuentre en un estado estacionario final diferente probabilidad de transición estado estacionario final . Se obtiene, pues, la para transitar del estado estacionario . Partiendo de la ecuación de Schrödinger dependiente del tiempo Sustituyendo el operador Hamiltoniano total de se obtiene al Se expresa como una combinación lineal de los estados estacionarios del sistema sin perturbar donde los coeficientes es decir varían con el tiempo, Sustituyendo la en la se tiene y desarrollando los términos a ambos lados del igual queda en el primer término a la derecha del signo igual se uso la ., este término es idéntico al segundo término a la izquierda del signo igual, ambos se cancelan y se obtiene Multiplicando por la izquierda por la conjugada compleja de alguna función propia del sistema de orden cero, , e integrando sobre todo el espacio, obtenemos el siguiente sistema de ecuaciones diferenciales acopladas para los coeficientes , donde y Hasta este punto no se ha hecho ninguna aproximación, así que el sistema de ecuaciones diferenciales es completamente equivalente a la ecuación de Schrödinger dependiente del tiempo. Como se ha indicado antes, suponiendo que el sistema está inicialmente en el estado estacionario , es decir que a tiempo se cumple Esto implica que los valores iniciales de los coeficientes del desarrollo de onda valen para la función Si la perturbación es suficientemente pequeña, cabe esperar que los coeficientes cambien muy poco con respecto a sus valores iniciales. Para facilitar la resolución del sistema de ecuaciones , podemos aproximar los coeficientes que aparecen en las mismas al lado derecho del signo igual por sus valores iniciales. El sistema de ecuaciones se simplifica como sigue Esto equivale a realizar un tratamiento perturbativo de primer orden de la ecuación de Schrödinger dependiente del tiempo. Integrando las ecuaciones obtenemos y para tiene , es decir para coeficientes distintos del correspondiente al estado inicial, se y la ecuación anterior se reduce a La probabilidad de transición función propia en el desarrollo , viene dada por el cuadrado que multiplica a la , o sea Sustituyen aquí la expresión para obtenemos finalmente Reglas de selección Obtenidos los niveles de energía y las funciones de onda de vibración y rotación de las molecular diatómicas, se puede pasar a determinar las reglas de selección que controlan las transiciones radiativas entre estos niveles. Las reglas de selección más fuertes son las de dipolo eléctrico y se obtienen calculando el momento dipolar de transición eléctrico. En el marco de la separación de BornOppenheimer, las funciones de onda moleculares vienen dadas por el producto de la función de onda electrónica y la nuclear, es decir Para las transiciones entre dos estados moleculares y , en las que el estado electrónico no cambia ( ), es decir, para transiciones dentro de la misma curva de energía potencial, el momento dipolar de transición viene dado por Donde el operador momento dipolar es: Por lo que la ecuación puede reescribirse (2) como: donde la integral entre corchetes es el valor esperado del operador momento dipolar en el estado electrónico . Este valor esperado, que depende de las coordenadas nucleares puesto que la integración se realiza sobre coordenadas electrónicas, es el momento dipolar eléctrico permanente de la molécula, , es decir: La simetría de la nube electrónica de la molécula diatómica hace que el vector momento dipolar eléctrico permanente este alineado con eje internuclear. Los vectores y tienen, por tanto, la misma dirección, de modo que están caracterizados por los mismos ángulos polares, y, y difieren únicamente en su longitud o módulo. Usando, coordenadas polares se escribe: donde se indica explícitamente que el módulo separación internuclear . depende únicamente de la Las funciones de onda nucleares de las moléculas diatómicas vienen dadas por el producto de las funciones de onda traslacionales por las funciones de onda internas . Desarrollando la integral de donde se ha tenido en cuenta que las funciones de onda traslacionales no cambian en la transición y que están normalizadas. Sustituyendo aquí la expresión de para el momento dipolar eléctrico permanente se obtiene: Sabiendo que las funciones de onda internas vienen dadas, además, por el producto de los armónicos esféricos por las funciones radiales, es decir , de modo que la integral anterior queda finalmente resuelta como: Donde se supone que las funciones radiales no dependen del número cuántico rotacional, lo que equivale a utilizar el modelo del rotor rígido. Evaluando las integrales que aparecen en la expresión anterior. Las integrales angulares son las mismas que se resuelven para determinar las reglas de selección del átomo de hidrogeno, así que las reglas de selección de los números cuánticos rotacionales son: Para evaluar la integral radial de la 26 se necesita saber cómo varia el modulo del momento dipolar eléctrico permanente , con la distancia internuclear . Suponiendo primero que la molécula diatómica es heteronuclear. En este caso no hay separación neta de carga electrónicas puesto que los núcleos son iguales. El momento dipolar eléctrico permanente de la molécula es nulo y de acuerdo con la 26 se anula también el momento dipolar de transición . Las transiciones de dipolo eléctrico entre niveles de energía de vibración y rotación de moléculas diatómicas homonucleares están prohibidas y estas moléculas no presentan por tanto, espectro de vibración-rotación. Con las moléculas diatómicas heteronucleares hay separación neta de carga con respecto a los núcleos, por lo que el momento dipolar eléctrico permanente es diferente de cero . Para averiguar cómo cambia el modulo de este vector con la distancia internuclear , se evalúa la integral electrónica de la 24. Se puede ver, como varía cualitativamente realizando consideraciones físicas. Así, para , los dos átomos de la molécula están unidos formando un solo átomo más pesado y puesto que un atomo no tiene un momento dipolar eléctrico neto, entonces En el otro extremo, a separación infinita, los átomos no interactúan como generalmente las moléculas diatómicas disocian en sus átomos neutros, en lugar de hacerlo en sus iones, se tiene que . El momento dipolar debe aumentar pues desde cero, en el límite de átomos unidos , pasar por un máximo a una distancia internuclear dada, que habitualmente es mayor que y volver a después a disminuir asintóticamente hacia cero a medida que la separación internuclear tiende a infinito, tal como se muestra en la figura 1. Figura 1. Variación del módulo del momento dipolar eléctrico permanente con la distancia internuclear. Suponiendo que se expresa el modulo del momento dipolar permanente ( ) como un desarrollo en serie de Taylor de la distancia internuclear en torno a su valor de equilibrio . Por lo que se tiene: Donde la primera derivada del momento dipolar permanente es, en general, diferente de cero puesto que la distancia de equilibrio de la molécula no coincide, en general, con el máximo del momento dipolar permanente figura 1. Si nos quedamos con los primeros dos términos el desarrollo , es decir, si usamos una aproximación lineal para el momento dipolar eléctrico permanente, y la sustituimos en la ecuación integral radial (9) se tiene que: Donde se ha usado la variable radial de desplazamiento y se ha sustituido el límite inferior de integración, que debe de ser - , por - ya que el intervalo que va desde - hasta - las funciones de onda radiales toman valores muy pequeños. La primera integral de la expresión es la integral de ortonormalidad de las funciones radiales , que se anula para y vale la unidad para . La regla de selección es por tanto , es decir, el numero cuántico vibracional no cambia. Solo cambia entonces el número cuántico rotacional de modo que las transiciones se producen entre estados con el mismo número cuántico vibracional ( y diferente número cuántico rotacional ( . Estas transiciones dan lugar al denominado espectro de rotación pura de la molécula. Para evaluar la segunda integral que aparece en la se supone la aproximación de las funciones como las del oscilador armónico. La integral toma entonces valores distintos de cero sólo cuando los números cuánticos vibracionales difieren en una unidad, es decir de manera que la regla de selección es . Ahora sí que cambia el número cuántico vibracional, además de los rotacionales, y las transiciones dan lugar al espectro de vibración-rotación de la molécula. Oscilador armónico Las oscilaciones armónicas ocurren cuando un sistema contiene un parte que experimenta una fuerza de restauración proporcional al desplazamiento de la posición de equilibrio. La energía potencial de una molécula diatómica incrementa si los núcleos están desplazados de sus posiciones de equilibrio. Cuando ese desplazamiento es pequeño, se puede expresar la energía potencial como los primeros términos de una serie de Taylor: donde el subíndice 0 indica que las derivadas se evalúan en la longitud de enlace de equilibrio . Al no ser de interés en el valor absoluto de la energía potencial se puede establecer . A la distancia de equilibrio la primera derivada es cero, porque ahí la curva de energía potencial tiene un mínimo. Para desplazamientos pequeños los términos de más grandes que el de segundo orden pueden ser omitidos. El único término restante es el proporcional a , así se puede escribir La energía potencial cercana a la distancia de equilibrio es parabólica (es decir, proporcional a ), Se sigue que el Hamiltoniano para dos átomos de masas & es Cuando la energía potencial depende solamente de la separación entre las partículas del sistema, el Hamiltoniano puede ser expresado como una suma, un término refiriéndose al movimiento del centro de masa del sistema y el otro al movimiento relativo. El primer término no es de interés en el estudio de vibraciones moleculares y el segundo es donde es la masa efectiva (masa reducida): La aparición de en el Hamiltoniano es físicamente plausible, por que se espera que el movimiento este dominado por el átomo más ligero (en comparación con el otro átomo). Cuando , , la masa de la partícula más ligera. Pensando en una pequeña partícula unida por un resorte a una pared, es la masa de la partícula la que determina las características del sistema, no la masa de la pared. Un Hamiltoniano con una energía potencial parabólica es característica de un oscilador armónico, por lo que se puede adoptar las soluciones encontradas con . Estos niveles se encuentran en una escala informe con separación . Las correspondientes funciones de onda son una funciones gaussianas con forma de campana multiplicadas por un polinomio de Hermite. Anarmonicidad Las aproximaciones hechas para el oscilador armónico y el rotor rígido son solamente válidas para estados de vibración y rotación poco excitados, cercanos al fundamental. Las energías vibracionales y rotacionales de estos estados caen en la zona más baja de la función de energía potencial , que es la energía que mejor se aproxima mediante el oscilador armónico. Conforme va aumentando la energía potencial, los núcleos pasan más tiempo en las regiones alejadas del punto de equilibrio. En dichas regiones la energía potencial se desvía apreciablemente de la del oscilador armónico y la aproximación armónica por lo tanto, empeora, convirtiéndose en un oscilador anarmónico; su energía potencial cambia en forma periódica a medida que fluctúa la distancia entre las masas de los átomos sin embargo, desde un punto de vista cualitativo se trata de una descripción imperfecta de la vibración molecular. Por ejemplo, cuando dos átomos se acercan entre sí, la repulsión electrostática entre los dos núcleos produce una fuerza que actúa en la misma dirección que la fuerza restauradora del enlace. Por esta razón, puede esperarse que la energía potencial se eleve con más rapidez que la que predice la teoría del oscilador armónico. En lugar de estar equiespaciados los niveles vibracionales de una molécula diatómica, se van acercando más y más conforme aumenta y finalmente la energía vibracional se hace lo suficientemente grande como para provocar la disociación de la molécula diatómica en sus átomos que dejan de estar enlazados entre sí. La curva ideal del oscilador armónico cambia cuando toma la forma anarmónica que se muestra en la curva 2b de la figura 2. Estas curvas se apartan del comportamiento armónico en distintos grados, dependiendo de la naturaleza del enlace y de los átomos. Sin embargo, se observa que las curvas armónicas y anarmónicas son casi iguales para energías potenciales bajas. La oscilación anarmónica causa desviaciones de dos clases: a números cuánticos más altos, la diferencia de energía se hace menor (véase la curva 2b en la figura 2), y la regla de selección no se cumple con rigor. Como resultado, se observan algunas veces transiciones más débiles. Estas transiciones corresponden a . Si se utilizan funciones propias anarmónicas para entonces se obtiene que las transiciones con son permitidas, aunque su intensidad disminuye apreciablemente conforme aumenta . Se dice en este caso que las transiciones están permitidas debido a la anarmonicidad mecánica. Si se incluyen también términos superiores al lineal en el desarrollo en serie del momento dipolar eléctrico permanente, entonces aparecen integrales del tipo que tambien contribuyen al momento dipolar de transición y que refuerzan las reglas de selección con Se dice entonces que el oscilador posee anarmonicidad eléctrica. Ambas anarmonicidades, mecánica y eléctrica, son las responsables de las transiciones vibracionales con . De acuerdo con todo lo dicho, las reglas de selección vibracionales son las siguientes: Donde las variaciones del número cuántico vibracional entre paréntesis dan lugar a transiciones más débiles conforme aumenta . Figura 2. Diagramas de energía potencial. a) oscilador armónico b) curva de movimiento anarmónico. Las frecuencias de dichas transiciones de sobretono son aproximadamente del doble o triple de la frecuencia fundamental, y las intensidades son menores que la de la fundamental. Para describir estados más excitados se incluyen un número mayor de términos en los desarrollos de la serie de Taylor de la función de potencial y de la distorsión centrífuga. Los nuevos términos complican en general, resolver de forma analítica exacta la ecuación de Schrödinger radial, pero debido a que la magnitud de los mismos es pequeña se puede utilizar la teoría de perturbaciones para calcular las energías y funciones de onda de vibración y rotación. Debido a que no es posible resolver la expansión de Taylor de la energía potencial molecular para el oscilador anarmónico después del término cuadrático es sólo una aproximación, en moléculas reales los términos omitidos son importantes, particularmente para desplazamientos de equilibrio grandes. La curva típica de energía potencial se muestra en la figura 2a, debido a que a altas excitaciones se pierde la característica de parábola y como se dijo anteriormente, los niveles de energía se van acercando más en vez de estar uniformemente separados. Una manera de afrontar las anarmonicidades es resolver la ecuación de Schrödinger con el término de energía potencial que une la verdadera energía potencial en un mejor rango de valores para formar la parábola. Una de las funciones de aproximaciones más usadas es el potencial Morse, este modelo es más conveniente para calcular la energía potencial de una molécula diatómica, porque incluye los efectos de la ruptura de enlace, la anarmonicidad de los enlaces entre otras. Se plantea de la siguiente manera: El parámetro señala la profundidad del mínimo de la curva e indica la energía de disociación y , indica el desplazamiento del equilibrio. La ecuación de Schrödinger puede ser resuelta analíticamente con la energía potencial que se muestra a continuación, cuyos niveles de energía cuantizada son: La constante es llamada la constante de anarmonicidad. El término adicional se resta de la expresión armónica y se vuelve más importante a medida que crece, dando como resultado una convergencia en los niveles de alta excitación. Una característica de la energía potencial de Morse es que el número de niveles de enlace es finito: El modelo de oscilador Morse es sólo una aproximación para el modelo real del oscilador molecular. La forma de la solución sugiere que de los niveles de energía vibracional para tal sistema pueden aproximarse mediante la serie Las constantes espectroscópicas son mejor tratadas como parámetros obtenidos de adecuar la ecuación anterior a las transiciones espectrales experimentales. La corrección de anarmonicidad reduce la energía de cada nivel, pero la reducción es mayor para los niveles más altos. Por tanto, el espaciamiento entre niveles, , se reduce conforme aumenta. Para distinguir entre la anarmonicidad mecánica y eléctrica es necesario considerar que los efectos de la simetría no resuelven la aparición de transiciones para las que porque el polinomio de Hermite es simétrica. Los estados de de todos los modos normales son simétricas, y como el componente z del momento dipolar tiene especies simétricas es de esperarse que la transición 0 → 2 es permitida porque . Pero no debe olvidarse que la teoría de grupos es sólo válida cuando el valor de la integral es igual a 0, pero no cuando este valor es diferente de 0. En este caso con los sobretonos, cuando la componente en z del momento dipolo eléctrico tiene la forma de: El momento del dipolo eléctrico de transición del primer sobretono es Este elemento de la matriz es eliminado para el oscilador armónico. Sin embargo, cuando el sobretono se vuelve débilmente permitido para el oscilador armónico si hay presencia de anarmonicidad eléctrica, por lo que la cambia a: Y los términos de no son necesariamente igual a 0. La teoría e grupos no dice exactamente donde termina la serie e Taylor sólo que toma en cuenta una visión global de la simetría. La tiene términos cruzados correspondientes a con . Estos términos pueden dar lugar a bandas de combinación en el que más de un modo es excitado al mismo tiempo. Para determinar si la transición puede ocurrir en realidad, se debe de tomar en cuenta lo siguiente en el momento de transición dipolar eléctrica para la transición de A→B Existen dos contribuciones iguales de la forma y los primeros dos términos son cero en la ortogonalidad de los estados vibracionales. Sin embargo, la tercera no es necesariamente cero por lo que puede producirse la banda de combinación. Las bandas de combinación también son observadas como resultado de la anarmonicidad mecánica. En una molécula poliatómica la energía potencial sufre una variación en el desplazamiento La presencia del término cúbico quita la independencia de los modos normales porque la transformación que separa al Hamiltoniano con el término cuadrático no separa simultáneamente los términos restantes de la expansión. Un tipo de relaciones causadas por la anarmonicidad donde la interacción es entre el estado fundamental y la combinación de sobretono es la llamada Resonancia de Fermi. Resonancia de fermi en espectros El fenómeno de resonancia, en términos de física clásica, se considera que todo cuerpo o sistema tiene una, o varias, frecuencias características, las cuales dependen mucho de la elasticidad del objeto o sistema en sí o de la forma que este tiene. Cuando un sistema es excitado a una de sus frecuencias características, su vibración es la máxima posible. El fenómeno de resonancia se produce cuando la frecuencia angular de la fuerza externa coincide con la frecuencia natural de oscilación del sistema. En términos cuánticos el fenómeno de resonancia se considera cuando el estado fundamental de un sistema físico es doblemente degenerado (y suficientemente alejado del resto de los otros niveles), cualquier acoplamiento entre los estados correspondientes disminuye la energía del estado fundamental del sistema, el cual se convierte en más estable. La resonancia de Fermi es, un efecto anarmónico especialmente fuerte, que se da entre niveles de combinación, o sobretono, y niveles fundamentales con frecuencias muy próximas, la "resonancia de Fermi" aparece cuando un sobretono o una banda de combinación poseen una energía cercana a una vibración fundamental. Fig. 3 La banda de combinación (b,c) toma la intensidad del estado permitido (a) fundamental Espectros de rotación pura. Sabiendo que los espectros de rotación pura, que son aquellos en los que no cambia el número cuántico vibracional La regla de selección rotacional es . En una transición de absorción entre dos estados rotacionales con números cuánticos inicial y final , respectivamente, se obtiene, usando la ecuación proporciona los niveles de energía de vibración y rotación para los números de ondas de las líneas espectrales: Suponiendo en primer lugar que las constantes y son despreciables frente a la constante , es decir, que usamos la aprocimación del rotor rígido. Por lo que ahora se obtiene una nueva ecuación: Y el espectro rotacional consiste en una serie de líneas espectrales que aparecen en los números de inda , y que están, por tanto, equiespaciadas (Figura Siguiente). Los valores son normalmente del orden de varios cm-1, salvo para moléculas muy ligeras para las que pueden llegar a alcanzar las decenas de cm-1. (Sabiendo que es inversamente proporcional a la masa reducida de la molécula). De acuerdo con estos valores, los espectros de rotación pura se observan en habitualmente en la región de microondas, que van aproximadamente desde 0.03 hasta 10 cm-1 (1 a 300 GHz) y se extienden hacia el infrarrojo lejano. Fig. 4 Formación del espectro de rotación pura de una molécula diatómica. En la figura siguiente se muestra como ejemplo, el espectro de absorción rotacional de la molécula de CO ( =1.93cm-1) en la región del infrarrojo lejano, en la que entran las líneas espectrales con mayor que 3. A la izquierda de cada línea aparece un pequeño pico correspondiente a las frecuencias rotacionales de las especies isotópicas 13C16O y 12C18O. Estas líneas son mucho más débiles debido a la abundancia de estos isotopos. Fig. 5 Espectro rotacional de absorción de la molécula de CO Espectros de vibración-rotación Los espectros aparecen por convención al utilizad modelos del oscilador armónico y rotor rígido. Las reglas de selección son y los niveles de energía, en cm-1, viene dados por: Supongamos que el espectro es de absorción. El numero cuántico vibracional v aumenta en este caso, en una unidad , pero el número cuántico rotacional puede aumentar o disminuir , también en una unidad, y los números de ondas correspondientes a estos dos tipos de transiciones vienen dados por: El espectro de vibración-rotación se genera entonces de la forma que se muestra a continuación: Fig. 6 Formación del espectro de vibración-rotación de una molécula diatómica. El espectro aparece centrado en el número de ondas y sus líneas se sitúan a ambos lados del mismo dependiendo de que el numero cuántico aumente en la transición lo que da lugar a la denominada rama R del espectro, o que J disminuya en la transición , lo que origina la rama Las líneas de cada rama se denotan de la forma , donde es el número cuántico rotacional del estado de energía más baja. El espaciado entre las líneas en ambas ramas es constante e igual a la diferencia entre las primeras líneas de cada rama, es igual a . En medio de ellas está el número de ondas , en el lugar en el que debería de aparecer la línea espectral de vibración pura ( para ), si esta transición estuviese permitida. Esta es la posición del centro u origen de la banda. Los valores de la cte. Espectroscópica armónica van desde los 100cm-1 hasta los 4000cm-1, por lo que los espectros de vibración-rotación de moléculas diatómicas aparecen en la región del infrarrojo, que se extiende desde los 10cm-1 hasta, aproximadamente los 13000cm-1. A continuación se muestra el espectro de vibración-rotación de la molécula de CO en fase gaseosa, con sus ramas R y P perfectamente resueltas. Fig. 7 Banda de vibración-rotación de la molécula de CO. Fig. 8 Banda de vibración-rotación de la molécula de HCl. Los espectros de rotación-vibración se causan cuando las ondas electromagnéticas incidentes, siempre que tengan un momento dipolar eléctrico, excitan los niveles de rotación de las moléculas. El campo electromagnético ejerce un par de fuerza sobre la molécula. Los espectros de las transiciones rotacionales de las moléculas están típicamente en la región de microondas del espectro electromagnético. Se pueden obtener las energías de rotación de las moléculas rígidas con la ayuda de la ecuación Schrödinger. La molécula diatómica puede servir como ejemplo de cómo se pueden utilizar los determinados momentos de inercia, para calcular las longitudes de los enlaces. Fig. 9 Acción de un campo electromagnético a una molécula diatómica. La figura 10 muestra un poco de perspectiva sobre la naturaleza de las transiciones rotacionales. El diagrama muestra una parte del diagrama de potencial de un estado electrónico estable de una molécula diatómica. Ese estado electrónico tendrá varios estados vibracionales asociados con él, de modo que se pueden observar los espectros de vibración. Más común es observar las transiciones rotacionales que están asociadas con el estado de vibración fundamental. Fig. 10 Potencial de un estado electrónico estable de una molécula diatómica. Resonancia en espectros. IR Y RAMAN Raman e infrarrojo son técnicas complementarias al momento de estudiar las frecuencias vibracionales de una molécula, ya que ciertas frecuencias pueden ser observadas en IR mientras que en Raman son ausentes y viceversa. Raman tiene gran interés para el estudio de sustancias en disolución acuosa (medios biológicos) ya que el agua absorbe fuertemente en el IR, obstruyendo a otras bandas, pero no en el Raman. Por otra parte, es difícil técnicamente obtener espectros IR por debajo de 100cm-1. En Raman, la frecuencia fundamental (v0) no está relacionada con la diferencia de niveles y, de hecho, generalmente cae en el visible o ultra-violeta cercano. Por ello no existe problema en observar desplazamientos de Raman menores de 100cm-1 y hasta 10cm-1. El efecto de resonancia de Fermi, en IR, por lo general conduce a dos bandas que aparecen muy juntas cuando sólo se espera una. Cuando un armónico o una banda de combinación tiene la misma frecuencia que, o una frecuencia similar a, aparecen unos fundamentales, dos bandas las cuales dividen cada lado del valor esperado y son de aproximadamente la misma intensidad. El efecto es mayor cuando las frecuencias son iguales, pero también está presente cuando hay una falta de coincidencia de unas pocas decenas de números de onda. Las dos bandas se denominan como un doblete de Fermi. Sobretonos y bandas de combinación pueden a veces dar lugar a bandas inusualmente fuertes en los espectros de IR y Raman, compartiendo su identidad con una banda fundamental cercana de la misma simetría. Fig. 11 Resonancia de fermi en el espectro Raman de CO2. En la imagen superior se demuestra la influencia de la Resonancia de Fermi en el espectro Raman del CO2, para el cual se esperaría una única banda fundamental v1 debida a la vibración de una tensión simétrica. En su lugar, se observan dos bandas intensas a 1285 y 1388cm-1. Pero la vibración de flexión fundamental v2 está a 667cm-1 y su segundo sobretono debería aparecer cerca de 1334cm-1; estos componentes del sobretono se mezclan con la banda fundamental v1 dando lugar a dos bandas de intensidad similar, cada una formada aproximadamente 50% sobretono, 50% fundamental. Ejemplos de resonancia de fermi IR Cetonas Región carbonílica del espectro IR de la ciclopentanona (A) y la ciclopentanona perdeuterada (B). En A la resonancia de Fermi entre la vibración carbonílica y la vibración de combinación (ωCH2 + δC=O) genera el doblete observado. En B el alejamiento de la frecuencia de la banda de combinación de la frecuencia carbonílica elimina la RF. La RF es en la mayoría de los casos un efecto perturbador en la interpretación de los espectros IR. Fig. 12 Espectro de infrarrojo para ciclopentanona (A) y la ciclopentanona perdeuterada (B) Aldehídos En la mayoría de los aldehídos se presenta la ya mencionada Resonancia de Fermi mediante el acoplamiento del estado fundamental con el armónico del doblaje C-H. El fundamental del doblaje del hidrogeno en el plano C-H se encuentra en la mayoría de los aldehídos cerca de 1390cm-1 por lo que su armónico 2 C-H casi coincide en frecuencia con el fundamental de la vibración de valencia C-H (2800 cm-1). El acoplamiento de osciladores produce dos vibraciones híbridas, que comparten características, entre ellas la intensidad. Se produce el llamado doblete de Fermi: Dos bandas de intensidad media cerca de 2800 y 2700cm-1, que caracteriza a la mayoría de los espectros IR de los aldehídos y permite su diferenciación de las cetonas. Fig. 13 Espectro de infrarrojo para benzaldehído Bibliografía. Atkins, P., Friedman, R., Molecular Quantum Mechanics, 4ª Edition, U.S.A., (2005). Castellan, G. W., Fisicoquímica, 2a Edición, E.U.A, (1987). Requena A, Zúñiga, Espectroscopía, España (2004). Skoog, D.A., Foller, F. J., Principios de Análisis Instrumental, 6a Edición, E.U.A. (2008). Stuart, B., Infrared Spectroscopy: Fundamentals and aplications, Australia, (2004). [http://hyperphysics.phy-astr.gsu.edu/hbasees/molecule/vibrot.html#c1 marzo 2014] [Última consulta 6