FIS 231 Guía de ejercicios N° 8 Segundo Semestre 2012

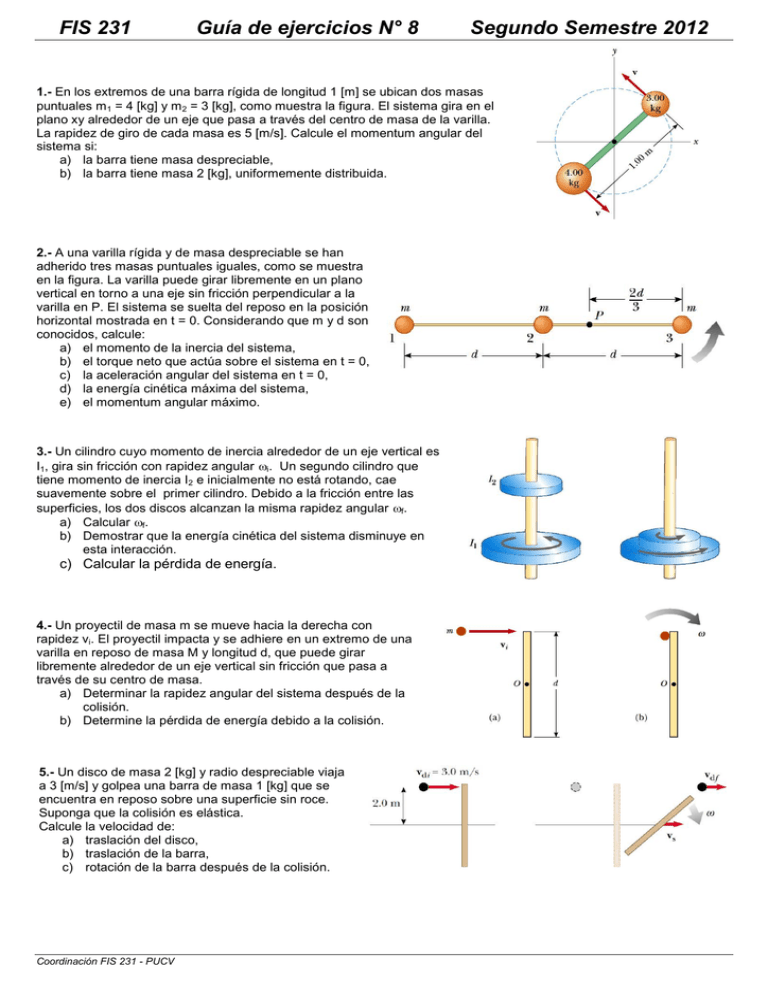
FIS 231
Guía de ejercicios N° 8
Segundo Semestre 2012
1.- En los extremos de una barra rígida de longitud 1 [m] se ubican dos masas
puntuales m1 = 4 [kg] y m2 = 3 [kg], como muestra la figura. El sistema gira en el
plano xy alrededor de un eje que pasa a través del centro de masa de la varilla.
La rapidez de giro de cada masa es 5 [m/s]. Calcule el momentum angular del
sistema si:
a) la barra tiene masa despreciable,
b) la barra tiene masa 2 [kg], uniformemente distribuida.
2.- A una varilla rígida y de masa despreciable se han
adherido tres masas puntuales iguales, como se muestra
en la figura. La varilla puede girar libremente en un plano
vertical en torno a una eje sin fricción perpendicular a la
varilla en P. El sistema se suelta del reposo en la posición
horizontal mostrada en t = 0. Considerando que m y d son
conocidos, calcule:
a) el momento de la inercia del sistema,
b) el torque neto que actúa sobre el sistema en t = 0,
c) la aceleración angular del sistema en t = 0,
d) la energía cinética máxima del sistema,
e) el momentum angular máximo.
3.- Un cilindro cuyo momento de inercia alrededor de un eje vertical es
I1, gira sin fricción con rapidez angular i. Un segundo cilindro que
tiene momento de inercia I2 e inicialmente no está rotando, cae
suavemente sobre el primer cilindro. Debido a la fricción entre las
superficies, los dos discos alcanzan la misma rapidez angular f.
a) Calcular f.
b) Demostrar que la energía cinética del sistema disminuye en
esta interacción.
c) Calcular la pérdida de energía.
4.- Un proyectil de masa m se mueve hacia la derecha con
rapidez vi. El proyectil impacta y se adhiere en un extremo de una
varilla en reposo de masa M y longitud d, que puede girar
libremente alrededor de un eje vertical sin fricción que pasa a
través de su centro de masa.
a) Determinar la rapidez angular del sistema después de la
colisión.
b) Determine la pérdida de energía debido a la colisión.
5.- Un disco de masa 2 [kg] y radio despreciable viaja
a 3 [m/s] y golpea una barra de masa 1 [kg] que se
encuentra en reposo sobre una superficie sin roce.
Suponga que la colisión es elástica.
Calcule la velocidad de:
a) traslación del disco,
b) traslación de la barra,
c) rotación de la barra después de la colisión.
Coordinación FIS 231 - PUCV
6.- Un bloque de madera de masa M que descansa
sobre una superficie horizontal sin fricción está
conectado a una barra rígida de longitud  y masa
despreciable que está pivoteada en el extremo
opuesto. Una bala de masa m que se desplaza en
forma paralela a la superficie horizontal y
perpendicular a la barra con rapidez v, golpea el
bloque y se incrusta en él.
a) Calcule el momento angular de sistema
bloque-bala.
b) ¿Qué fracción de la energía cinética original
se ha perdido en la colisión?
7.- Una bolita de plasticina de masa m y rapidez vi es
disparada contra un cilindro sólido de masa M y
radio R. El cilindro está inicialmente en reposo y
montado en un fijo eje horizontal que pasa por el
centro de masa. La línea de movimiento del proyectil
es perpendicular al eje del cilindro, y está a una
distancia d < R del centro.
a) Determinar la rapidez angular del sistema
justo después que la bolita se adhiere a la
superficie del cilindro.
b) ¿Se conserva la energía mecánica en este
proceso? Explique su respuesta.
8.- Un disco de masa de 80 [gr] y radio 4 [cm] se
desliza por una mesa de aire a una velocidad de
1,50 [m/s] como muestra la figura (a), chocando
tangencialmente con un segundo disco de radio 6
[cm] y masa 120 [gr]. Después del choque, los
discos se unen y giran en conjunto como muestra la
figura (b).
a) Calcule el momento angular del sistema
respecto del centro de masa después del
choque.
b) Calcule la rapidez angular de giro del
sistema alrededor del centro de masa.
c) Calcule la pérdida de energía en la colisión.
Coordinación FIS 231 - PUCV