TEMA 7 TRANSISTORES DE EFECTO CAMPO

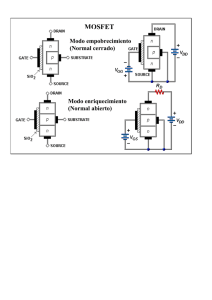
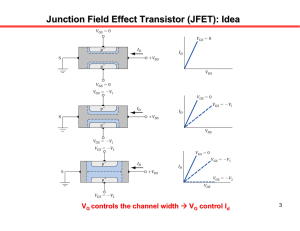
TEMA 7
TRANSISTORES DE EFECTO CAMPO
(Guía de Clases)
Asignatura: Dispositivos Electrónicos I
Dpto. Tecnología Electrónica
CONTENIDO
INTRODUCCIÓN
JFET: CURVAS CARACTERÍSTICAS
Símbolos de los JFET
Esquema básico de polarización
Curvas características
ZONAS DE FUNCIONAMIENTO
Región óhmica
Región de contracción
Región de saturación
Región de corte
Región de ruptura
EL TRANSISTOR MOS: ESTRUCTURA Y TIPOS
CURVAS CARACTERÍSTICAS
SÍMBOLOS GRÁFICOS
EL MOS EN CONMUTACIÓN
INVERSORES MOS Y CMOS
Transistores de efecto campo. Guía de clases
pg. 1
INTRODUCCIÓN
Transistor de efecto de campo (FET) son dispositivos semiconductores donde el control de la corriente se
realiza mediante un campo eléctrico. Tienen las siguientes características:
-
Dispositivo unipolar: un único tipo de portadores de carga
-
Ocupa menos espacio en un circuito integrado que el bipolar, lo que supone una gran ventaja
para aplicaciones de microelectrónica
-
Tienen una gran impedancia de entrada (del orden de MΩ)
Existen dos tipos de transistores de efecto campo:
-
De unión: JFET o simplemente FET
-
De puerta aislada: IGFET, MOS, MOST o MOSFET
Estructura de los JFET
-
Barra semiconductora con contactos óhmicos en los extremos
-
Puerta o elemento de control muy impurificado con portadores distintos a los de la barra
-
Elementos: Fuente o surtidor (S), Drenador (D), Puerta (G), y Canal (región situada entre las dos
difusiones de puerta
-
La tensión puerta surtidor (VGS) polariza inversamente las uniones
La corriente entre Drenador (D) y Fuente (S) se controla mediante el campo creado por la polarización
inversa aplicada a la puerta (G).
ANOTACIONES
pg. 2
Transistores de efecto campo. Guía de clases
JFET: CURVAS CARACTERÍSTICAS
Símbolos de los JFET:
D
D
G
G
S
S
Canal N
Canal P
Esquema básico de polarización:
+
IG
ID
+
VGG
VDS
VDD
IS
VGS
_
_
Para canal P el esquema es idéntico con polaridades invertidas
ANOTACIONES
Transistores de efecto campo. Guía de clases
pg. 3
Curvas características: ID = f (VDS, VGS)
Para VGS = 0:
•
VDS pequeña (<VP ): Canal casi completamente abierto => resistencia pequeña y aproximadamente
constante => comportamiento aproximadamente lineal => REGIÓN ÓHMICA
•
VDS cercana a VP : canal se va cerrando por un punto y la resistencia aumenta con la tensión =>
comportamiento no lineal => REGIÓN DE CONTRACCIÓN
•
VDS > VP : La resistencia rds es grande y aproximadamente constante => JFET fuente de corriente =>
REGIÓN DE SATURACIÓN
•
VDS muy elevada: Conducción inversa en las uniones, ID se dispara y se produce fácilmente la
destrucción del JFET => REGIÓN DE RUPTURA
ANOTACIONES
pg. 4
Transistores de efecto campo. Guía de clases
ZONAS DE FUNCIONAMIENTO
ÓHMICA: |VDS| < ||Vp| - |VGS||
ID
CONTRACCIÓN: |VDS| ≈ ||Vp| - |VGS||
SATURACIÓN: |VDS| > ||Vp| - |VGS||
VGS = 0
RUPTURA:
VDS elevada
|VGS|= |Vp|
CORTE: |VGS| > |Vp|
Región óhmica
|VDS| < | |Vp| – |VGS| |
Valores pequeños de VDS
Resistencia óhmica: rds =
L
1
q. N D . µ n 2ac
Valores usuales de la resistencia: de 100 Ω a 100 KΩ -> rds > Rcesat (transistor bipolar)
ID = f(VDS) -> función lineal
Cada VGS define un valor de resistencia distinto
ANOTACIONES
VDS
pg. 5
Transistores de efecto campo. Guía de clases
Región de contracción
|VDS| ≈ | |Vp| – |VGS| |
Al elevar VDS, ID deja de crecer linealmente -> se entra en la zona de contracción.
Cálculo de la tensión de contracción Vp
NA >> ND => wn ≈ w >> wp
w(x) = a – b(x) =
Vj = Vo + VI = (q ND w2)/(2ε)
2ε
(V + V ( x))
q. N D o
Si b = δ ≈ 0 (estrangulamiento) y Vo << V(x) entonces:
a=
q. N D 2
2ε
Vp ⇒ Vp =
a
2ε
q. N D
( )
Vp es la VDS que provoca estrangulamiento (estrechez máxima)
en un punto (para VGS=0) o la VGS que corta completamente el canal.
Si VDD = 0 => ID = 0 => Vo + V(x) = |VGS|, independiente de x
b⎞
2ε
2ε
⎛
2
VGS ⇒ ( a − b) =
VGS ⇒ VGS = ⎜ 1 − ⎟ V p
⎝
a⎠
q. N D
q. N D
2
a−b=
ANOTACIONES
pg. 6
Transistores de efecto campo. Guía de clases
Región de saturación
|VDS| > | |Vp| – |VGS| |
La anchura mínima del canal es δ. Al aumentar más la tensión entre drenador y fuente VDS, δ permanece
constante y aumenta L’ y se entra en la zona de saturación.
I DS
⎛
VGS
= I DSS ⎜ 1 −
⎜
Vp
⎝
⎞
⎟
⎟
⎠
2
;
siendo IDSS el valor de la corriente de saturación cuando la puerta está
cortocircuitada con la fuente (VGS = 0 )
Región de corte
|VGS| ≥ |Vp| => IDS ≈ 0
El canal desaparece
Región de ruptura
Cuando la tensión drenador fuente VDS es muy grande y entonces la corriente de drenador se eleva mucho y
se llega a la destrucción del FET.
ANOTACIONES
|VDS| ≥ BVDS
Transistores de efecto campo. Guía de clases
pg. 7
EL TRANSISTOR MOS. ESTRUCTURA Y TIPOS
Los transistores de efecto campo de unión JFET estudiados hasta ahora presentan la característica de que
con VGS = 0, ID no es nula cuando VDS ≠ 0.
Los transistores de efecto campo de puerta aislada (de acumulación) tienen ID nula con VGS = 0, lo cual es
interesante para trabajar en conmutación. Estos transistores de efecto campo de puerta aislada se suelen
llamar MOS (Metal Oxide Sc) y tienen una impedancia de entrada elevada, del orden de 1010 ÷ 1015 Ω
MOSFET de acumulación de canal P
Tipos:
-
Canal P -> sustrato N; impurificaciones P+
-
Canal N -> sustrato P; impurificaciones N+
Construcción de la zona del canal
-
Muy impurificada o enriquecida (enhacement) en los portadores de carga del sustrato -> MOS de
enriquecimiento o acumulación
-
Poco impurificada o empobrecida (depletion) en los portadores de carga del sustrato (enriquecida en los
portadores de las impurificaciones de D y S) -> MOS de empobrecimiento o de deplexión
ANOTACIONES
pg. 8
Transistores de efecto campo. Guía de clases
Curvas de salida: ID = f(VDS, VGS)
MOS de acumulación
Región de no saturación u óhmica: |VDS| < |VGS - VTH|
|ID|
Región de contracción: |VDS| ≈ |VGS - VTH|
Región de saturación: |VDS| > |VGS - VTH|
|VGS|
|VDS|
|BV|
Región de corte: |VGS| < |VTH|
Tensión de ruptura
ANOTACIONES
pg. 9
Transistores de efecto campo. Guía de clases
CURVAS CARACTERÍSTICAS
Es la representación de la corriente de drenador ID en función de la tensión entre la puerta y la fuente VGS
ID = f(VGS)
Con VDS constante se varía VGS y se observa ID , obteniéndose curvas diferentes para cada tipo de transistor:
Transistores enriquecidos (enhacement)
CANAL N
CANAL P
ID
VTH
ID
VGS
VGS
VTH
|ID| = K (|VGS| - |VTH|)2
K = 0’3 mA/V2
para |VGS| > |VTH|
Transistores empobrecidos (depletion)
CANAL P
CANAL N
ID
ID
Vp
IDSS
IDSS
VGS
-Vp
ID = IDSS(1 - VGS/ Vp)2
ANOTACIONES
VGS
pg. 10
Transistores de efecto campo. Guía de clases
SÍMBOLOS GRÁFICOS
Canal P
Canal N
D
D
EMPOBRECIDOS O
DE DEPLEXIÓN
(DEPLETION)
G
G
S
D
G
S
S
D
ENRIQUECIDOS O
DE ACUMULACIÓN
(ENHACEMENT)
G
S
Otro tipo de símbolo:
D
D
DEPLEXIÓN
G
G
S
S
D
D
ACUMULACIÓN
G
G
S
S
En electrónica digital:
D
D
ACUMULACIÓN
G
G
S
ANOTACIONES
S
pg. 11
Transistores de efecto campo. Guía de clases
EL MOS EN CONMUTACIÓN
Se usa el transistor de acumulación. RL ocupa aproximadamente veinte veces más área en un circuito
integrado que el transistor.
Recta de carga: VDD = IDRL + VDS
+VDD
RL
+
D
G
Vsal
+
Vent
S
_
_
ID
VGS = VDD
B
V’’’GS > V’’GS
V’’GS > V’GS
V’GS > VTH
VGS = VTH
≈0
Vent
Vsalida
0
+VDD
≈0
+VDD
ANOTACIONES
A +VDD
-> En lógica digital ->
Vent
Vsalida
punto A
0
1
punto B
1
0
VDS
pg. 12
Transistores de efecto campo. Guía de clases
El circuito anterior es un inversor. Símbolos del inversor:
1
INVERSORES MOS Y CMOS
-VDD
+
Q2
VL = VDS2 = VGS2
_
INVERSOR CON TRANSISTOR DE CARGA
CON PUERTA UNIDA A DRENADOR
+
Q1
Vsal = VDS1
+
Vent = VGS1
_
_
Q2 actúa como la resistencia de carga y se llama FET de carga. Q2 está siempre en saturación
independientemente de Q1 => Q2 tiene siempre el canal formado.
ANOTACIONES
pg. 13
Transistores de efecto campo. Guía de clases
ID2
VGS2 = -VDD
Lugar geométrico
donde VGS2 = VDS2
VGS2 = -VTH
VDS2 = VGS2
-VDD
-VTH
ID1 = ID2
VGS1 = -VDD
B
A
VON
-VDD + VTH
VGS1 = -VTH
VDS1 = -VDD - VDS2
-VDD
Curva de carga: ID1 = f(VDS1) = f(-VDD – VDS2)
Vent
Vsalida
-> En lógica digital ->
0
-VDD + VTH
punto A
0
1
-VDD
- VON
punto B
1
0
ANOTACIONES
Vent
Vsalida
pg. 14
Transistores de efecto campo. Guía de clases
-VDD
Q2
INVERSOR CON MOS DIFERENTES
(ACUMULACIÓN Y DEPLEXIÓN)
+
Q1
Vsal = VDS1
+
Vent = VGS1
_
_
VDD
S2
G2
Q2 (PMOS)
D2
INVERSOR CMOS
(MOS DE SIMETRÍA COMPLEMENTARIA)
+
+
D1
G1
Vent
Q1 (NMOS)
Vsal
S1
_
_
a) Vent = 0 => Q1 está en corte y Q2 en estado de conducción
VGS1 < VT y |VGS2| > |VT| => Vsal ≈ VDD
b) Vent = VDD => Q1 en estado de conducción y Q2 en corte
VGS1 > VT y |VGS2| < |VT| => Vsal ≈ 0
ANOTACIONES