1 Las operaciones financieras, las tasas y la doctrina judicial Cra
Anuncio

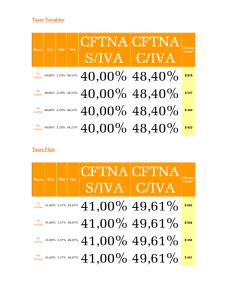
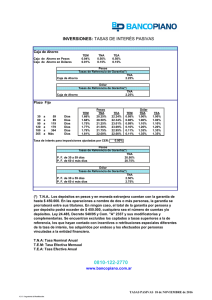
Las operaciones financieras, las tasas y la doctrina judicial Cra. Silvia E. Bertani 1. Introducción Una operación financiera se puede definir como: “todo cambio no simultáneo de dos o más capitales estipulado en un contrato, verbal o escrito, entre personas o entidades”. Toda operación financiera consta de 3 componentes fundamentales: Capital Tiempo Tasa La existencia de este último componente es resultado de un desfasaje en el tiempo del flujo de fondos. Este factor es fundamental para que exista una operación financiera, habida cuenta que “una unidad monetaria hoy no es lo mismo que una unidad monetaria mañana”. La sola existencia de capital no implica que se esté en presencia de una operación financiera. 2. Tasas activas y pasivas La tasa pasiva es la que abonan las Entidades Financieras por la captación de depósitos. La tasa activa es la que cobran las Entidades Financieras a los tomadores de fondos (deudores). La diferencia entre la tasa de interés pasiva y la activa se denomina "spread" La consideración de este tipo de tasas es tenida en cuenta en fallos judiciales, por ejemplo: Avan – Banco Tornquist: “Los intereses constituyen la contraprestación del deudor de una suma de dinero por el plazo que éste dispone para efectuar el pago del capital adeudado. El valor de mercado del dinero está dado por la tasa activa que es la que deberá pagar si pretende hacerse de dinero a su "real" precio en plaza.” El cómputo de los accesorios se efectuará según la tasa activa que emplea el Banco Nación en sus operaciones ordinarias de descuento a treinta días, (C.N.Com. en pleno in re SA La Razón s/quiebra). Ccom Capital, en pleno, 27-10-94: “La Razón s/ quiebra”: La tasa activa incluye el spread, diferencia que estaría destinada a la retribución de las labores de intermediación efectuada por las entidades financieras, los gastos administrativos inherentes a la organización empresaria, los costos indirectos derivados de la inmovilización de parte de los depósitos y una justa utilidad” 1 3. Componentes de las tasas activas Las tasas activas se forman teniendo en cuenta diferentes componentes, como ser: Costo de la obtención de los fondos (ej.: tasa pasiva). Aquí influye terminantemente la situación de liquidez de la Entidad. La globalización de los mercados también influye ya que las entidades que tienen acceso al mercado financiero o de capitales externo acceden a un fondeo menos oneroso que aquéllas que no cuentan con esa alternativa. Costos regulatorios (ej.: efectivo mínimo, previsión por morosidad, fondo de garantía de los depósitos) y cargas impositivas. El costo de la morosidad fue contemplado en varios fallos, entre otros: CNCom, sala A, fallo del 8-5-54, CNCom, sala A 16-5-91: “Caperruba c/ Iceta”... . Por ejemplo, la CNCiv., sala J., 13-3-97, dice: “A la calificación del precio que se otorga al interés debe sumarse el carácter de prima por el riesgo asumido por el acreedor de que su deudor caiga en insolvencia y pierda su capital”. Inflación presupuestada –ver desarrollo del punto “4. Moneda”. Un fallo de la CSJN del 33-92: YPF c/ Pcia. de Corrientes dice: “La tasa activa está integrada no solamente por la renta y la depreciación de la moneda, sino también y en gran medida por el …costo generado por la intermediación financiera”. Costos operativos o de administración. La CCCL de Rafaela (Santa Fe) el 27-3-96, en autos Asociación Atlético de Rafaela c/Zurvera y otros” expresa: “.... como ocurre con la actora, por su actividad como depositario del dinero de los ahorristas deba pagarles a éstos un interés, teniendo también que prever el riesgo de incobrabilidad a lo que se deben agregar los gastos de funcionamiento”. Plazo de la operación. El fallo de la C. Comercial, sala D – 1986- indica: “... esa elevación de la tasa de interés tuvo su justificación: fue otorgado un crédito de muy largo plazo, durante el cual es imaginable un elevado costo administrativo que habría de afrontar la mutuante por el hecho de mantener sus oficinas abiertas para liquidar y percibir”. Riesgo (si el préstamo se otorgará con o sin garantía; tipo de empresa, sector, mercado). Otro fallo expresa: “Existen además específicos riesgos sectoriales y particulares inherentes al tomador del crédito, los que crecen o disminuyen atendiendo a las garantías de la operación y al plazo de la misma”. Ganancia. La CA Fed. de Rosario, sala B, Banco Nación c/ Muzzolòn” D y E, Nro. 3 expresa: “El dinero prestado por el Banco tiene un costo comprendido por el interés pasivo más los costos operativos y la ganancia del banco”. En otros fallos también se hace mención a varios de los componentes de las tasas, como ser: La CCCL de Rafaela (Santa Fe) el 27-3-96, en autos Asociación Atlético de Rafaela c/Zurvera y otros” menciona: “..... más aún cuando el acreedor no era un banco, su dinero, la previsión por riesgo de incobrabilidad y el costo de funcionamiento que significa toda la infraestructura y recursos humanos que el banco necesita para cumplir su cometido. El acreedor, como ocurre con la actora, por su actividad como depositario del dinero de los 2 ahorristas debe pagarles a éstos un interés; teniendo también que prever el riesgo de incobrabilidad, a lo que se deben agregar los gastos de funcionamiento. 4. Moneda Al momento de determinar la tasa a aplicar se debe tener en cuenta la moneda en la cual se recibirán o se desembolsarán los fondos. Como ya expresamos en el cálculo de la tasa activa, para las operaciones en moneda nacional, se tendrá en cuenta la tasa de inflación prevista. Diferentes fallos tomaron en cuenta este punto, p. ejemplo: “Las altas tasas de interés comprenden no solamente el precio por el uso del dinero prestado sino el premio por el desgaste del capital nominal, o el reembolso de la pérdida de su valor adquisitivo al tiempo de la devolución (CACiv..Cap. Fed. Salas A, D E y F E D ts. 54, 57 y 58, ps. 525, 200, 499, 510, 469 y 509 respectivamente)”. En cambio, en las operaciones en moneda extranjera la tasa es menor porque este elemento – inflación del país- no contará para su determinación. Pero sí será importante, la incidencia del tipo de cambio al momento de realizar la devolución del préstamo. En la última crisis del sistema financiero –año 2001/2002-, existían numerosos deudores de préstamos en moneda extranjera. La tasa aplicada era menor que la correspondiente a las operaciones crediticias en moneda nacional, dado que no contemplaba la inflación de Argentina (porque esos créditos eran en u$s). La situación existente permitió soluciones “sui generis” para la pesificación de las deudas en moneda extranjera, algunas fueron ajustadas por CER (coeficiente de estabilización monetaria) o por CVS (coeficiente de variación salarial) y otras; se convirtieron directamente en moneda nacional y continuaron con la tasa pactada en u$s, a pesar que se abonaban en pesos. En los casos de los préstamos morosos que llegaron a la Justicia, algunos jueces determinaron que el esfuerzo por la incidencia del tipo de cambio debía compartirse (el 50% a cargo del deudor y el resto a cargo de la Entidad Financiera). 5. Tasas nominales y efectivas Las tasas nominales son tasas de referencia anuales a partir de las cuales y dependiendo de la condición de capitalización se obtienen las tasas efectivas. Son las fijadas contractualmente. El periodo de capitalización determina el momento de liquidación o acumulación de los intereses, independientemente de que se paguen o no. Las tasas efectivas muestran el rendimiento o costo de una operación para un determinado periodo de tiempo. Solo en el caso en que el periodo de capitalización es anual, la tasa nominal y la efectiva anual, son iguales. Veamos un ejemplo para clarificar el concepto de tasa nominal y efectiva en una operación a plazo fijo en pesos basándonos en la pizarra de un Banco: 3 Plazo 30 60 ...... TNA (*) TEM (*) 12 % 0,986% 12,50 % 1,02% .... ... (*) Téngase en cuenta que los cálculos se realizaron sobre la base de año civil y no bisiesto (365 días). Existe otra posibilidad de cálculo, considerar que el año se divide en meses de igual cantidad de días (30). Esta otra forma se denomina año comercial (año=360 días). La operación a plazo Fijo en Argentina se realiza sobre la base de año civil. Si una persona desea realizar una inversión a P. Fijo a 30 días en la Institución que publicita las tasas del ejemplo, le pagarán una TNA (tasa nominal anual) del 12%. Si la operación es de $ 1.000, el interés que le corresponderá recibir a los 30 días, será de $ 9,86 (1000*0,12/365*30). Si quiere conocer cuál fue el rendimiento de su inversión, puede comparar el interés recibido con el capital invertido. En este caso, como la operación es por un mes, el resultado será un rendimiento mensual: 0,986%. Este mismo porcentaje se encuentra reflejado en la columna TEM (tasa efectiva mensual) de la pizarra del Banco. También se logra el mismo resultado, proporcionando la TNA (30) por el plazo de la operación (30 días) para obtener la TEM. Es decir, 0,12*30/365=TEM=0,986%. En este simple ejemplo, quedó demostrado que, partiendo de una tasa de referencia anual del 12% para una operación a 30 días, el rendimiento mensual de esa inversión fue del 0,986% (tasa efectiva mensual - TEM -). Ahora, veamos el caso de otra persona que quiere realizar un depósito a plazo fijo a 60 días. La TNA aplicable para esta operación, según la pizarra del mismo banco, sería: 12,5%. Imaginemos que este inversor coloca el mismo importe que el anterior: $ 1000, el interés que deberá recibir al término de los 60 días será de: 1000*0,125/365*60=$ 20,55 Si este inversor quisiera conocer cuál fue el rendimiento de su inversión, realizaría el mismo cálculo que el inversor anterior: 20,55/1000= 2,055% Este resultado expresa el rendimiento de la inversión de 60 días, no el mensual. Este importe no coincide con la pizarra de la Entidad Financiera ya que en la misma se refleja, de acuerdo a normas, la TEM y no la tasa efectiva bimestral. Para poder calcular la TEM de esta operación se debe realizar el cálculo que se indica en el punto: “equivalencias de tasas” –punto 10-. 6. Tasas vencidas y adelantadas: Las tasas vencidas (o de interés) son las que capitalizan (adicionan interés al capital) al final de un periodo determinado. Es decir, convierten una unidad monetaria presente en un monto (capital más interés) unitario en el futuro. 4 Las tasas adelantadas (o de descuento) actualizan un valor nominal futuro transformándolo en un valor actual (o valor presente). Es decir, convierten hoy al valor nominal (capital a cobrar en un futuro) en valor actual (V. Nominal menos descuento). Estas tasas se pueden subdividir en nominales y efectivas. Es decir que, existen tasas nominales anuales de interés, tasas nominales anuales de descuento, tasas efectivas de interés y tasas efectivas de descuento. Para pasar de una tasa vencida a adelantada, se calcula el valor actual de la tasa vencida. Es decir: Tasa vencida/ (1+tasa vencida)= Tasa adelantada, también se puede expresar de la siguiente forma: 1-(1+tasa vencida) -1= tasa adelantada1 7. Tasas fijas y variables Cuando se contrata, se debe prestar especial atención a los temas financieros. Existen posibilidades de tomar préstamos que pueden tomarse a tasa fija o variable. Por ejemplo, analicemos la oferta al 2/8/2012 de un préstamo hipotecario a 5 años –con pago de cuota mensual-. Se puede ver que la diferencia en tasas es importante y llevaría a decidir automáticamente por el préstamo a tasa variable. Préstamo Hipotecario2 A tasa Fija A tasa variable TNA 22% 17,93% TEA 24,36% 19,48% CFT (IVA incluido) 28,87% 23,65% Pero no solo se debe considerar el importe de la tasa para decidir sino también en qué condiciones variará la tasa. En algunos casos el préstamo podría llegar a tornarse financieramente más caro que si se hubiese elegido uno a tasa fija. Hay casos en que la variabilidad de la tasa está condicionada por ejemplo al: Aumento de la tasa Libor (tasa nominal anual internacional de Londres) Aumento de las tasas pasivas promedio Aumento de las tasas activas promedio, etc... Cumple un papel prioritario la determinación de la periodicidad de revisión de la tasa y el plazo total del préstamo. 1 Partiendo de: 1 - ______ 1 = tasa de descuento y sacando común denominador, se llega a la expresión: tasa vencida (1+tasa vencida) (1+tasa vencida) 2 http://www.bancociudad.com.ar 5 Pero, no se debe limitar al sólo análisis de estas variables sino hay que tener en cuenta el costo financiero total –CFT-, que como se notará en el cuadro anterior, muestra cómo sube el costo (ver punto 14). 8. Valor Actual Neto (VAN)3 Para calcular el VAN, se descuenta el flujo de fondos futuro utilizando una tasa de corte determinada (costo del capital). De esta forma se logra valuar el flujo de fondos al momento cero o momento de la inversión inicial. Al importe logrado, se le resta la inversión inicial y se obtiene el valor del VAN. Generalmente, si el VAN es igual o mayor a cero, la propuesta se considera aceptable. En caso contrario, se rechaza. 9. Tasa Directa y sobre saldo Es aceptable que cualquier tomador de préstamo pague intereses sobre saldo de deuda. A medida que el saldo de deuda decrece los intereses se comportan de la misma manera. Se muestra esta situación en un ejemplo de amortización de préstamos por el sistema alemán y por el francés. Los datos utilizados para ambos ejemplos son los siguientes: Importe del préstamo: $ 10 mil Cantidad de cuotas: 4 Periodicidad de la cuota: mensual Tasa de interés: 1% (efectiva mensual) Préstamo abonado por sistema francés – cuotas totales iguales-: Per 0 1 2 3 4 Total Cuota Interés 2.562,81 100 2.562, 81 75,37 2.562,81 50,50 2.562,81 25,37 10.251,24 251,24 Amortización del capital 2.462,81 2.487,44 2.512,31 2.537,44 10.000 Saldo de deuda 10.000 7.537,19 5.049,75 2.537,44 0 Préstamo abonado por sistema alemán – cuotas de amortización de capital iguales- : Per Cuota 0 1 2.600 2 2.575 3 2.550 4 2.525 Total 10.250 3 Interés Amortización del capital 100 75 50 25 250 2.500 2.500 2.500 2.500 10.000 Ver bibliografía indicada en el programa 6 Saldo de deuda 10.000 7.500 5.000 2.500 0 Ahora bien, existen préstamos de cuotas iguales a tasa directa. Si tomamos en cuenta los mismos datos de nuestro anterior ejemplo, el resultado de tomar un préstamo de estas características sería el siguiente: Monto a abonar total: 10000 (1+0,01)4=10.406,04 En cambio si se realizara por capitalización simple con tasa TNA(120) =0,12: Monto a abonar total: 10000 (1+0,12*4/12) =10.400 La cuota se determina dividiendo por la cantidad de periodos el monto recién calculado. Es decir: Cuota= 10406,04/4=2601,51 o Cuota= 10400/4=2600 Obsérvese que el costo de utilizar un sistema de tasa directa es más caro que utilizar el pago sobre saldo de deuda. Total a abonar por sistema francés: $ 10.251,24 Total a abonar por sistema alemán: $ 10.250 Total a abonar por aplicación de tasa directa: $ 10.406,04 o 10.400. 10. Equivalencia de tasas: Dos tasas efectivas son equivalentes cuando a un mismo capital en una misma cantidad de tiempo le hacen corresponder el mismo monto. Se puede decir también que dos tasas son equivalentes cuando producen el mismo monto unitario (para un capital de $1) en el mismo periodo de tiempo. Volvamos al caso de la inversión en plazo fijo: Recordemos: el inversor que hizo una operación a 30 días, obtuvo una tasa efectiva mensual (TEM) de 0,986%. En cambio el que hizo una operación de 60 días, su rendimiento efectivo a 60 días fue de 2,055% Para poder comparar estos rendimientos, habría que llevar la TEM de la primera operación a una tasa efectiva de 60 días o la tasa efectiva de 60 días correspondiente a la segunda operación a una tasa efectiva mensual. Antes de resolverlo, recordemos la definición que dimos de tasas equivalentes: “son aquellas que producen mismo monto unitario”. Un monto es la adición al capital del interés. Si se habla de monto unitario es aquél producido por un capital de $1. Entonces, en nuestro ejemplo, debemos comparar los montos unitarios a 30 y 60 días y hacerlos equivalentes: (1+ TEM) = (1+ TE(60)). 7 Lo que se muestra no es una igualdad porque cada uno de los términos está expresado para periodos diferentes. Uno es un monto para 30 días y el otro, lo es para 60. Se puede transformar el monto de 30 en uno de 60 días, elevando al cuadrado el primer término (porque 60 días son 2 meses). La ecuación quedaría de esta forma: (1+TEM) 2 = (1+ TE(60)) Ahora si los dos términos están expresados para el mismo periodo de tiempo (60 días). El dato que se conoce es la TEM del primer inversor: 0,986%, entonces: (1+0,00986) 2 = (1+TE(60)) Resolviendo la cuenta y restando el 1, tendríamos la TE(60) equivalente a la TEM del primer inversor. 1,01981722 -1=TE(60)= 0,01981722=1,98% Si recordamos la TE(60) correspondiente a la operación del segundo inversor fue 2,055% y la comparamos con la que obtuvimos en el cálculo anterior (1,98%), nos damos cuenta que el segundo inversor tuvo mejor rendimiento. Esto surgía de ver la pizarra del Banco, la cual mostraba que la TEM para un plazo fijo a 30 días era de: 0,986% y la TEM para la operación de 60 días era de: 1,02%. El Banco para calcular la TEM de la operación de 60 días, realizó el siguiente cálculo: (1+0,02055)1/2 –1= TEM=0,0102 =1,02% 4 Si se tuviera que calcular la tasa adelantada efectiva mensual partiendo de la tasa efectiva para 60 días del 2,055%; debemos volver sobre el concepto estudiado al final del punto 6. El monto unitario se debe transformar en un valor actual: Monto unitario= (1+tasa vencida). En el ejemplo (1+0,02055)= monto unitario para 60 días Valor actual= (1+tasa vencida) -1. En el ejemplo, el valor actual para 60 días sería: (1+0,02055) -1 Pero lo que se busca es la tasa adelantada para 60 días, entonces, siguiendo el razonamiento realizado en el punto 6., debemos restarle a 1 este valor actual logrado. Entonces, el cálculo sería: 1-(1+0,02055) -1= tasa de descuento o adelantada efectiva para 60 días= TEad(60) 11. Tasa real y tasa aparente Las tasas contienen un componente inflacionario, cuando se refieren a operaciones en monedas de un País con inflación. Cuando se fijan las tasas, tanto sea para operaciones de inversión como crediticias, la inflación del periodo futuro no se conoce de antemano, por ello se presupuesta la misma. Las tasas en periodos inflacionarios se denominan aparentes. 4 se puede elevar a ½ porque se necesita un mes de los dos de la tasa 8 Imaginemos la siguiente operación crediticia: Capital prestado: $ 1.000 Inflación estimada para próximos 60 días: 10% Tasa que contiene: prima de riesgo y ganancia: 3% (por los 60 días) ¿Cuál es la tasa que se le impondrá al deudor para que abone su operación crediticia (por los 60 días)? (1,10*1,03)-1= 0,133. Esta tasa efectiva para 60 días es aparente. La otra forma de calcular esta tasa es: I/C o (C(n) –C) C donde: I = es Interés C= es Capital I = C * TNA * n/ut (TNA * n/ut =tasa efectiva de la operación) C(n)= Monto= C+I I= (1.000*1,10*1,03) – 1.000=133 C(n)= 1.000 +133= 1.133 Tasa efectiva aparente para 60 días (tiempo de la operación) = 133/1000 o (1.1331000)/1000=0,133. Ahora bien, esta tasa aparente en periodos inflacionarios no nos está indicando si mantuvimos o no el poder adquisitivo, lo cual es medido por medio de la tasa real (aquella que expresa el poder adquisitivo de la tasa de interés). Para calcular esta tasa real, se parte de la tasa aparente y se separa de la misma el componente inflacionario - inflación realmente sucedida- del siguiente modo: Tasa real= 1 + tasa aparente - 1 1+tasa de inflación Entonces, partiendo de la tasa aparente del 13,30% calculemos las tasas reales para el prestamista (acreedor), suponiendo 3 posibilidades de inflación realmente sucedida: a) Inflación: 13,30%. Cálculo de tasa real= ((1+0,133)/(1+0, 133)) – 1= 0% (tasa real neutra) b) Inflación: 7%. Cálculo de tasa real= ((1+0,133)/(1+0, 07)) – 1= 0,0588 (tasa real positiva) c) Inflación: 16%. Cálculo de tasa real= ((1+0,133)/(1+0, 16)) – 1= -2,33%(tasa real negativa) ¿Qué significa tasa real positiva, neutra o negativa? Cómo ya expresamos la tasa real refleja la pérdida o no del poder adquisitivo. Con una tasa real negativa se registra pérdida de poder adquisitivo. Mientras que una tasa real positiva permitirá la adquisición de mayor cantidad de bienes y una tasa real neutra, implicará que se mantuvo el poder adquisitivo. 9 En Argentina existen diferentes índices o coeficientes para ajustar las operaciones, algunos de ellos son: 1) IPC: Indice de Precios al Consumidor calculado por Indec. 2) CVS: índice de salarios calculado por Indec. Mide las variaciones de los salarios tanto del sector público como del sector privado en cada mes (se obtiene con datos de encuesta) 3) Indice de Precios Mayoristas (IPM) nivel general, calculado por el Indec. 4) CER: Coeficiente de estabilización de referencia. Creado a partir de 2002 y es difundido por BCRA. Para su cálculo diario se toma el índice de precios al Consumidor (IPC) 12. Tasa Interna de Retorno (TIR)5 La tasa interna de retorno es la tasa que se utiliza para descontar el flujo de fondos y permite igualar el valor actual de esos flujos de fondos futuros con el valor de la inversión inicial. 13. Publicidad de las tasas de Interés El Banco Central reglamenta cómo se deben exponer las tasas de interés para defender los intereses de los que contratan con la Entidad Financiera y para lograr una mayor transparencia en el mercado. Además de lo que reglamenta BCRA, el primero de los deberes que exige la buena fe es la debida, concreta y veraz información. La Ley de Defensa del Consumidor vigente consagra la protección de los intereses económicos de los consumidores y usuarios, otorgándoles derecho a una información adecuada y condiciones de trato equitativo y justo. Este derecho tiene explícita base constitucional (art. 42 C.N.). Fundamentan estas exigencias el reconocimiento de la desigualdad de las partes contratantes. El BCRA dispone diferentes medidas a tener en cuenta por las Entidades Financieras: a) En los recintos de las Entidades Financieras En las pizarras de los locales de atención al público se deben colocar información sobre las tasas de interés de las líneas de crédito (hipotecario, prendario, comercial, tarjetas de crédito) ofrecidas a los clientes, por operaciones en pesos, en moneda extranjera o en títulos valores, con el siguiente detalle: 5 Tasa de interés nominal anual. Tasa de interés efectiva anual. Costo financiero total en los créditos de operatorias específicas (tales como préstamos hipotecarios para vivienda o prendarios para automotores). La mayor y la menor de las tasas de interés, cuando respecto de la línea expuesta exista más de una tasa. Ver bibliografía indicada en el programa 10 Tasa de interés activa promedio ponderada por operaciones concertadas en el mes anterior al que corresponda. En todos los casos, las tasas deberán expresarse en tanto por ciento con dos decimales. b) En otros medios o lugares. Al publicitar en medios gráficos (periódicos, revistas, carteleras en la vía pública o en obras en construcción, etc.) créditos hipotecarios para vivienda, prendarios para automotores, al mencionar la cantidad de cuotas y/o el importe de ellas y/o la tasa de interés, debe exponerse en forma legible y destacada lo siguiente: Tasa de interés nominal anual. Tasa de interés efectiva anual. Costo financiero total. Carácter fijo o variable de la tasa de interés. Las tasas deberán exponerse en tanto por ciento con dos decimales, discriminando las que correspondan a operaciones en pesos de las de moneda extranjera. En cambio, si la publicidad se realiza en forma radial o televisiva, cuando se haga referencia a importes de cuotas o tasas, se deberá informar exclusivamente el costo financiero total. Publicidad de cuotas: cuando se publicitan valores de cuotas de préstamos hipotecarios o prendarios, deben incluirse todos los conceptos que estarán a cargo de los prestatarios (amortización de capital, interés, primas por seguros exigidos en el contrato, gastos de mantenimiento de cuentas asociadas al préstamo, impuestos, etc.) 14. Expresión de las tasas. Las tasas de interés deberán expresarse en forma homogénea y transparente dentro del mercado financiero con la finalidad de que los usuarios del crédito dispongan de elementos comparables para su evaluación. 1) Exposición en los documentos. En todas las operaciones, cualquiera sea su instrumentación, corresponde que en los contratos, recibos, notas de debito u otros documentos de relación con los clientes, donde se expliciten tasas o importes de intereses, se deje expresa constancia de los siguientes aspectos: i) Tasa de interés o de descuento anual contractualmente pactada, en tanto por ciento con dos decimales. ii) Tasa de interés efectiva anual equivalente al cálculo de los intereses en forma vencida, en tanto por ciento can dos decimales. iii) Carácter fijo o variable de la tasa de interés, con indicación en este último caso de los parámetros que se emplearán para su determinación y periodicidad del cambio. 11 iv) Costo financiero total –CFT-: expresado en forma de tasa efectiva anual, en tanto por ciento con dos decimales. Se determina agregando a la tasa de interés el efecto de los cargos asociados a la operación, cualquiera sea su concepto, en la medida que no impliquen la retribución de un servicio efectivamente prestado o un genuino reintegro de gastos. En operaciones pactadas a tasa variable, para el cálculo del costo financiero total se tomará en cuenta la tasa vigente al momento de su concertación, indicando expresamente que ese costo se modificará en función de la variación que experimente la tasa de interés. Por ej., en los casos de préstamos hipotecarios, para calcular y exponer el CFT, se debe incluir el seguro de vida y desempleo, el seguro de incendio, los gastos de administración, los gastos de evaluación y/o tasación y los gastos de otorgamiento. Todos los conceptos enunciados deberán incluir el Impuesto al Valor Agregado (I.V.A) 12 Cuadro resumen de los diferentes regímenes Régimen Interés/Descuento periódico Tasa Capitalización/ Actualización Fórmulas de MontoInterés V(0)-Descuento Interés Simple Constante TNA C(n)=C(1+TNA/ut*n) I=C*TNA/ut*n Descuento Racional Decreciente TNA Descuento Comercial, Simple o bancario Contante TNA ad m=n (una cap. coincidente con el plazo) m=n (una act coincidente con el plazo) m=n (una act. coincidente con el plazo) Interés Compuesto Creciente TE (m≠n) Cap. Periódica Descuento Compuesto Decreciente TEad (m≠n) Act. Periódica Capitalización Continua Creciente δ (m≠n) Cap. continua 13 V(0)=N(1+TNA/ut*n)-1 D=N(1-(1+TNA/ut*n)-1) V(0)=N(1-TNAad/ut*n) D=N*TNAad/ut*n C(n)=C(1-TNAad/ut*n)-1 I=C((1-TNAad/ut*n)-1-1) C(n)=C(1+TE)n I=C((1+TE)n-1) V(0)=N(1+TE)-n D=N(1-(1+TE)-n) V(0)= N(1-TEad)n D=N(1-(1-TEad)n) C(n)=C(1-TEad)-n I=C((1-TEad) –n -1) C(n)=C*e δ I=C(eδ-1) V(0)= N*e- δ D=N (1- e- δ) RENTAS Surgen de la asociación de una serie de intervalos de tiempo con una sucesión de pagos o de cobros. Por ejemplo los alquileres, cuotas de préstamos, cuotas de colegios, depósitos que se realizan en fondos de pensión y jubilación, bonos, cuotas de un contrato de leasing, etc. En resumen, en donde existe una corriente de pagos o cobros, puede estar involucrada una renta. En las rentas se pueden presentar tres prestaciones básicas: Prestaciones que se resuelven con una serie de contraprestaciones (préstamos y rentas propiamente dichas). Serie de prestaciones que se resuelven con una contraprestación (depósitos que constituyen un fondo, imposición). Serie de prestaciones que se resuelven con otra serie de contra prestaciones (jubilación). CLASIFICACIÓN DE RENTAS 1. Por tiempo de duración: a) Temporarias: se conoce de antemano los momentos en los que ha de comenzar y terminar la serie de pagos. Ej. Préstamos, bonos. b) Perpetuas: se conoce el momento de empezar a funcionar pero no cuándo termina la serie. Ej.: Bonos de Estados Unidos a 30 años en los que nunca amortiza el capital. 2) En función de la medida de los períodos que componen las rentas: a) Períodos iguales: cuando los aportes, rentas, etc. son fracciones de tiempos iguales; b) Períodos distintos. 3) Por la forma de capitalizar o descontar intereses: a) Interés simple b) Interés compuesto. 4) En función de la amplitud de los períodos: a) Discretas o discontinuas: todos los períodos son finitos. Pueden ser medibles (ej. 1 mes, 1 año); 14 b) Continuas: los períodos son infinitamente pequeños. No son medibles. 5) Por la relación entre la frecuencia de pago y la de capitalización: a) Sincrónicas: cuando coinciden ambas frecuencias; b) Asincrónicas: cuando no coinciden ambas frecuencias (ej. pago mensual con capitalización trimestral.) 6) En función del importe de cada pago o término: a) Cuotas constantes: todas las cuotas son iguales; b) Cuotas variables: las cuotas no son iguales. 7) Por el momento en que se realizan los pagos: a) Vencidas: cuando los pagos se efectúan al final de cada uno de los períodos que conforman el tiempo de la renta; b) Adelantadas: cuando los pagos se realizan al principio de cada período 8) En función del comportamiento de la tasa: a) Tasa fija: la tasa efectiva periódica de interés es la misma en todos los períodos; b) Tasa variable: la tasa efectiva periódica de interés no es igual en todos los períodos. 9) En función del comienzo y finalización del período de pago: a) Ciertas: se conoce de antemano cuando comienza o termina el pago y el importe de cada uno de los pagos; b) Aleatorias: cuando se incluye en la renta la condición que para comenzar o finalizar la corriente de pagos debe ocurrir un hecho azaroso, ajeno a la voluntad de las partes. 10) Por el período en el que se inicia la sucesión de pagos y aquel en el cual se valúan las cuotas: a) Inmediatas: los pagos se inician en el período en el cual se valúan las cuotas; b) Diferidas: el comienzo de los pagos está desplazado hacia la derecha respecto del momento de la valuación de las cuotas. Al tiempo comprendido entre el momento de valuación y el de comenzar los pagos se llama período de gracia o diferimiento; c) Anticipadas: el comienzo del pago de las cuotas es anterior al de la valuación. Está formada por una imposición y luego por una renta inmediata. 15 11) Por su finalidad: a) Rentas de capitalización: aquellas con las cuales se busca llegar a un capital disponible en el futuro mediante una inversión periódica de recursos monetarios. Ej.: círculo de ahorro previo. b) Rentas de amortización: con el uso de estas rentas se busca cancelar una deuda mediante una serie de pagos periódicos (préstamos) o el agotamiento de un fondo (renta propiamente dicha). c) Rentas mixtas: son una combinación de las anteriores. Ej.: jubilación privada. 16