MOVIMIENTOS EN EL PLANO
Anuncio
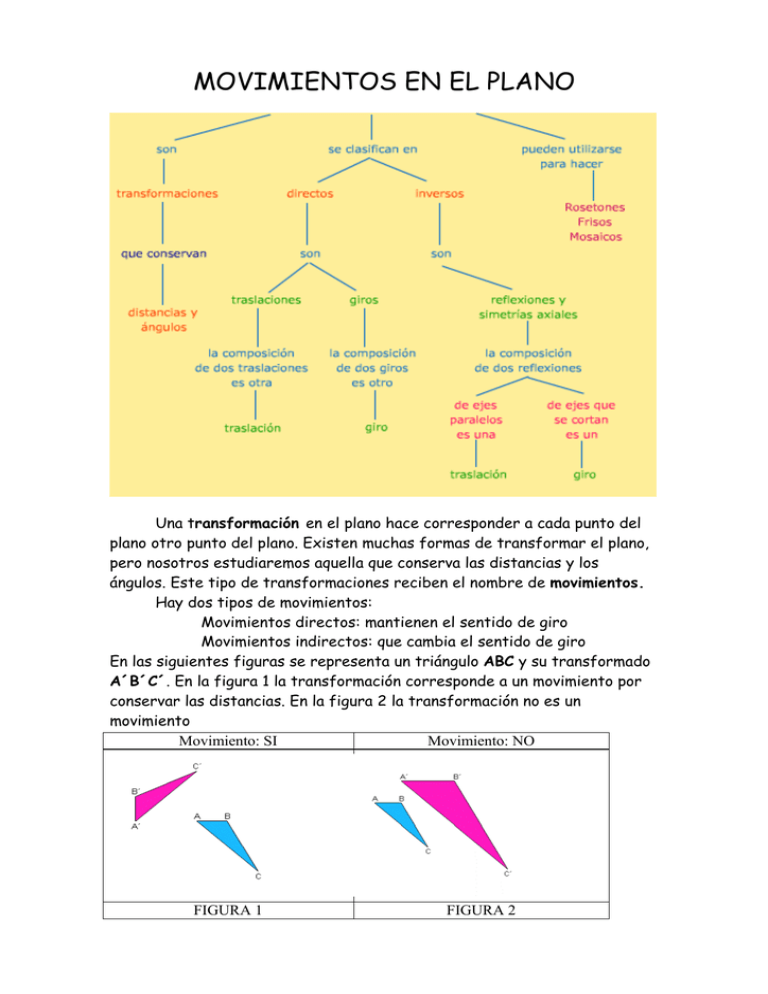
MOVIMIENTOS EN EL PLANO Una transformación en el plano hace corresponder a cada punto del plano otro punto del plano. Existen muchas formas de transformar el plano, pero nosotros estudiaremos aquella que conserva las distancias y los ángulos. Este tipo de transformaciones reciben el nombre de movimientos. Hay dos tipos de movimientos: Movimientos directos: mantienen el sentido de giro Movimientos indirectos: que cambia el sentido de giro En las siguientes figuras se representa un triángulo ABC y su transformado A´B´C´. En la figura 1 la transformación corresponde a un movimiento por conservar las distancias. En la figura 2 la transformación no es un movimiento Movimiento: SI Movimiento: NO FIGURA 1 FIGURA 2 En una transformación, un punto se llama doble cuando su transformado es él mismo. Una recta es doble si su transformada es ella misma. Ejercicio 1.-Indica si las siguientes afirmaciones son ciertas a) Una transformación es un movimiento. b) Un movimiento conserva siempre la forma. c) Una transformación mantiene el tamaño de las figuras. Vectores Dos puntos del plano A y B, determinan un vector fijo AB , en el que A es el origen y el B el extremo. La distancia entre A y B (longitud del segmento AB) se llama módulo del vector y la recta que pasa por A y B es la dirección del vector. El sentido es el que va de A a B. Dados dos puntos A (a1, a2) y B (b1, b2), las coordenadas del vector AB , son (b1- a1 , b2 - a2). Así por ejemplo: Las coordenadas de los puntos A y B de la figuras son: A (2, 3) y B (5, 5) Por tanto las coordenadas del vector AB son: AB = (5-2, 5-3) = (3, 2) TRASLACIÓN: Se denomina traslación definida por un vector dado v al movimiento que hace corresponder a cada punto A del plano otro punto A’ tal que el vector definido por A y A’ tiene los mismos módulo, dirección y sentido que el vector dad v. Propiedades: Son movimientos directos No hay puntos dobles Cualquier recta paralela al vector traslación es doble. GIRO: Se denomina giro de centro un punto O del plano y ángulo orientado ϕ, al movimiento que transforma un punto A en otro A’ tal que OA = OA’ y el ángulo AOA’, con vértice en O es igual en amplitud y sentido al ángulo ϕ. Propiedades: Son movimientos directos El centro de giro O es un punto doble Las circunferencias de centro O son figuras dobles. SIMETRÍA AXIAL: Se denomina simetría axial de eje una recta dada e a una transformación que hace corresponder a cada punto A del plano otro punto A’ de forma que la recta e sea mediatriz del segmento AA’. Propiedades: Son movimientos inversos Todos los puntos de e son dobles Las rectas perpendiculares a e son dobles Paginas web recomnendadas: Página donde está todo muy concreto, hay información sobre frisos etc.: http://www.telefonica.net/web2/m-p/index.htm Página donde se representa todos los movimientos, se puede resolver problemas propuestos: http://www.isftic.mepsyd.es/w3/eos/MaterialesEducativos/mem2003/movimientos/ Página donde aparecen figuras al que se les aplica movimientos: http://recursos.pnte.cfnavarra.es/~msadaall/geogebra/movimientos.htm Página donde se explica los movimientos, con ejemplos con aplicaciones, también tienen la composición de movimientos. http://concurso.cnice.mec.es/cnice2006/material105/inicio.html Pagina donde se explica los movimientos, desde un punto de vista de dibujo. http://www.educacionplastica.net/movimien.htm







