Soluciones

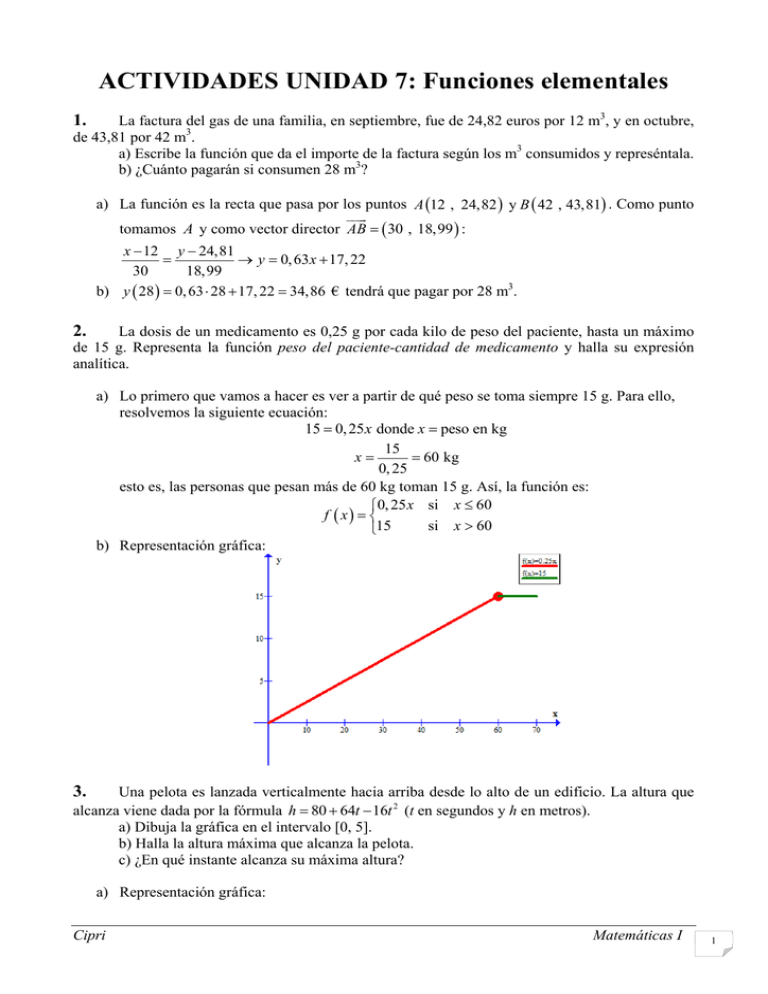
ACTIVIDADES UNIDAD 7: Funciones elementales
La factura del gas de una familia, en septiembre, fue de 24,82 euros por 12 m3, y en octubre,
de 43,81 por 42 m3.
a) Escribe la función que da el importe de la factura según los m3 consumidos y represéntala.
b) ¿Cuánto pagarán si consumen 28 m3?
1.
a) La función es la recta que pasa por los puntos A 12 , 24,82  y B  42 , 43,81 . Como punto

tomamos A y como vector director AB   30 , 18,99  :
x  12 y  24,81

 y  0, 63 x  17, 22
30
18,99
b) y  28   0, 63  28  17, 22  34,86 € tendrá que pagar por 28 m3.
2.
La dosis de un medicamento es 0,25 g por cada kilo de peso del paciente, hasta un máximo
de 15 g. Representa la función peso del paciente-cantidad de medicamento y halla su expresión
analítica.
a) Lo primero que vamos a hacer es ver a partir de qué peso se toma siempre 15 g. Para ello,
resolvemos la siguiente ecuación:
15  0, 25 x donde x  peso en kg
15
x
 60 kg
0, 25
esto es, las personas que pesan más de 60 kg toman 15 g. Así, la función es:
0, 25 x si x  60
f  x  
si x  60
15
b) Representación gráfica:
3.
Una pelota es lanzada verticalmente hacia arriba desde lo alto de un edificio. La altura que
alcanza viene dada por la fórmula h  80  64t  16t 2 (t en segundos y h en metros).
a) Dibuja la gráfica en el intervalo [0, 5].
b) Halla la altura máxima que alcanza la pelota.
c) ¿En qué instante alcanza su máxima altura?
a) Representación gráfica:
Cipri
Matemáticas I
1
Para representar la parábola anterior, calculamos el vértice y los puntos de corte con los
ejes:
Vértice:
b
64
tv 

2
2a 2   16 
hv  h  2   80  64  2  16  22  144
Puntos de corte con el eje OX:
1
80  64t  16t 2  0  t  
5
Punto de corte con el eje OY:
t  0  h  80
b) La altura máxima que alcanza la pelota es de 144 m.
c) Dicha altura la alcanza a los 2 segundos de haberla lanzado.
4.
Un fabricante vende mensualmente 100 electrodomésticos a 400 euros cada uno y sabe que
por cada 10 euros de subida venderá 2 electrodomésticos menos.
a) ¿Cuáles serán los ingresos si sube los precios 50 euros?
b) Escribe la función que relaciona la subida de precio con los ingresos mensuales.
c) ¿Cuál debe ser la subida para que los ingresos sean máximos?
a) A 450 € vende 90 electrodomésticos, luego sus ingresos en este caso serán de:
450  90  40 500 €
I  x   ingresos en función del número de decenas de € subidos =
b)
= precio  nº de electrodomésticos   400  10 x 100  2 x   20 x 2  200 x  40 000
c) El máximo se obtiene en el vértice de la parábola I  x  :
b
200

5
2a 2   20 
La subida debe ser de 5 decenas de euros, es decir, 50 € para que los ingresos sean máximos.
xv 
5.
Un vendimiador ha de recoger 10 000 kg de uva que hoy vendería a 50 céntimos el kilo.
Cada día que pasa se estropean 500 kg y el precio aumenta en 5 céntimos el kg. ¿Cuánto ha de
vendimiar para obtener el máximo beneficio y cuál será éste?
a) La función beneficio es:
B  t   10000  500t  50  5t   500 000  25 000t  2 500t 2
Departamento de Matemáticas
2
b) El beneficio máximo lo obtiene en el vértice de la parábola:
25 000
tv 
 5 días
2   2500 
y dicho beneficio máximo es de B  5   562 500 cent = 5 625 €
6.
Los controles de calidad de una cadena de montaje de ordenadores han obtenido que el
porcentaje de ordenadores que siguen funcionando al cabo de t años viene dado por:
t
4
p  t   100  
5
a) Representa gráficamente esta función.
b) ¿Tiene sentido real toda la gráfica obtenida?
c) ¿Qué porcentaje de ordenadores siguen funcionando al cabo de dos años? ¿Y al cabo de
cinco años?
d) ¿Qué significado tiene el punto de corte con el eje de ordenadas?
e) ¿Cuánto tiempo ha de pasar para que el porcentaje de ordenadores que sigan funcionando
sea del 80 %? ¿Y para que funcionen la mitad?
a) Representación gráfica (se hace construyendo una tabla de valores positivos)
b) No, solo para los valores positivos de la variable independiente, que en este caso es el
tiempo  t  .
2
c)
4
p  2   100     64
5
Es decir, el 64 % de los ordenadores siguen funcionando al cabo de 2 años.
5
4
p  5   100     32, 77 %
5
Es decir, el 64 % de los ordenadores siguen funcionando al cabo de 2 años.
d) El número de ordenadores que se han analizado para llevar a cabo dicho control de calidad,
que en este caso es el 100 %.
e) Para que sigan funcionando el 80 %:
t
t
t
80  4 
4 4
4
p  t   80  80  100    
        t 1
100  5 
5 5
5
Al cabo de 1 año siguen funcionando el 80 % de los ordenadores.
Cipri
Matemáticas I
3
Para que sigan funcionando la mitad: 50 %
t
t
t
t
50  4 
1 4
1
4
4
p  t   50  50  100    
        log  log   
100  5 
2 5
2
5
5
1
log
1
4
2  3,1
 log  t  log    t 
2
4
5
log  
5
Al cabo de 3,1 años (que son 3 años, 1 mes y 6 días1) siguen funcionando el 50 % de los
ordenadores.
7.
Algunas flores como los tulipanes se reproducen por medio de bulbos. Supongamos que un
bulbo de tulipán origina otros 5 nuevos que se plantan al año siguiente. Calcula el número de
tulipanes que habrá al cabo de 5 años. ¿Cuántos años han de pasar para que haya 15 625 tulipanes?
Encuentra la fórmula que describe la multiplicación de los tulipanes.
a) La función que da el número de gladiolos al cabo de t años es: N  t   5t
b) Al cabo de 5 años habrá N  5   55  3 125 gladiolos
c) Para que haya 15 625 gladiolos han de pasar:
15 625  5t  56  5t  t  6 años
8.
Un cultivo de bacterias comienza con 100 células. Media hora después hay 435. Si ese
cultivo sigue un crecimiento exponencial del tipo y  ka t (t en minutos), calcula k y a y representa
la función. ¿Cuánto tardará en llegar a 5 000 bacterias?
a) N  t   k  a t donde t = minutos y N  t   número de células
N  0   100  100  k  a 0  k  100
N  t   100  a t
1
b) t  h  30 min.
2
N  30   435  100  a 30  435  a 30 
N  t   100 1, 05t
435
1
 4,35  a  30 4,35  4,35 30  1, 05
100
c) Representación gráfica:
1
Tomando como referencia meses de 30 días.
Departamento de Matemáticas
4
d) N  t   5000  5000  100 1, 05t  t 
log10 50
 80,18 min  1 h 20 min 11 seg
log10 1, 05
9.
En la perforación de un pozo el coste de la extracción del metro cuadrado de tierra a una
profundidad de x metros es proporcional a x a , para un cierto número a  1 . Llamaremos C  x  al
coste de la extracción de tierra del pozo, desde la superficie hasta una profundidad de x metros.
Sabiendo que C  2   8 2C 1 , se pide:
a) Calcular a .
b) Hallar la profundidad h para que C  h   128C 1 .
a) La función es de la forma C  x   k  x a
b) Calculamos a :
C 1  k
C  2   8 2  C 1  8 2k  k  2a  8 2k  2a  23  2 2  2 2  a 
1
c) Sustituimos en la expresión
10.
C  x  k  x
7
7
7
2
2
C  h   128  C 1  k  h 2  128  k  h 2  27  h  4 m
7
7
De todos los pares de números que suman 18, ¿cuál es el par cuyo producto es máximo?
Sean x e y los números buscados. Tenemos que resolver el siguiente problema:
 x  y  18

 xy  máximo
Como x  y  18  y  18  x sustituimos en el producto, que representaremos por p :
p  xy  x 18  x   18 x  x 2 . Por tanto, lo que tenemos que hacer es maximizar la función
p  x   18 x  x 2 , que sabemos que tiene su máximo en el vértice de la parábola:
b
18

9
2a 2   1
Así, uno de los números es 9 y el otro es 18 – 9 = 9, y el producto máximo es 81.
xv 
11.
Tras la aparición de una cierta enfermedad infecciosa, el número de afectados viene dado
por la función p(t )  48t 2  2t 4 , siendo t el número de días desde que se detectó el primer caso. Se
pide:
a) ¿Cuántos días transcurrirán hasta que la enfermedad deje de propagarse?
b) ¿Cuándo aumenta el número de personas afectadas? ¿Cuándo disminuye?
c) ¿Cuándo se detecta el número máximo de personas afectadas? ¿Cuántas son las personas
afectadas en ese momento?
Teniendo en cuenta la representación gráfica:
a) Han de transcurrir 3,5 días para que la enfermedad deje de propagarse.
b) El número de personas afectadas aumenta hasta el tercer día y medio y desde ahí hasta el 4,9
día disminuye.
c) El número máximo de personas afectadas se detecta el día 3,5 y en ese momento hay 290
personas afectadas.
Cipri
Matemáticas I
5
Supongamos que el momento actual corresponde al valor x  0 de la variable tiempo y que
las pérdidas o ganancias  y  de una empresa que acaba de fundarse siguen una función del tipo
12.
y   x  1  1 . Basándose en la representación gráfica de esa función determinar:
a) Los intervalos de tiempo en que la empresa tiene pérdidas y en cuáles tiene ganancias.
b) En qué momento tiene la mayor pérdida.
c) En qué momento no tiene ni pérdidas ni ganancias.
2
Es decir, la empresa tiene pérdidas desde la hora de apertura
hasta transcurridas dos horas. A partir de ahí tiene
ganancias.
La mayor pérdida la tiene precisamente cuando transcurre
una hora desde la apertura, siendo esta pérdida – 1.
No tiene pérdidas ni ganancias cuando y  0 , es decir,
0
cuando x   , esto es, a la hora de apertura y las dos horas
2
de haber abierto.
13. En un estudio sobre el coste de producción de una empresa de ordenadores, se ha concluido
que producir x unidades de un determinado componente tiene un coste expresado por la función
f  x   0, 01x 2  x  1 . La venta de x unidades de ese componente proporciona unos ingresos que
vienen determinados por la función g  x    6  0, 25 x  x , siendo x el número de unidades
producidas.
a) Calcular el número de unidades que deben producir para que los costes sean mínimos.
b) Hallar la expresión, en función de x , de los beneficios, suponiendo que se venden todas
las unidades que se producen.
c) Calcular el número de unidades que deben producir y vender para que los beneficios sean
máximos.
a) Hay que minimizar el coste:
f  x   0, 01x 2  x  1
x
1
 50
0, 02
Departamento de Matemáticas
6
Habría que producir – 50 unidades (el problema está mal planteado).
b) Beneficio:
B  x   g  x   f  x    6  0.25 x  x   0.01x 2  x  1 
6 x 2  125 x  25
25
c) Nos piden maximizar B  x  :
Vértice: x  
125
12
Es decir, la función no tiene máximo (cosa
que se puede apreciar en la gráfica).
La temperatura T  de una reacción química en un laboratorio de productos agrícolas viene
14.
dad, en función del tiempo t en horas, por la expresión T t   2t  t 2 para 0  t  2 .
a) ¿Qué temperatura habrá a los quince minutos?
b) ¿En qué momento volverá a alcanzarse esta misma temperatura?
c) Halla las temperaturas máxima y mínima alcanzadas y lo momentos en que se producen.
15 minutos equivalen a 0,25 horas
a) T (0, 25)  2  0, 25  0, 252  0,50  0, 0625  0, 4375
b) 2t  t 2  0'4375 es de 2º grado, cuyas soluciones son:
x1 = 0,25 y x2 = 1,75; la x1 ya la sabíamos. Por tanto se
repite al cabo de 1 hora y ¾ de hora.
c) Hallamos los máximos y mínimos de la función T(t) y
hallamos un máximo en t = 1 y no tiene mínimos pero observando la gráfica y el problema, tenemos
mínimos en t = 0 y t = 2 horas.
La temperatura máxima se alcanza cuando t = 1 hora con un valor de T (1)  2 1  12  1 ºC
La temperatura mínima se alcanza cuando t = 0 y cuando t = 2 horas con un valor de CERO grados.
1
Dada la función f  x    x 2  3 .
3
a) Representa gráficamente f .
b) Estudia su continuidad en x  3 .
15.
a) Representación gráfica:
Cipri
Matemáticas I
7
b) Continuidad en x  3 .
Gráficamente se ve que la función es continua en x  3 . Vamos a verlo analíticamente:
 x  3  y  0
. Esto se escribe  lim f  x   0

x 3
 x  3  y  0
Por otro lado como f  3  0 y lim f  x   0  f  3  f  x  es continua en x  3
x 3
(Esto no entra en el examen, es simplemente una forma de introducirnos en el tema
siguiente).
Departamento de Matemáticas
8