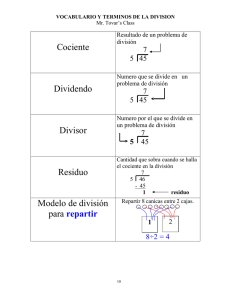
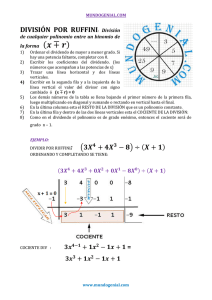
Operaciones Aritméticas en Números con Signo
Anuncio

Operaciones Aritméticas en Números con Signo M. en C. Erika Vilches Parte 3 Multiplicación sin Signo Reglas básicas para multiplicar bits: 0x0 = 0 0x1 = 0 1x0 = 0 1x1 = 1 Ejemplos en números sin signo: Ejercicio: Multiplicar 1101 x 1010 (sin signo) Multiplicación con Signo • El signo del producto depende de los signos del multiplicando y el multiplicador: • Signos iguales → Producto positivo • Signos diferentes → Producto negativo ++=+ +-=-+=--=+ • Cuando se multiplican dos números, ambos deben estar en binario real (sin complementar). Procedimiento para la multiplicación binaria con signo: 1. Determinar los signos del multiplicando (primer operando) y el multiplicador (segundo operando) son iguales o diferentes. Esto determinara el signo del producto. 2. Cambiar cualquier número negativo a su forma real (sin complementar) 3. Empezando con el bit menos significativo del multiplicador, generar los productos parciales. Recorrer un bit a la izquierda cada producto parcial sucesivo. 4. Sumar cada producto parcial sucesivo a la suma de los productos parciales previos para obtener el resultado. 5. Si el bit de signo determinado en el paso 1 es negativo, aplicar complemento a dos al producto. Si es positivo, dejar en forma real. Añadir el bit de signo al resultado. Ejemplo: Multiplicar el número con signo: 01010011 (multiplicando) y 11000101 (multiplicador) 1. El bit de signo del multiplicando es 0 y el bit de signo del multiplicador es 1. El bit de signo del producto será 1 (negativo). 2. Obtener el complemento a dos del multiplicador para ponerlo en forma real. 11000101 → 00111011 3. (y 4.) Proceder con la multiplicación de la siguiente forma 5. Dado que el signo del producto es 1 (como se determino en el paso 1), obtener el complemento a 2 del producto 1001100100001 → 0110011011111 6. Añadir el bit de signo: 1 0110011011111 División sin Signo • La división en binario utiliza el mismo procedimiento que la división en decimal Ejemplos en números sin signo: Ejercicio: Dividir 1100 entre 10 (sin signo) División con Signo • El signo del cociente depende de los signos del dividendo y del divisor: • Signos son iguales → cociente es positivo • Signos son diferentes → cociente es negativo ++=+ +-=-+=--=+ • Cuando se dividen dos números, ambos deben estar en binario real (sin complementar). Procedimiento para la división binaria con signo: 1. Determinar los signos del dividendo (primer operando) y el divisor (segundo operando) son iguales o diferentes. Esto determinara el signo del cociente. Inicializar el cociente en cero. 2. Substraer el divisor del dividendo utilizando suma en complemento a 2 para obtener el primer residuo parcial y sumar 1 al cociente. Si el residuo parcial es positivo, ir al paso 3, si es cero o negativo, la división está completa. 3. Substraer el divisor del residuo parcial y añadir 1 al cociente. Si el resultado es positivo , repetir para el siguiente residuo parcial, si el resultado es cero o negativo, la división está completa. Ejemplo: Dividir el número con signo: 01100100 entre 00011001 (8 bits) 1. El signo de ambos números es positivo, por lo tanto el cociente será positivo. El cociente es inicialmente 00000000. 2. Substraer el divisor del dividendo utilizando suma en complemento a 2. (Recuerde: Los carries finales se descartan) 01100100 + 11100111 01001011 Residuo parcial positivo Añadir 1 al cociente: 00000000 + 00000001 = 00000001 3. Substraer el divisor del primer residuo parcial utilizando suma en complemento a 2. 01001011 + 11100111 00110010 Residuo parcial positivo Añadir 1 al cociente: 00000001 + 00000001 = 00000010 4. Substraer el divisor del segundo residuo parcial utilizando suma en complemento a 2. 00110010 + 11100111 00011001 Residuo parcial positivo Añadir 1 al cociente: 00000010 + 00000001 = 00000011 4. Substraer el divisor del tercer residuo parcial utilizando suma en complemento a 2. 00011001 + 11100111 00000000 Residuo cero Añadir 1 al cociente: 00000011 + 00000001 = 00000100 Cociente Final Ejercicios: 1. Realizar las siguientes multiplicaciones de números binarios con signo y verificar en decimal: a. 10101110 x 01000111 b. 00111100 x 10001110 c. 01111111 x 00000101 2. Cual es el signo del producto cuando se multiplican dos números negativos. 3. Cual es el signo del cociente cuando un número positivo se divide entre un número negativo. 4. Divida 00110000 entre 00001100