AUTOCORRELACION
Anuncio
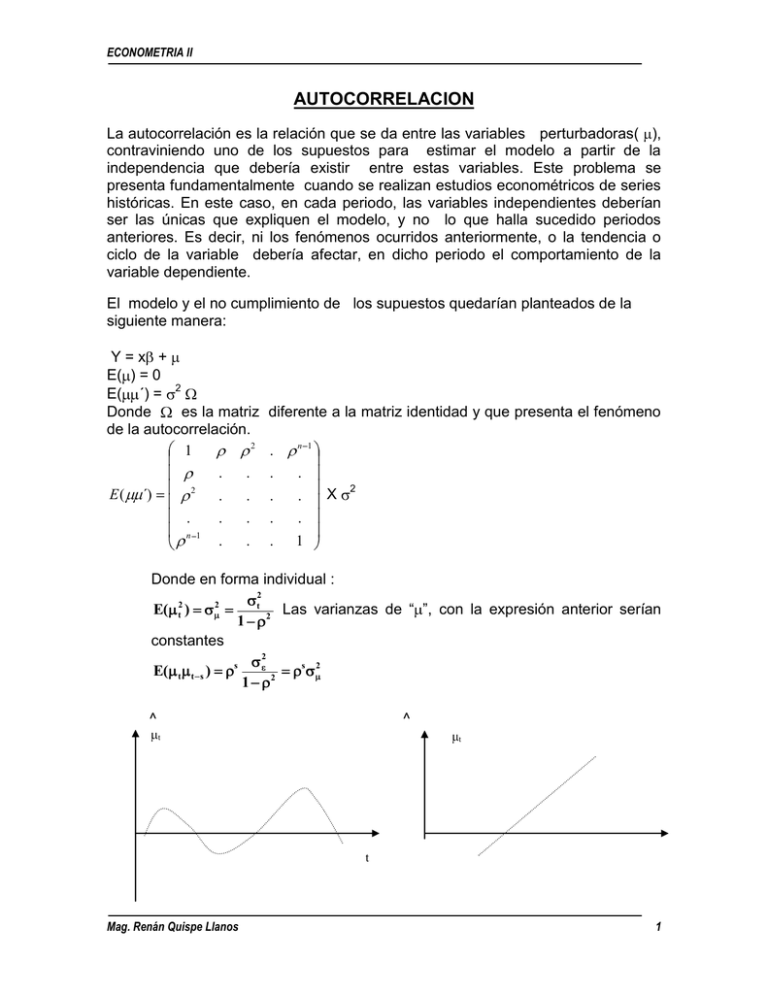
ECONOMETRIA II AUTOCORRELACION La autocorrelación es la relación que se da entre las variables perturbadoras( ), contraviniendo uno de los supuestos para estimar el modelo a partir de la independencia que debería existir entre estas variables. Este problema se presenta fundamentalmente cuando se realizan estudios econométricos de series históricas. En este caso, en cada periodo, las variables independientes deberían ser las únicas que expliquen el modelo, y no lo que halla sucedido periodos anteriores. Es decir, ni los fenómenos ocurridos anteriormente, o la tendencia o ciclo de la variable debería afectar, en dicho periodo el comportamiento de la variable dependiente. El modelo y el no cumplimiento de los supuestos quedarían planteados de la siguiente manera: Y=x + E( ) = 0 E( ´) = 2 Donde es la matriz de la autocorrelación. 2 1 . . 2 E ( ´) . . . . . n 1 . . diferente a la matriz identidad y que presenta el fenómeno . n 1 . . . . . . . 1 X 2 Donde en forma individual : E( 2 t 2 t 2 ) Las varianzas de “ ”, con la expresión anterior serían 2 1 constantes 2 E( t t s) s s 1 2 2 ^ ^ t t t Mag. Renán Quispe Llanos 1 ECONOMETRIA II ^ ^ t ut t t FIGURA. A-1 1. CAUSAS DE LA PROCEDENCIA DE AUTOCORRELACION 1. La inercia de los procesos económicos, quiere decir, la variable debe crecer en el tiempo. 2. El sesgo de especificación, se da cuando se excluye a una variable importante o la forma funcional del modelo no es la correcta. En el primer caso: Y = 1 + 2x2 + 3x3 + , es difícil especializar el fenómeno. 3. Rezagos en los modelos: Ct = 0 + 1y + 2Ct-1 + t Ct-1 = 0 + 1y + 2Ct-2 + t-1 Cuando se habla de rezagos puede haber autocorrelación. 4. Existencia de ciclos y tendencias, si la autocorrelación es positiva, un valor alto de ut genera un valor de yt por encima de su promedio, y en consecuencia una elevada probabilidad de ir seguido de un valor alto de u t+1, y de un valor de yt+1 por encima de su promedio, lo mismo ocurriría para valores de y t por debajo de su promedio. 5. La autocorrelaciòn positiva está asociada a la existencia de rachas de valores altos y bajos de yt. (Fig. A -2 ) 6. El conjunto de variables explicativas del modelo no explican adecuadamente dicho comportamiento, entonces el término de error incorporará dicha tendencia, y esto conduce a la existencia de autocorrelaciòn positiva . Una primera racha de residuos negativos seguida por otra racha de residuos positivos.(Fig A -3) y Modelo verdadero Modelo estimado 2 Mag. Renán Quispe Llanos Modelo Estimado ECONOMETRIA II t FIGURA. A-2. Autocorrelación producida por un ciclo FIGURA. A-3. Autocorrelación producida por una tendencia 7. Manipulación de Datos. En especial cuando se realiza la interpolación y extrapolación de la información. 2. CONSECUENCIAS DE LA AUTOCORRELACION Los estimadores de MCO tendrán las siguientes propiedades: 1. Son insesgados en muestras repetidas sus valores medios son iguales a las verdaderos valores reales. 2. Son consistentes a medida que el tamaño de la muestra se aproxime a los verdaderos valores. 3. Como en el caso de heterocedasticidad ya no son eficientes (mínima varianza) ni para muestras pequeñas ni grandes. a. Aunque se tenga en cuenta la correlación serial en los estimadores mínimos cuadrados ordinarios (MCO) y se utilice la fórmula de varianza con autocorrelación los estimadores serán menos eficientes. En consecuencia los intervalos de confianza son más anchos de lo necesario y la prueba de significancia pierden fuerza. Fórmula de varianza en presencia de autocorrelación 1 2 V( )MCG = Si se ignora el problema de autocorrelación y se aplica la fórmula clásica de MCO (bajo el supuesto de ausencia de correlación) las consecuencias son todavía más serias y la varianza residual tiende a subestimar la varianza verdadera. b. Incluso si la varianza residual estuviera subestimada las varianzas y los errores estándar de los estimadores MCO tienden a subestimar las verdaderas varianzas de los parámetros estimados. c. En consecuencia las pruebas de significancia pierden validez y si se aplica tienden a dar conclusiones erróneas. Yt = 1 + 2xt Mag. Renán Quispe Llanos + t 3 ECONOMETRIA II t = t-1 + (autocorrelación de primer orden) t E( t)=0, E( t2)= donde: t 2 , E( t t+s)=0 La Autocorrelación, será de segundo orden cuando el subíndice sea t-2, y así sucesivamente. Entonces: E( 2 t 2 t 2 ) 2 1 2 E( t t s s) s 2 2 1 Para el modelo general: Y=x + E( ) = 0 E( ´) = 2 2 E( ´) . . . . . . . . . . . . . . 2 1 , entonces: E ( n 2 ´) . n 1 . n 1 . . . . . . . . . . . . . . . 1 3. DETECCION DE AUTOCORRELACION El supuesto de no autocorrelación del modelo clásico se relaciona con las perturbaciones poblacionales t, las cuales no pueden ser observadas directamente. En su lugar, se dispone de sus valores aproximados, los residuales ˆ t que pueden obtenerse a partir del procedimiento usual MCO. Aunque las ˆ t no son lo mismo que las t , con mucha frecuencia un examen visual de las ˆ nos da algunas claves sobre la posible presencia de autocorrelación en las . PRUEBA DE DURBIN WATTSON Se construye la dócima de hipótesis: H0: H1: = 0 (no existe autocorrelación) 0 (existe autocorrelación) Mag. Renán Quispe Llanos 4 ECONOMETRIA II Se utiliza el estadístico de Durbin Wattson: n (e t et 1 )2 t 2 d n e t2 t 2 Desagregando la fórmula: n n (e t e t 1 ) 2 (e t2 2et e t t 2 1 e t2 1 ) e t2 2 etet 1 e t2 1 t 2 Suponiendo que e t-1 = et y reemplazando: d et2 2( et et 1 ) e entonces: ˆ et et 2 t d 2 2 2 1 et et et2 1 2(1 ˆ ) , donde: 1 2 t e Cuando: = -1 =1 =0 d=4 Autocorrelación negativa d=0 Autocorrelación positiva d=2 No existe autocorrelación. DETECCION DE AUTOCORRELACION CUANDO EL MODELO TIENE UNA VARIABLE ENDOGENA REZAGADA Cuando en el modelo se tiene una variable explicativa que esté rezagada, generalmente se refiere a la variable dependiente que esta considerado además como rezagada. En este otro caso, para detectar autocorrelación, el estadístico propuesto por Durbin Watson, es el estadístico h, y se calcula como: Mag. Renán Quispe Llanos 5 ECONOMETRIA II h ˆ n 1 nˆ 2 1 donde: = estimador de la variable endógena rezagada (del primer retardo). Es decir es el coeficiente de Yt 1 en la regresión mínimo-cuadrática (MCO): 1 Yt a1 1t a2 2t Yt 1 1 y ˆ 2 , la estimación de la varianza muestral de 2 Yt 1 2 ..... u t . 1 Es utilizable sólo para n ˆ 2 1 1 , siendo el coeficiente estimado de autocorrelación de primer orden de los residuos ( ), calculable a partir del valor de 1 d : ˆ 1- d 2 El contraste de h se realiza a partir de su consideración de variable distribuida normalmente con parámetros (0,1). Así, con un nivel de significación del 5 por 100, si h 1,645 debe rechazarse la hipótesis de autocorrelación nula (ver figura). Ejemplo: Sea d = 1.75, n = 25, ˆ 0.15 . Hallar h 1 ˆ 1 1 d 2 1 1 (1.75) 2 Mag. Renán Quispe Llanos 0.125 6 ECONOMETRIA II Entonces: h 0.125 25 1 25(0.0225) 0.945 Luego, para un nivel de significancia del 5%, tenemos: Como h = 0,945 y no se cumple la desigualdad, h 1,645 , no tenemos evidencias para rechazar la hipótesis nula de ausencia de autocorrelación. Una extensión inmediata del contraste de DW ha sido realizada por Wallis (1972) para el caso de un proceso autorregresivo de cuarto orden, pero con un único parámetro no nulo en μt-4: t 4 t 4 t La justificación del contraste de Wallis está en la utilización de datos trimestrales en la estimación del modelo, en cuyo caso puede resultar más probable una correlación serial entre trimestres iguales de años sucesivos, por ejemplo por la omisión de variables con efectos estacionales relevantes. CONTRASTE DE AUTOCORRELACION EN BASE AL MULTIPLICADOR DE LAGRANGE (LM) El procedimiento del multiplicador de Lagrange es usado para la detección de autocorrelación entre los residuos de una ecuación. El contraste es adecuado para los casos de indeterminación al usar el estadístico “d” de Durbin-Watson, o de imposibilidad de obtención para el h de Durbin1. Sin embargo, es importante señalar que su uso no debe limitarse a dichos casos. El contraste LM para trabajar se debiera aplicar como complemento a los demás, y se aplica con una variable aleatoria (LM) que se debe trabajar como X2. LM X 21 1 grado de Libertad ó 1 Sin embargo, es importante que el lector no interprete que su uso se limita a dichos casos. El contraste LM se puede (y debe quizás aplicar como complemento a los demás. Mag. Renán Quispe Llanos 7 ECONOMETRIA II X2 LM grados de Libertad El procedimiento consta de las siguientes etapas, para el caso de autocorrelación de primer orden: 1o Regresión de la ecuación original por MCO: Yt 1X1t 0 2X2 t ...... k Xkt t Estimación del término de perturbación a partir del cálculo de los residuos ( e t ). et t ˆt 2 o Regresión de los residuos de la ecuación en función de las variables explicativas y de los residuales con un período de rezago: et 1X1t ...... k X kt 1e t 1 vt 2 3º Obtención del R de la regresión y cálculo del estadístico de prueba para la autocorrelación de primer orden: LM = n R 2 Donde n es el tamaño muestral. El estadístico LM sigue aproximadamente una distribución normal con 1 grado de libertad (en casos de contraste de autocorrelación de primer orden). LM X 21 Sin embargo, su uso no se limita a dichos casos. El contraste LM se debiera aplicar como complemento a los demás. La regla de decisión es: Si LM > X 2 crítico – Existe autocorrelación significativa de primer orden. Si LM < X 2 crítico – No existe autocorrelación significativa de primer orden. El contraste en base al multilplicador de Lagrange puede usarse igualmente para la detección de autocorrelación de orden p en los residuos de una ecuación. Para tales efectos, luego de estimar los residuos de la ecuación, se debe aplicar la siguiente fórmula: et Mag. Renán Quispe Llanos 1X1t ...... k X kt 1e t 1 ...... 1e t p wt 8 ECONOMETRIA II para obtener el coeficiente de determinación ( R 2 ). El estadístico de prueba es: n R 2 donde LM X2p regla de decisión es: Si LM > X 2 crítico – Existe autocorrelación significativa de orden p. Si LM < X 2 crítico – No existe autocorrelación significativa de orden p. “Contraste en base al Multiplicador de Lagrange” JJ THOMAS, utiliza un esquema incorporado de hipótesis. Harvey (1981) demostró que en muestras pequeñas, el contraste de LM pierde confiabilidad, maximizando la probabilidad de ocurrencia de errores tipo y propone la siguiente modificación: LM n k R2 p 1 R2 F(p,n-k) El estadístico LM puede utilizarse igualmente para el contraste de la autocorrelación para p mayor de grado. EL CONTRASTE DE BOX- PIERCE Sea s el coeficiente de autocorrelación de e t y et 1 , siendo s = 1, 2, 3,....., . Sera Q el estadistístico de prueba de autocorrelación de Box-Pierce, cuya expresión es: p Qp 2 i n X 2 p (para todo i = 1, 2, 3,......,p) 1 Para contrastar autocorrelación de primer orden etet Q1 2 n ˆ1 , siendo 1 ˆ1 e2 t y Q1 X 21 Para contrastar autocorrelación de segundo orden Mag. Renán Quispe Llanos 9 ECONOMETRIA II etet Q2 n 2 1 2 2 2 siendo ˆ e2 t y Q2 X 22 para contrastar autocorrelación de orden p etet Qp n 2 1 2 2 .... 2 2 p siendo ˆ p e2 t Mag. Renán Quispe Llanos 10 ECONOMETRIA II EL CONTRASTE DE LJUNG Y BOX Cuando se trabaja con muestras pequeñas se han detectado algunas irregularidades. Para esos casos, Ljung y Box (1978) demostraron que la consideración de los grados de libertad producen un contraste adecuado, resultando el siguiente estadístico: 1 Q nn 2 ˆ 2s n s 1 En ambos casos , la hipótesis de autocorrelación significativa de orden m es aceptada si el valor calculado del estadístico supera al valor crítico de la tabla con m grados de libertad. Q* X 2 1 p Qp n 1 ˆ i2 nn 2 X 2p 1 Para todo i = 1, 2, 3, ....,p. Entonces Q1 Q nn 2 nn 2 2 2 1 X 21 n 1 2 1 2 2 n 1 n 2 X 22 Autocorrelación de orden p Q donde 1, 2 ,..... p p nn 2 2 1 2 n 1 n 2 2 2 ..... p n p X 2p son los coeficientes de autocorrelación de orden 1,2 y p, cuyas expresiones son conocidas. Un aspecto importante, es que los estadísticos de contraste Box-Pierce y Box-Ljung detectan el grado de autocorrelación de orden p, de manera discontinua. Esto permite afirmar que si por ejemplo 4 es significativamente elevado eso no implica que ˆ 1 , ˆ 2 y ˆ 3 también lo sean, a no ser que de manera complementaria se demuestre lo contrario. Mag. Renán Quispe Llanos 11 ECONOMETRIA II MODELO AUTORREGRESIVO DE HETEROSCEDASTICIDAD CONDICIONAL (ARCH) Se ha determinado que el problema de autocorrelación es una característica de la información de series de tiempo y la heteroscedasticidad una característica de la información de corte transversal. No obstante, se ha observado que para predecir variables financieras varía considerablemente de un periodo de tiempo a otro. Para algunos períodos de tiempo, los errores de proyección son relativamente pequeños, durante otros, ellos pueden ser relativamente grandes. Esta variabilidad podría deberse a la volatilidad en los mercados financieros, esto sugeriría que la varianza de los errores de predicción no es constante sino que varía de un periodo a otro. En consecuencia, se puede afirmar que los errores de predicción dependen del comportamiento de las perturbaciones t. Puede presentarse una situación de autocorrelación en la varianza t. Para captar esta correlación, Engle desarrolló el modelo autorregresivo de heterocesdasticidad condicional (ARCH). La idea central el ARCH es que la varianza de en el tiempo t (= 2t), depende del tamaño del término del error al cuadrado en el tiempo (t-1), es decir, de 2 t-1. Tenemos el modelo de regresión con k variables : Yt x 1 2 2t 3 x3t ...... x k kt ...... ( 1 ) t supóngase que condicional a la información disponible en el tiempo (t-1), el termino de perturbación se distribuye así: t ~ N [0,( 0 + 1 2 t-1) ] ........ ( 2) Lo nuevo aquí es la varianza de en el tiempo t depende de la perturbación al cuadrado en el tiempo (t-1), dando así la apariencia de correlación serial. El proceso se denomina ARCH(1). Pero éste se puede generalizar fácilmente. Es así como el proceso ARCH(p) puede escribirse como: Var( t) = 2 t = 0 + 1 2 t-1 + 2 2 t-2 + ....+ 2 p t-p ........(3) A fin de verificar la no existencia de correlación entre las varianzas de los términos de perturbación, se realiza la siguiente dócima: Si Ho : error. 1 = 2 = .....= p = 0, en cuyo caso Var( t) = 0 varianza homoscedástica del Se puede realizar una prueba sobre la hipótesis nula anterior efectuando la siguiente regresión: ^ Mag. Renán Quispe Llanos ^ ^ ^ ^ ^ ^ ^ 12 ECONOMETRIA II 2 t donde t, = 0 + 1 2 t-1 + 2 2 t-2 + ....+ p 2 t-p ......... (4) denota los residuales MCO estimados del modelo de regresión original (1). Calculando el nR2, donde R2 es el coeficiente de determinación obtenido en la regresion auxiliar (4) puede demostrarse que: nR2 ~ X2p ..........(5) donde p es el número de grados de libertad y equivale al grado de autocorrelación. Si el estadístico contenido nR2 es mayor que el X2p se aceptaría que existe correlación entre las varianzas del término de perturbación. EJEMPLO ILUSTRATIVO Sobre salarios y productividad. Utilizando los residuales obtenidos de esta regresión, se estiman los modelos ARCH(1), ARCH(2), ARCH(3), ARCH(4), ARCH(5). Pero solamente el modelo ARCH(1) resultó ser significativo. Los resultados de este modelo resultó ser el siguiente: 2 t = 2.0746 + 0.6946 t = (1.0583) 2 t-1 (5.03649) R2 = 0.4665 d = 1.67 aplicando (5) se observa que nR2 = (31)(0.4665) = 14.46 que es aproximadamente X2 con 1 g.l. (el valor p es alrededor de 0.000143) esto sugiere que en el ejemplo, la varianza del error está correlacionada serialmente. REVISADO Mag. Renán Quispe Llanos 13 ECONOMETRIA II Mag. Renán Quispe Llanos 14

![[ ] ε](http://s2.studylib.es/store/data/004599547_1-2f20235d60ac9bc80564c7074e516da7-300x300.png)

