Diversas experiencias con partículas α

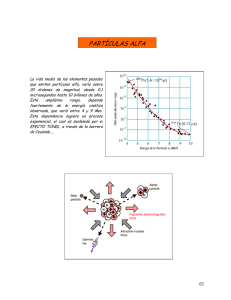
Diversas experiencias con partículas α
Física Nuclear y de Partículas
INTRODUCCIÓN
La pérdida de energía por unidad de longitud (poder de frenado) de una partícula cargada,
caracterizada por su carga z y su velocidad β=v/c, en un medio material (definido por los
parámetros Z, A, ρ e I) está determinada por la ecuación de Bethe-Bloch1. En el caso de iones
pesados esta pérdida de energía se debe primordialmente a interacciones de tipo atómico, lo que da
lugar a una dependencia lineal en el número atómico Z del medio material:
−
e 4 N A ρZ z 2
dE
=
dx 4πε 02 m0 A β 2
 2m c 2 β 2

×  ln 0
− ln(1 − β 2 ) − β 2 
I


Por tanto el poder de frenado de un material dado puede medirse haciendo pasar partículas de
carga z y energía (velocidad) conocida (β=v/c) a través de una lámina de dicho material de espesor
conocido y midiendo la energía de las partículas después de atravesarla. Alternativamente, si el
poder de frenado de un material es conocido, el espectro de energía de partículas cargadas tras su
paso por una lámina de este material proporciona información sobre el espesor de la misma. En
particular es posible utilizar partículas α (z=2) emitidas por una fuente de espectro de energías
conocido y determinar la atenuación que sufren a su paso por un material. Éste es el fundamento de
la práctica. Para realizar las medidas dispondremos de fuentes α, diversos materiales, y un detector
conectado a un sistema de toma de datos que permite medir espectros α.
En el caso de que el material fuera gaseoso el procedimiento básico para determinar la
atenuación consistiría en introducir la fuente de partículas α en el gas e ir modificando
progresivamente la distancia de la fuente con relación al detector (x), contando el número de
partículas que inciden en éste en un tiempo dado. Sin embargo, para evitar posibles errores debidos
a la diferente geometría y la dirección de incidencia de las partículas α en el detector, un
procedimiento alternativo consiste en situar la fuente a una distancia fija del detector d y modificar
la presión del gas P. La expresión
x=d×
P
Pa
relaciona la distancia x a la cual ocurriría la misma pérdida de energía que a la presión atmosférica
Pa con la distancia d y la presión medida P. Así pues, variando la presión y estudiando el espectro
obtenido para cada valor, se puede obtener la relación entre la energía de las partículas que
alcanzan el detector en función de la presión, y por tanto de la distancia x a presión constante. De
dE
esta relación se obtiene también −
.
dx
1
K.S. Krane, Introductory Nuclear Physics, John Wiley (1988).
2
MÉTODO EXPERIMENTAL
Descripción de los componentes
Los objetivos de la práctica son la determinación de diversos espectros α con un analizador
monocanal (SCA), con un analizador multicanal (MCA) y con una tarjeta digitalizadora conectada
a un PC. Se pretende además medir las pérdidas de energía de partículas α en aire y en distintos
materiales sólidos. La práctica consta del montaje descrito en las notas de laboratorio que permite
determinar espectros α mediante el uso de detectores de Silicio de barrera de superficie2.
El dispositivo experimental consta de un detector alimentado por una tensión de –12 V de un
preamplificador enchufado a la conexión BIAS. Las señales del detector se extraen a través de la
conexión DETECTOR del preamplificador, y a la salida del este último se conecta un analizador
de amplitud de impulsos CASSY conectado a una tarjeta digitalizadora en un PC con la que se
extraen las señales de voltaje y número de impulsos, lo que permite automatizar la toma de datos
(programa CassyLab). Alternativamente se puede conectar la salida del detector al analizador de
impulsos del sistema, que opera como un analizador monocanal (SCA). Con él se puede hacer un
barrido de amplitudes (voltajes) a intervalos constantes (100, 200 o 500 mV) o proporcionales (1%,
2%, 5%). Acoplándolo a un Contador P se determina el número de cuentas en un intervalo de
tiempo dado. El SCA dispone también de una salida de amplitud (OUT OSCILOSCOPE) que
puede utilizarse para visualizar las señales en un osciloscopio.
Las medidas se realizan en un recipiente cilíndrico de vidrio, en el que se encuentra el detector
de Si de barrera de superficie, y en el que se introducen las fuentes α y, en su caso, las láminas de
diversos materiales. Se hace vacío mediante una bomba de aceite; el vacío se mide con una sonda
de presión de tipo Piranni cuya salida de voltaje se lee con la tarjeta digitalizadora (programa Pico).
El programa de toma de datos del ordenador realiza directamente la conversión entre el voltaje
medido (V) y la presión (mbar).3
OBJETIVOS DE LA PRÁCTICA
Medida del espectro del
210
Po. Calibración.
La fuente de 210Po es una fuente abierta (no encapsulada) que tiene un pico conocido, cuya
energía es de 5.30 MeV4. Suponiendo que la ordenada en el origen es nula (energía 0 corresponde
a voltaje 0) se puede obtener una calibración lineal (E = a × V + b) del sistema experimental de
medida.
La fuente de 210Po está contenida en el recipiente del montaje experimental. Se pone en
marcha la bomba y se hace vacío hasta alcanzar un valor inferior a 3.0 mbar. Se desconecta la
bomba manteniendo la válvula cerrada y se espera hasta que el valor de presión se estabilice. El
procedimiento lleva entre 5 y 10 minutos.
2
W. Leo, Techniques for Nuclear and Particle Physics Experiments, Springer Verlag (1987).
En el caso de aplicar voltajes inversos al detector entre -15 y -100 V debe evitarse trabajar en la zona marcada en rojo.
4
E. Lehderer y C. Shirley, Table of Isotopes. WWW: nucleardata.nuclear.lu.se.
3
Diversas experiencias con partículas α
3
Se aplica tensión al detector y se conecta la salida al dispositivo CASSY con la tarjeta
digitalizadora. Iniciando la adquisición de datos en el ordenador se obtiene el espectro de la fuente.
Σx y
El espectro obtenido en el ordenador ha de caracterizarse determinando el centroide ( x = i i ) y
Σxi
210
la anchura a media altura (FWHM) del pico de Po que aparece, para posteriormente poder
calibrar. Se debe hallar también el número de cuentas en el pico por unidad de tiempo. Se puede
incluir la calibración en los espectros empleando la función del programa CassyLab Alt+E.
Medida de la atenuación de las partículas α en aire
Sin modificar el dispositivo experimental se ha de obtener el pico de 210Po a distintas
presiones. La finalidad es obtener el poder de frenado a partir de los datos experimentales y
comparar con los datos tabulados. Es necesario conocer la distancia d a la que se encuentra la
fuente de polonio. Para ello se comprueba que se mantiene el vacío en el recipiente con presión en
torno a los 3.0 mbar. Esta presión equivaldría a una distancia muy pequeña a presión atmosférica
(Pa = 1013 mbar), a la que podemos hacer corresponder el origen de distancias x.
Posteriormente se varia progresivamente la presión abriendo muy suavemente la válvula del
recipiente hasta tener la serie de valores de presión 50, 100, 150, 200, 300, 400, 500, 600, 700 y
800 mbar (9 valores más). Para cada presión se obtiene el espectro de energía empleando el
programa de ordenador. Los espectros resultantes se han de almacenar para su posterior
tratamiento. Se recomienda emplear ficheros.txt, fácilmente legibles por una amplia gama de
programas. El programa es capaz de almacenar todos los valores tomados en un mismo fichero de
texto, pero es conveniente guardar los datos con cierta frecuencia.
A partir de los espectros experimentales se obtiene la energía del pico de 210Po en función de
dE
. Se emplea la tabla de poder de frenado y rango de
la distancia x, y a partir de estos datos −
dx
partículas alfa en aire para comparar las pérdidas de energía y el rango de partículas α en función
del espesor, y por tanto de la presión. La tabla figura en el Apéndice I y corresponde a la salida del
programa SRIM para entorno Windows, que también está disponible en el PC para su uso.
Medida del espectro de
226
Ra
Se trata de obtener el espectro de la fuente de 226Ra en vacío, para después poder comparar con
los espectros obtenidos al atravesar un medio material. Para ello se emplea también la tarjeta
multicanal digitalizadora. Los picos de energía de la fuente de 226Ra no sólo son debidos a la
desintegración del núcleo 226Ra sino también a cada uno de sus sucesores, por lo que será necesario
identificar los picos del espectro.
Se introduce la fuente de 226Ra en el recipiente y se aproxima al detector a una distancia
conocida d cuidando que en ningún caso lo toque. Tras cerrar el recipiente se pone en marcha la
bomba y se hace vacío hasta alcanzar una presión inferior a 3.0 mbar. Se puede cerrar entonces la
válvula de salida del recipiente y desconectar la bomba. Se mide entonces el espectro de 226Ra y se
caracterizan sus picos de la misma forma que para la fuente de Polonio
Medida de la atenuación de las partículas α en aire
Se repite el procedimiento empleado para el 210Po con la fuente de 226Ra. Los valores de presión en
este caso pueden reducirse a 6, incluyendo 100, 200, 400, y 700 mbar. Como el sistema está ya
Diversas experiencias con partículas α
4
calibrado utilizando el pico del 210Po se puede obtener la energía de los picos de la fuente de 226Ra
y comparar con los valores de la literatura. Se procede de la misma manera que con el 210Po para
determinar la atenuación de las partículas α en aire, obteniendo la energía en función de la
dE
distancia y el poder de frenado −
.
dx
Medida de la atenuación de las partículas α en materiales
Se emplea el analizador multicanal para determinar la perdida de energía de las partículas α de
la fuente de 226Ra a su paso por láminas de oro y aluminio de espesor desconocido. Se abre el
recipiente y se inserta la lámina de aluminio entre el detector y la fuente, con cuidado de no tocarla.
Se hace vacío de nuevo y se repite el mismo procedimiento de medida con la tarjeta digitalizadora
que el empleado anteriormente. Se determina así el número de cuentas por unidad de tiempo, y la
posición y anchura de los picos del espectro.
El mismo procedimiento se repite con la lámina de pan de oro. Debido a su extrema fragilidad, el
diafragma en el que está colocado debe manejarse con delicadeza.
Se emplean las tablas de poder de frenado y rangos de partículas alfa en aluminio y oro para
comparar las pérdidas de energía y el rango de partículas α en función del espesor de las láminas.
Estas tablas aparecen en los Apéndices II y III, respectivamente.
Operativo opcional
Comprobación de los espectros con el SCA
Se conecta la salida del detector a la entrada del módulo SCA (ver las notas de laboratorio) y se
acopla el Contador P para poder determinar el número de cuentas por unidad de tiempo.
Empleando la amplificación 2 del SCA y la ventana de 500 mV se procede a hacer un barrido de
500 mV en 500 mV comenzando en 0 mV y acumulando cuentas durante 30 s, que se miden con el
cronómetro proporcionado al efecto. Para ello se puede usar la fuente de 226Ra con o sin lámina de
oro, o bien remplazar la fuente por la de 210Po. La lectura de voltaje la proporciona directamente el
programa Pico del ordenador5. Empleando el barrido automático se puede observar en qué zonas
existen picos de energía en el espectro. Esta región, que comprende aproximadamente 3 V para la
fuente de 226Ra, se explora con mayor detalle utilizando una ventana de 100 mV y un barrido
manual de 100 mV, lo que permite obtener el espectro de la fuente, determinando el número de
cuentas para cada intervalo de voltaje durante unos 30 s.
Empleando el programa Pico del PC, y realizando un barrido automático de voltajes de intervalo
0.8 segundos y con una ventana de 200 mV se obtiene el espectro en el ordenador, y se compara
con los obtenidos anteriormente. Ha de colocarse el selector manual (que se ha estado
manipulando en el punto anterior) en el valor máximo de voltaje que se desea alcanzar en el
barrido.
5
Es aconsejable observar previamente las señales de amplitud en el osciloscopio.
Diversas experiencias con partículas α
5
RESULTADOS EXPERIMENTALES
1. Representar los espectros obtenidos con el ordenador de 210Po y 226Ra con los datos
experimentales y su error estadístico (barras de error en y). Caracterizarlos determinando el
centroide y la anchura a la media altura (FWHM) de los picos. Si fuera preciso, efectuar un
ajuste gaussiano de los mismos.
a. opcional En el caso del 226Ra, hacerlo también para el espectro manual obtenido
con el analizador de amplitud de impulsos (SCA) y compararlo con el del ordenador.
2. Calibrar los espectros con los datos obtenidos para la fuente de 210Po a la presión más baja.
Comparar las energías obtenidas para los picos del espectro de la fuente de 226Ra con los de
la literatura, y valorar si se trata de una fuente encapsulada o no.
3. Caracterizar cada uno de los espectros de la fuente de 210Po obtenidos en función de la
presión, determinando la energía (E), su incertidumbre y la anchura (FWHM) de los picos.
Analizar el comportamiento de la energía a medida que aumenta la presión.
dE
) en
dx
función de la distancia, con sus correspondientes incertidumbres. Estimar la pérdida de
energía por unidad de longitud y el alcance las partículas α (de esta energía) en aire.
4. Obtener y representar la energía media (E) y la pérdida diferencial de energía ( −
5. Evaluar cualitativamente los resultados obtenidos con la fórmula de Bethe para el poder de
frenado y comparar con los resultados experimentales.
6. Comparar los resultados con los obtenidos mediante cálculos Monte Carlo con el programa
SRIM para partículas α incidiendo en aire (Apéndice I).
7. Caracterizar cada uno de los espectros obtenidos con los dos materiales entre el emisor α y
el detector, determinando la energía (E) y anchura (FWHM) de los picos. Determinar
también el número de cuentas por minuto en el pico de energía superior para cada uno de
los espectros.
8. Utilizando las tablas de los Apéndices II y III, y/o el programa SRIM de cálculos Monte
Carlo de interacción radiación-materia en entorno Windows estimar el grosor de cada una
de las láminas (oro y aluminio) utilizadas.
9. Evaluar los resultados obtenidos con la fórmula de Bethe, conocida la densidad, el número
másico y el atómico de cada material, y el espesor de las láminas. Comparar con las
simulaciones SRIM y con los datos experimentales.
CUESTIONES
1.
Indicar posibles fuentes de error en la determinación de la energía.
2.
¿Es posible medir el fondo de radiación α con el dispositivo experimental?
3.
Con los montajes experimentales disponibles, ¿cómo se podría
experimentalmente la dependencia del número de cuentas con el ángulo sólido?
verificar
Diversas experiencias con partículas α
6
Direcciones útiles para la realización de la práctica
Buscar una desintegración radioactiva
http://nucleardata.nuclear.lu.se/database/nudat
(Se puede buscar el Radio y seguir su serie de desintegración)
Entrada general a la base de datos anterior
http://nucleardata.nuclear.lu.se/database/
Una introducción a las series radioactivas
http://www.rwc.uc.edu/koehler/biophys/7c.html
Experimento de Rutherford
http://library.thinkquest.org/19662/low/eng/exp-rutherford.html
Diversas experiencias con partículas α
7
APÉNDICE 1
Poder de frenado de partículas α en aire
Target = Air (gas)
Density = 1,3000E-03 g/cm3 = 5,2873E+19 atoms/cm3
Target Composition
Atom
Atomic
Numb
Percent
O
8
023,20
N
7
075,50
Ar
18
001,30
I (Bethe parameter) = 86 eV
Ion = Helium [2] , Mass = 4,003 amu
Stopping Units = keV / µm
Atom Name
Ion Energy
500,00 keV
600,00 keV
700,00 keV
800,00 keV
900,00 keV
1,00 MeV
1,20 MeV
1,40 MeV
1,60 MeV
1,80 MeV
2,00 MeV
2,25 MeV
2,50 MeV
2,75 MeV
3,00 MeV
3,50 MeV
4,00 MeV
4,50 MeV
5,00 MeV
5,50 MeV
6,00 MeV
7,00 MeV
8,00 MeV
9,00 MeV
10,00 MeV
dE/dx Elec.
dE/dx Nuclear
2,535E-01
2,575E-01
2,569E-01
2,533E-01
2,480E-01
2,416E-01
2,275E-01
2,134E-01
2,002E-01
1,882E-01
1,775E-01
1,657E-01
1,554E-01
1,464E-01
1,385E-01
1,252E-01
1,146E-01
1,052E-01
9,803E-02
9,190E-02
8,657E-02
7,776E-02
7,075E-02
6,501E-02
6,022E-02
4,710E-04
4,050E-04
3,562E-04
3,186E-04
2,886E-04
2,641E-04
2,263E-04
1,985E-04
1,771E-04
1,602E-04
1,463E-04
1,322E-04
1,207E-04
1,112E-04
1,031E-04
9,017E-05
8,026E-05
7,242E-05
6,604E-05
6,075E-05
5,628E-05
4,914E-05
4,368E-05
3,936E-05
3,586E-05
Mass Percent
025,07
071,42
003,51
Projected
Range
3,04 mm
3,43 mm
3,81 mm
4,21 mm
4,60 mm
5,01 mm
5,86 mm
6,77 mm
7,73 mm
8,76 mm
9,85 mm
11,31 mm
12,86 mm
14,52 mm
16,27 mm
20,07 mm
24,24 mm
28,79 mm
33,71 mm
38,97 mm
44,57 mm
56,76 mm
70,23 mm
84,97 mm
100,93 mm
Ionization
Potencial (V)
13,618
14,534
15,759
Longitudinal
Straggling
239,41 µm
245,16 µm
250,49 µm
258,56 µm
266,53 µm
274,53 µm
290,96 µm
308,27 µm
326,66 µm
346,22 µm
382,83 µm
439,18 µm
495,78 µm
552,92 µm
610,76 µm
728,84 µm
850,27µm
1,08 mm
1,29 mm
1,50 mm
1,71 mm
2,12 mm
2,87 mm
3,57 mm
4,25 mm
Lateral
Straggling
305,43 µm
314,17 µm
321,99 µm
329,26 µm
336,19 µm
342,94 µm
356,25 µm
369,72 µm
383,68 µm
398,32 µm
413,79 µm
434,45 µm
456,69 µm
480,61 µm
506,24 µm
562,73 µm
626,16 µm
696,59 µm
773,80 µm
857,29 µm
946,78 µm
1,14 mm
1,36 mm
1,60 mm
1,86 mm
Diversas experiencias con partículas α
8
APÉNDICE 2
Poder de frenado de partículas α en Al
Target = Aluminum
Density = 2,7020E+00 g/cm3 = 6,0305E+22 atoms/cm3
I (Bethe parameter) ~ 163 eV
Ion = Helium [2], Mass = 4,003 amu
Stopping Units = keV / µm
Ion Energy
500,00 keV
600,00 keV
700,00 keV
800,00 keV
900,00 keV
1,00 MeV
1,10 MeV
1,20 MeV
1,30 MeV
1,40 MeV
1,50 MeV
1,60 MeV
1,70 MeV
1,80 MeV
2,00 MeV
2,25 MeV
2,50 MeV
2,75 MeV
3,00 MeV
3,25 MeV
3,50 MeV
3,75 MeV
4,00 MeV
4,50 MeV
5,00 MeV
5,50 MeV
6,00 MeV
6,50 MeV
7,00 MeV
8,00 MeV
9,00 MeV
10,00 MeV
dE/dx Elec.
3,349E+02
3,345E+02
3,328E+02
3,301E+02
3,265E+02
3,222E+02
3,173E+02
3,121E+02
3,066E+02
3,009E+02
2,951E+02
2,893E+02
2,835E+02
2,778E+02
2,667E+02
2,536E+02
2,415E+02
2,304E+02
2,202E+02
2,109E+02
2,024E+02
1,946E+02
1,874E+02
1,761E+02
1,645E+02
1,546E+02
1,459E+02
1,382E+02
1,314E+02
1,199E+02
1,104E+02
1,025E+02
Diversas experiencias con partículas α
dE/dx Nuclear
8,301E-01
7,161E-01
6,315E-01
5,660E-01
5,136E-01
4,707E-01
4,349E-01
4,044E-01
3,783E-01
3,555E-01
3,355E-01
3,177E-01
3,019E-01
2,877E-01
2,631E-01
2,381E-01
2,176E-01
2,006E-01
1,862E-01
1,739E-01
1,631E-01
1,537E-01
1,454E-01
1,314E-01
1,199E-01
1,104E-01
1,023E-01
9,545E-02
8,948E-02
7,962E-02
7,182E-02
6,547E-02
Projected
Range
1,84 µm
2,14 µm
2,43 µm
2,73 µm
3,04 µm
3,34 µm
3,65 µm
3,97 µm
4,29 µm
4,62 µm
4,95 µm
5,29 µm
5,64 µm
5,99 µm
6,73 µm
7,68 µm
8,69 µm
9,75 µm
10,85 µm
12,01 µm
13,22 µm
14,47 µm
15,78 µm
18,53 µm
21,46 µm
24,59 µm
27,91 µm
31,43 µm
35,13 µm
43,08 µm
51,76 µm
61,15 µm
Longitudinal
Straggling
1700 Å
1764 Å
1823 Å
1903 Å
1981 Å
2056 Å
2130 Å
2203 Å
2275 Å
2348 Å
2420 Å
2494 Å
2567 Å
2641 Å
2886 Å
3247 Å
3603 Å
3959 Å
4315 Å
4674 Å
5037 Å
5402 Å
5772 Å
7072 Å
8312 Å
9534 Å
1,08 µm
1,20 µm
1,32 µm
1,76 µm
2,17 µm
2,57 µm
Lateral
Straggling
2130 Å
2240 Å
2343 Å
2441 Å
2536 Å
2629 Å
2719 Å
2809 Å
2899 Å
2988 Å
3077 Å
3167 Å
3257 Å
3348 Å
3534 Å
3772 Å
4019 Å
4275 Å
4541 Å
4817 Å
5104 Å
5402 Å
5710 Å
6355 Å
7041 Å
7769 Å
8539 Å
9350 Å
1,02 µm
1,20 µm
1,40 µm
1,61 µm
9
APÉNDICE 3
Poder de frenado de partículas α en Au
Target = Gold
Density = 1,9311E+01 g/cm3 = 5,9040E+22 atoms/cm3
I (Bethe parameter) ~ 797 eV
Ion = Helium [2], Mass = 4,003 amu
Stopping Units = keV / µm
Ion Energy
500,00 keV
600,00 keV
700,00 keV
800,00 keV
900,00 keV
1,00 MeV
1,10 MeV
1,20 MeV
1,30 MeV
1,40 MeV
1,50 MeV
1,60 MeV
1,70 MeV
1,80 MeV
2,00 MeV
2,25 MeV
2,50 MeV
2,75 MeV
3,00 MeV
3,25 MeV
3,50 MeV
3,75 MeV
4,00 MeV
4,50 MeV
5,00 MeV
5,50 MeV
6,00 MeV
6,50 MeV
7,00 MeV
8,00 MeV
9,00 MeV
10,00 MeV
dE/dx Elec.
dE/dx Nuclear
6,385E+02
6,781E+02
7,055E+02
7,227E+02
7,319E+02
7,349E+02
7,334E+02
7,285E+02
7,213E+02
7,125E+02
7,027E+02
6,923E+02
6,815E+02
6,707E+02
6,495E+02
6,243E+02
6,011E+02
5,801E+02
5,609E+02
5,434E+02
5,274E+02
5,127E+02
4,992E+02
4,685E+02
4,495E+02
4,317E+02
4,152E+02
4,000E+02
3,860E+02
3,612E+02
3,399E+02
3,214E+02
2,564E+00
2,255E+00
2,019E+00
1,832E+00
1,680E+00
1,554E+00
1,447E+00
1,355E+00
1,275E+00
1,205E+00
1,143E+00
1,087E+00
1,038E+00
9,925E-01
9,142E-01
8,334E-01
7,668E-01
7,109E-01
6,632E-01
6,220E-01
5,860E-01
5,542E-01
5,260E-01
4,780E-01
4,386E-01
4,056E-01
3,775E-01
3,534E-01
3,324E-01
2,975E-01
2,696E-01
2,468E-01
Projected
Range
8769 Å
1,01 µm
1,14 µm
1,27 µm
1,40 µm
1,53 µm
1,66 µm
1,79 µm
1,92 µm
2,05 µm
2,19 µm
2,32 µm
2,46 µm
2,61 µm
2,90 µm
3,28 µm
3,67 µm
4,09 µm
4,51 µm
4,95 µm
5,41 µm
5,88 µm
6,36 µm
7,38 µm
8,45 µm
9,56 µm
10,72 µm
11,93 µm
13,18 µm
15,82 µm
18,63 µm
21,61 µm
Longitudinal
Straggling
2600 Å
2725 Å
2831 Å
2926 Å
3011 Å
3090 Å
3164 Å
3234 Å
3302 Å
3368 Å
3432 Å
3496 Å
3558 Å
3620 Å
3754 Å
3927 Å
4102 Å
4279 Å
4458 Å
4639 Å
4824 Å
5011 Å
5202 Å
5682 Å
6172 Å
6667 Å
7168 Å
7677 Å
8193 Å
9606 Å
1,10 µm
1,24 µm
Lateral
Straggling
2679 Å
2881 Å
3059 Å
3222 Å
3374 Å
3517 Å
3655 Å
3789 Å
3921 Å
4050 Å
4178 Å
4305 Å
4432 Å
4560 Å
4816 Å
5140 Å
5470 Å
5807 Å
6151 Å
6503 Å
6863 Å
7230 Å
7605 Å
8382 Å
9193 Å
1,00 µm
1,09 µm
1,18 µm
1,27 µm
1,46 µm
1,66 µm
1,87 µm
Diversas experiencias con partículas α