Levitación de origen cuántico

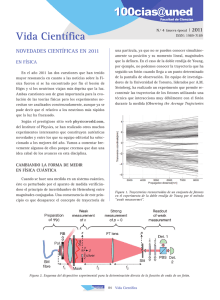
Cinvestav en su tinta
Oscar Rosas-Ortiz*
Levitación de
origen cuántico
Oscar Rosas-Ortiz*
*Investigador titular del Departamento de Física del Centro de Investigaciones y de
Estudios Avanzados (Cinvestav) del Instituto Politécnico Nacional (IPN). Editor de la
presente columna y autor del artículo.
20
Diciembre 2008 - Enero 2009
L
a noción tradicional de vacío como “aquello que no contiene nada” deja de ser útil cuando se investigan fenómenos físicos como el efecto Casimir, que corresponde a la presencia de una fuerza casi imperceptible que actúa entre dos placas conductoras paralelas y
descargadas. Dicha fuerza es atractiva, ha sido medida experimentalmente y su intensidad aumenta cuando la separación entre las placas disminuye. De origen cuántico, el efecto
Casimir se debe a las fluctuaciones de vacío asociadas con los campos electromagnéticos. Las
predicciones teóricas indican que si el vacío se sustituye por el medio apropiado, entonces la
fuerza entre las placas se torna repulsiva.
Tuvieron que pasar cerca de cincuenta años para confirmar experimentalmente esta
última predicción teórica. Los resultados, publicados el pasado 8 de enero, indican que
la fuerza de Casimir repulsiva es mucho más débil que su contraparte atractiva. De esta
forma la levitación cuántica de objetos microscópicos es un fenómeno real y se vislumbra la construcción de nuevos dispositivos en nanotecnología.
En el contexto de la teoría cuántica el vacío no corresponde a un espacio carente de
“cosas”. Muy al contrario, el vacío cuántico está plagado de partículas cuya naturaleza
les permite crearse y aniquilarse a pares en tiempos tan cortos que es prácticamente
imposible detectarlas. Por esta razón dichas partículas reciben el sobrenombre de virtuales. Cada uno de estos pares está compuesto por una partícula y una antipartícula
que se aniquilan mutuamente cuando colisionan una con otra. El proceso de creación
y aniquilación de pares está regulado por el principio de incertidumbre de Heisenberg
y se entiende como una fluctuación del vacío. También en el contexto cuántico, el concepto tradicional de fuerza como una acción a distancia se sustituye por un fenómeno
de intercambio de partículas regulado, nuevamente, por el principio de incertidumbre.
La fuerza electrostática entre dos cargas, por ejemplo, se entiende como el intercambio
de fotones entre ellas (los fotones son las partículas asociadas con los campos electromagnéticos, ver por ejemplo Cruz y Rosas-Ortiz 2008). Como cualquier partícula, los
fotones son portadores de un momento lineal que es adquirido por la carga que los absorbe pero que es perdido por la carga que los emite. La descripción un tanto elaborada
de este proceso en términos de la Electrodinámica Cuántica (la versión cuántica de la
teoría de James Clerk Maxwell que explica, entre otras cosas, el comportamiento de la
luz y de las señales de radio y televisión) permite identificar la naturaleza atractiva o repulsiva de la fuerza con la dirección del momento lineal de los fotones de intercambio.
Un poco de historia
En 1948 el físico Hendrik B.G. Casimir, de los laboratorios de investigación Philips en
Holanda, mostró la relevancia de las fluctuaciones del vacío cuántico asociadas con el
campo electromagnético al predecir un efecto detectable en el mundo macroscópico
(Casimir 1948). Basándose en un trabajo que firmó con Dirk Polder unos meses atrás y
referente a la interacción entre una placa conductora y un átomo (Casimir and Polder
1948), Casimir primero demostró que sus resultados podían obtenerse como un efecto
generado por las variaciones del punto cero de la energía electromagnética (fluctuaciones del vacío cuántico) y después los generalizó al caso de la interacción entre dos placas
conductoras paralelas, separadas entre sí por una distancia a, en ausencia de campo
externo alguno. Desde el punto de vista clásico, si no hay campo externo aplicado tampoco hay campo entre las placas y por lo tanto no debe existir alguna fuerza entre ellas.
Sin embargo, Casimir determinó que asociado con las fluctuaciones de vacío existe un
campo compuesto por ondas cuya longitud es proporcional a la distancia a y encontró
que las placas deberían atraerse una a la otra con una fuerza cuya magnitud es proporcional al inverso de a elevada a la cuarta potencia (es decir, a multiplicada consigo misma cuatro veces). Casimir concluye su artículo con las siguientes palabras: “Esta fuerza
podría interpretarse como una presión del punto cero de las ondas electromagnéticas.
A pesar de ser pequeño, la confirmación experimental de este efecto se antoja viable e
interesante”1 .
IPN
Donde la ciencia se convierte en cultura
21
La predicción teórica del modelo de Casimir tuvo que esperar cerca de 50 años para
verse verificada experimentalmente. La primera aproximación se hizo en 1997 en el Laboratorio Nacional de Los Alamos (E.U.A.) por S.K. Lamoreaux usando una placa plana
y una placa semicircular con radio muy grande (Lamoreaux 1997). La medición con dos
placas planas se hizo usando microresonadores en los laboratorios de la Universidad
de Padua (Italia) por el grupo liderado por G. Bressi hace apenas unos años (Bressi et al
2001).
Un problema por resolver
El trabajo de Casimir fue considerado poco más que una curiosidad teórica durante muchos años, con apenas muy poco beneficio práctico. Sin embargo, con el surgimiento de
la nanotecnología y la creciente necesidad por dispositivos electrónicos cada vez más
pequeños (ver Rosas-Ortiz 2008), en las últimas décadas los tecnólogos y científicos de
todo el mundo han vislumbrado un problema fundamental. A saber: Las dimensiones
de los dispositivos llegan a ser tan pequeñas que la fuerza de Casimir entre sus componentes termina por unirlos entre sí. Para evitar este colapso es necesario entender
cómo se puede contrarrestar dicha fuerza. La opción viable sería la presencia de una
fuerza de la misma naturaleza pero actuando en sentido contrario a la primera. Los
esfuerzos por modelar la presencia de fuerzas de Casimir repulsivas han sugerido que se
debe escoger la geometría de las placas adecuada. Sin embargo, en todos los sistemas investigados experimentalmente con este fin se presentan sólo fuerzas de Casimir atractivas. La pista real que ha llevado finalmente a la solución del problema fue reportada
apenas ocho años después del trabajo de Casimir por Evgeny Lifshitz (Lifshitz 1956). En
el modelo de Lifshitz se incluyen cuerpos macroscópicos tales como sólidos, descritos
por sus funciones de respuesta dieléctrica E, separados por un fluido. Investigaciones
posteriores que incluían líquidos en lugar de sólidos fueron reportados por el mismo
Lifshitz, junto con I.E. Dzyaloshinskii y L.P. Pitaevskii, en 1961. En este último trabajo
se predicen por primera vez las fuerzas de Casimir repulsivas.
Noticias recientes
En un artículo publicado el pasado 8 de Enero en la prestigiosa revista científica Nature,
J.N. Munday, F. Capasso y V.A. Parsegian reportan exitosamente la medición de fuerzas
repulsivas de Casimir de largo alcance (Munday, Capasso and Parsegian 2009). En su
artículo estos investigadores muestran experimentalmente que el signo de la fuerza de
Casimir puede cambiarse de atractivo a repulsivo al escoger los materiales apropiados
inmersos en un fluido, tal y como indica la predicción teórica de Lifshitz y colaboradores. La fuerza repulsiva encontrada resulta ser más débil en intensidad que la fuerza
atractiva. Sin embargo, en ambos casos la fuerza aumenta con el decremento en la distancia de separación. En general, si E(k) es la respuesta dieléctrica del material k, la fuerza será repulsiva si el material 1 y el material 2, junto con el fluido (material 3) tienen
respuestas dieléctricas que satisfacen E(1) < E(3) < E(2). Como material 1 los autores usan
una esfera de polietileno recubierta de oro, el material 2 es una placa plana de oxido de
silicio y como fluido usan bromobenzeno, todos ellos cumplen la condición mencionada
y se consigue una fuerza repulsiva entre las superficies del oro y del oxido de silicio.
El arreglo experimental usado por Munday y colaboradores incluye un microscopio de
fuerza atómica, modificado para detectar fuerzas superficiales promedio más que fuerzas puntuales a escala atómica. La presencia de la superficie de oro esférica antes que
una superficie plana obedece a simplificaciones geométricas del diseño experimental
que evitan la necesidad de alinear dos placas para mantenerlas paralelas. El cambio de
geometría modifica ligeramente la fuerza de Casimir que se desea medir, pero dicha
modificación se puede calcular con suficiente precisión. Más detalles del arreglo experimental y del procedimiento de medición utilizados pueden consultarse en línea
en el portal de la revista (http://www.nature.com/nature/journal/v457/n7226/), que es
de acceso libre. Uno de los aspectos más relevantes de este resultado es que se antoja
posible encontrar el líquido apropiado que produzca una fuerza repulsiva a pequeñas
distancias pero que se torne atractiva para grandes distancias de separación entre las
22
Diciembre 2008 - Enero 2009
superficies. Aquí entendemos por grandes las distancias de separación que sean del orden de las dimensiones de un nano-dispositivo electrónico.
En la definición de diccionario el concepto de levitación se asocia con el “fenómeno
por el que un cuerpo se eleva del suelo y se mantiene así sin ningún apoyo natural”. En
términos más precisos la levitación involucra una fuerza de la misma naturaleza que la
gravitacional pero de sentido opuesto a esta. Así, un cuerpo levitante flotaría a una cierta distancia del suelo. Hasta el momento este tipo de levitación es un asunto de ficción
científica. Hay, sin embargo, casos reales de levitación de otro tipo. Por ejemplo, el efecto
descubierto en 1933 por Walter Meissner y Robert Ochsenfeld consiste en la desaparición total del flujo de campo magnético en el interior de un superconductor a temperaturas por debajo de su temperatura crítica. Dicho efecto se estudia hoy en día como una
práctica de laboratorio avanzado en Física por estudiantes universitarios a lo largo de
todo el planeta, quienes se quedan atónitos al observar directamente la levitación de un
imán como una manifestación de la superconductividad. Como bien se sabe, la diversidad de aplicaciones de esta clase de levitación es bastante amplia e incluye, entre otras,
medios de transporte masivo como el tren de alta velocidad. El reporte presentado en el
artículo de Nature que nos ocupa se incorpora a esta fascinante categoría de fenómenos
físicos tan poco intuitivos y muestra, a su vez, la impresionante solidez de la teoría cuántica. Dicha teoría no ha sido puesta en tela de juicio a lo largo de los casi cien años que
llevamos trabajando con ella y promete todavía muchas sorpresas.
El artículo de Munday, Capasso y Parsegian representa un parte aguas para la tecnología electrónica contemporánea. Como ya indicamos, los resultados que allí se reportan
son una solución viable al inminente colapso de los dispositivos electrónicos cada vez
más pequeños. La levitación cuántica es entonces, no sólo real sino aplicable en el corto
plazo en materiales de pequeñas dimensiones. Para tener una idea del tamaño y las propiedades de esta clase de objetos, el lector puede consultar el artículo de Gabino Torres
Vega sobre osciladores cuánticos (Torres 2008).
De esta forma la nanotecnología ha solventado uno de los principales obstáculos que
podría frenar su desarrollo y, en esta misma línea de pensamiento, se mantienen vigentes los intentos por conseguir un dispositivo de cálculo tan pequeño que opere bajo las
reglas de la física cuántica, es decir, una computadora cuántica.
Referencias
Bressi G., Carugno G., Onofrio R., and Russo G. “Measurement of the Casimir force between parallel metallica surfaces”. Phys. Rev. Lett. 88, 041804. (2002).
Casimir H.B.G. “On the attraction between two perfectly conducting plates”. Proc. Kon. Ned. Akad.
Wetensch B51, 793. (1948).
Casimir H.B.G. and Polder D. “The Influence of Retardation on the London-van der Waals Forces”.
Phys. Rev. 73, 360. (1948).
Cruz y Cruz S., Rosas-Ortiz O. “Estados coherentes y gatos de Schroedinger”, Cinvestav 27, 30.
(enero-marzo 2008).
Lamoreaux S.K. “Demonstration of the Casimir Force in the 0.6 to 6 micro m Range”. Phys. Rev.
Lett. 78, 5. (1997).
Lifshitz E. “The theory of molecular attractive forces between solids”. Sov. Phys. JETP 2, 73. (1956).
Lifshitz E., Dzyaloshinskii I.E. and Pitaevskii L.P. “The general theory of van der Waals forces”.
Adv. Phys. 10, 165. (1961).
Munday J.N., Capasso F. and Parsegian V.A. “Measured long-range repulsive Casimir-Lifshitz forces”, Nature 457, Num. 7226, 170. (2009)
Rosas-Ortiz O. “Detrás de la magnetorresistencia gigante”, Conversus, Num. 66, 12 (dic 2007-ene
2008)
Torres G. “La transición entre lo macroscópico y lo atómico”, Conversus, Num. 72, 12. (2008)
Nota
“This force may be interpreted as a zero point pressure of electromagnetic waves. Although the
effect is small, an experimental confirmation seems not unfeasable and might be of certain interest”. El texto es tomado de Casimir (1948).
1
IPN
Donde la ciencia se convierte en cultura
23