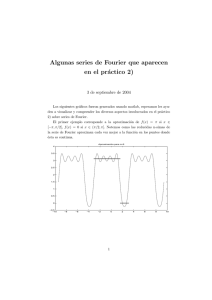
Sergio Fuentes Navarro PFC
Anuncio

Proyecto Fin de Carrera Ingeniería Aeronáutica Resolución de ecuaciones en derivadas parciales mediante métodos numéricos. Aplicación a problemas de control. Autor: Sergio Fuentes Navarro Tutor: José Ángel Acosta Rodríguez Equation Chapter 1 Section 1 Dep. de Ingeniería de Sistemas y Automática Escuela Técnica Superior de Ingeniería Universidad de Sevilla Sevilla, 2015 Proyecto Fin de Carrera Ingeniería Aeronáutica Resolución de ecuaciones en derivadas parciales mediante métodos numéricos. Aplicación a problemas de control. Autor: Sergio Fuentes Navarro Tutor: José Ángel Acosta Rodríguez Profesor titular Dep. de Ingeniería de Sistemas y Automática Escuela Técnica Superior de Ingeniería Universidad de Sevilla Sevilla, 2015 Proyecto Fin de Carrera: Resolución de ecuaciones en derivadas parciales mediante métodos numéricos. Aplicación a problemas de control. Autor: Sergio Fuentes Navarro Tutor: José Ángel Acosta Rodríguez El tribunal nombrado para juzgar el Proyecto arriba indicado, compuesto por los siguientes miembros: Presidente: Vocales: Secretario: Acuerdan otorgarle la calificación de: Sevilla, 2015 El Secretario del Tribunal Agradecimientos A mi familia, por no dejar de apoyarme en ningún momento. A mi tutor, José Ángel. 1 Resumen El presente trabajo tiene como objeto el estudio del uso de dos métodos numéricos (método de los residuos ponderados y método de los elementos finitos) para la aproximación de ecuaciones en derivadas parciales y su posterior aplicación a un problema de control automático: el péndulo invertido. Se presentará una explicación general de ambos métodos con varios ejemplos sacados de diferentes campos de la ingeniería y se presentarán los resultados obtenidos de la aplicación al problema de control. El lenguaje de programación en el que se ha escrito el código es MATLAB, habiendo hecho uso del Symbolic Math Toolbox (toolbox de cálculo simbólico). En el Anexo se encuentran los códigos comentados. Al final del trabajo se recogen las conclusiones obtenidas y posibles líneas de trabajo a seguir. Índice general I Introducción 5 1. Presentación del problema 1.1. Motivación y objetivos . . . . . . . . . . . . . . . . . . . . . . . . 1.2. Introducción a la resolución de ecuaciones diferenciales . . . . . . 1.2.1. Notación . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 6 6 7 II 8 Métodos numéricos 2. Método de los residuos ponderados 10 2.1. Desarrollo teórico . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 2.1.1. Aproximación de funciones mediante residuos ponderados 10 2.1.2. Selección de los pesos . . . . . . . . . . . . . . . . . . . . 12 2.1.3. Aproximación a la solución de ecuaciones diferenciales . . 14 2.1.3.1. Condiciones de borde satisfechas por las funciones de prueba . . . . . . . . . . . . . . . . . . . 14 2.1.3.2. Condiciones de borde no satisfechas por las funciones de prueba . . . . . . . . . . . . . . . . . . 14 2.1.4. Consideraciones sobre la convergencia . . . . . . . . . . . 15 2.2. Ejemplos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 2.2.1. Aproximación de una función de una variable . . . . . . . 16 2.2.2. Aproximación de ecuaciones diferenciales . . . . . . . . . 18 2.2.2.1. Caso unidimensional: se satisfacen las condiciones de borde . . . . . . . . . . . . . . . . . . . . 18 2.2.2.2. Caso bidimensional: Problema de torsión . . . . 20 2.2.2.3. Variación del problema de torsión. No se satisfacen las condiciones de borde . . . . . . . . . . 21 2.3. Comentarios finales sobre el MRP . . . . . . . . . . . . . . . . . 22 3. Método de los elementos finitos 3.1. Teoremas para el cálculo de integrales y derivadas . . 3.2. Desarrollo teórico del Método de los elementos finitos 3.2.1. Tipos de elemento . . . . . . . . . . . . . . . . 3.2.1.1. Elemento unidimensional . . . . . . . 2 . . . . . . . . . . . . . . . . . . . . . . . . 23 23 25 27 27 3 ÍNDICE GENERAL 3.2.1.2. Elementos bidimensionales . . . . . . . . . . . . 3.2.2. Condiciones sobre las funciones de pequeño soporte . . . . 3.2.3. Elementos isoparamétricos . . . . . . . . . . . . . . . . . . 3.2.3.1. Unidimensionales . . . . . . . . . . . . . . . . . 3.2.3.2. Bidimensionales . . . . . . . . . . . . . . . . . . 3.3. Ejemplos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.3.1. Planteamiento de un problema unidimensional. Formulación débil. . . . . . . . . . . . . . . . . . . . . . . . . . . . 3.3.2. Ejemplos de cálculo de matriz de rigidez . . . . . . . . . . 3.4. Propiedades de K y F . . . . . . . . . . . . . . . . . . . . . . . . 4. Sistema péndulo invertido 4.1. Descripción del sistema mecánico . . . . . . . 4.2. Descripción del controlador . . . . . . . . . . 4.3. Planteamiento de la resolución de la ecuación ciales asociada al sistema péndulo . . . . . . . 4.3.1. Condiciones de contorno aproximadas . . . . . . . . . . . . . . . . . . . . . . en derivadas par. . . . . . . . . . . . . . . . . . . . . . 5. Método de los residuos ponderados 5.1. Galerkin . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.1.1. Consideraciones previas . . . . . . . . . . . . . . 5.1.1.1. Necesidad de un dominio no simétrico . 5.1.1.2. Segundo Orden . . . . . . . . . . . . . . 5.1.1.3. Traslación del problema . . . . . . . . . 5.1.2. Solución con Galerkin . . . . . . . . . . . . . . . 5.1.2.1. Aproximación mediante polinomios . . 5.1.2.2. Aproximación sinusoidal . . . . . . . . . 5.1.2.3. Condiciones de contorno originales . . . 5.1.3. Comentarios finales sobre el método de Galerkin 5.2. Dirac . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.2.1. Dirac en el dominio y Galerkin en el contorno . . 5.2.2. Comentarios finales sobre el método de Dirac . . 5.3. Resumen de resultados y conclusiones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 31 31 32 33 35 35 37 39 41 41 43 44 45 47 47 47 48 51 53 53 54 56 58 63 64 64 72 72 6. Método de los elementos finitos 74 6.1. Primer Orden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74 6.1.1. Planteamiento del residuo y mallado . . . . . . . . . . . . 74 6.1.2. Matrices elementales. Elementos isoparamétricos . . . . . 75 6.1.3. Condiciones de contorno . . . . . . . . . . . . . . . . . . . 77 6.1.4. Resultados . . . . . . . . . . . . . . . . . . . . . . . . . . 79 6.2. Segundo Orden . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 6.2.1. Resultados . . . . . . . . . . . . . . . . . . . . . . . . . . 80 6.3. Problemática asociada a la resolución mediante elementos rectangulares . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81 6.4. Conclusiones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84 ÍNDICE GENERAL 4 7. Trabajo futuro 85 8. Anexo 8.1. Código para residuos ponderados 8.1.1. Galerkin . . . . . . . . . . 8.1.2. Dirac . . . . . . . . . . . 8.2. Código para elementos finitos . . 8.2.1. Segundo orden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87 87 87 91 92 92 Parte I Introducción 5 Capítulo 1 Presentación del problema 1.1. Motivación y objetivos El objetivo de este proyecto de fin de carrera es continuar con la línea de trabajo realizada en [1] y [2]. Ambos proyectos estudiaban la resolución de una ecuación en derivadas parciales usando métodos numéricos: el método de las diferencias finitas en [1] y el método de los elementos finitos mediante Freefem (lenguaje de programación y software desarrollado para la resolución de ecuaciones en derivadas parciales usando el método de elementos finitos) así como una variación del método de las diferencias finitas en [2]. Este proyecto busca resolver el mismo problema a través de caminos distintos. El método de los residuos ponderados no usa malla alguna sobre el dominio, a diferencia de los anteriores. En base a los resultados obtenidos de este método se analizan las soluciones provenientes del método de los elementos finitos. 1.2. Introducción a la resolución de ecuaciones diferenciales A la hora de hacer un estudio cuantitativo de un fenómeno físico es necesario plantear un sistema de ecuaciones diferenciales (ordinarias o en derivadas parciales) sobre una cierta región del espacio y sujeto a las correspondientes condiciones iniciales y/o de borde. El siguiente paso es encontrar la solución de dichas ecuaciones. No obstante, en la mayoría de los casos esto no es trivial. Debido a la complejidad de la geometría o la distribución de cargas, no siempre es posible encontrar soluciones analíticas de forma sencilla: sólo las ecuaciones más simples pueden ser resueltas de forma exacta. Para solventar esta dificultad se procede a aproximar de forma numérica la ecuación: mediante una discretización del dominio se convierte un problema de infinitos grados de libertad en un problema algebraico que involucre un cierto número finito de parámetros. En este texto se presentará el método de los re6 CAPÍTULO 1. PRESENTACIÓN DEL PROBLEMA 7 siduos ponderados y el método de los elementos finitos con el fin de, siguiendo la estrategia recién expuesta, aproximar de forma numérica una ecuación en derivadas parciales. 1.2.1. Notación A continuación, vamos a introducir la notación utilizada a lo largo de este texto en lo que se refiere a ecuaciones diferenciales. Consideremos una ecuación diferencial, sobre un dominio Ω de contorno Γ , escrita como: A(u) = L(u) + p = 0 en Ω (1.1) donde L es un operador diferencial lineal actuando sobre la función a determinar u y p es independiente de u. Como ilustración de esta notación ponemos el caso de la ecuación de Poisson, de aplicación, por ejemplo, a la hora de calcular el potencial electrostático dada una densidad de carga: ∇2 V = − ρ ε0 (1.2) siendo V el potencial, ρ la densidad de carga y ε0 la permitividad del vacío. Entonces, en coordenadas cartesianas: L(V ) = ∂ 2 V (x, y) ∂ 2 V (x, y) + ∂x2 ∂y 2 (1.3) ρ ε0 (1.4) p(x, y) = Las condiciones de contorno se expresan de forma similar: B(u) = M(u) + r = 0 en Γ (1.5) con M(u) un operador lineal adecuado y r independiente de u. Por ejemplo, las condiciones de borde de Dirichlet y Neumann (valor de la función y de la derivada de la función en la frontera, respectivamente) para una ecuación diferencial quedan: M(u) = u M(u) = −k ∂u ∂n r = −ū r = −σ̄ en Γu en Γσ (1.6) (1.7) Parte II Métodos numéricos 8 9 En esta segunda parte se presentan los dos métodos numéricos que se aplicarán al problema de estudio, ya adelantados en la introducción: el método de los residuos ponderados y el método de los elementos finitos. Dividiremos los capítulos correspondientes a la explicación de estos métodos en una primera parte teórica y una segunda parte con varios ejemplos. Capítulo 2 Método de los residuos ponderados El método de los residuos ponderados (MRP) es un método de aproximación que propone una solución compuesta por la suma del producto de una serie de funciones, llamadas funciones de prueba, por unos coeficientes a determinar (nuevas incógnitas). A través de una formulación integral que tiene como objetivo la minimización del error medio se hallan los valores de dichos coeficientes y con ello se construye la aproximación. 2.1. Desarrollo teórico Este apartado teórico presenta el MRP aplicado a la aproximación de funciones y de ecuaciones diferenciales, un apartado dedicado a la selección de ciertas funciones (relevantes a la hora de la aplicación del MRP) así como algunos comentarios sobre convergencia. 2.1.1. Aproximación de funciones mediante residuos ponderados Vamos a introducirnos en el estudio del MRP a través de una de sus posibles aplicaciones, la aproximación de funciones. El objetivo será aproximar la función φ en el dominio Ω. Partiremos de una aproximación del tipo: φ ≈ φ̂ = ψ + M X Nm am (2.1) m=1 siendo ψ la función que verifica las condiciones de borde (en todos o en alguno 10 CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS 11 de los bordes), Nm las funciones de prueba y am las nuevas incógnitas, esto es, los parámetros a determinar para generar la aproximación. En los bordes donde la función ψ ajuste la solución, las funciones de prueba habrán de ser nulas. Estas funciones tienen que ser continuas en el dominio de integración. Como ya se ha adelantado, se busca que el residuo medio ponderado en el dominio de integración sea nulo. Comenzamos, pues, definiendo el residuo como: RΩ = φ − φ̂ en Ω (2.2) siendo φ la solución exacta (función que se pretende determinar) y φ̂ su aproximación. Se pretende que este error, ponderado con una serie de funciones (que más adelante se abordarán en mayor detalle) e integrado en todo el dominio, sea nulo. De forma análoga, en las fronteras donde no queden satisfechas las condiciones de borde existirá, además, un residuo RΓ , aunque de momento, por comodidad, supondremos que se verifican todas las condiciones de borde y este error es nulo. Expresando lo anterior de forma matemática: ˆ Wl RΩ dΩ = 0 l = 0, 1, 2, .., M (2.3) Ω Introduciendo (2.1) en (2.3) se llega a un sistema algebraico de M ecuaciones y M incógnitas del que se hallan los coeficientes que hacen el residuo medio nulo (la solución será exacta en los bordes donde ψ aproxime la función; en general, en el interior, el error será distinto de cero). Desarrollando (2.3) conocida la aproximación (2.1): ˆ ˆ Ω ˆ Wl (φ − φ̂)dΩ = Wl RΩ dΩ = Ω Wl (φ − ψ − ˆ Wl (φ − ψ)dΩ − Ω Nm am )dΩ = (2.4) m=1 Ω ˆ M X Wl Ω M X Nm a m = 0 m=1 De las propiedades de las integrales sabemos que la integral de una suma es igual a la suma de las integrales, luego: ˆ ˆ X Wl (φ − ψ)dΩ − am Wl Nm dΩ = 0 (2.5) Ω Ω lo que puede escribirse como: Ka = f Siendo K la matriz de coeficientes del sistema, cuyos elementos son: ˆ Klm = Wl Nm dΩ, Ω (2.6) (2.7) CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS f el vector de términos independientes, de componentes: ˆ fl = Wl (φ − ψ)dΩ 12 (2.8) Ω y a el vector de incógnitas a = [a1 , a2 , ..., aM ]. 2.1.2. Selección de los pesos Las variaciones sobre el MRP se basan principalmente en la elección de las funciones con los que se pondera el error (de aquí en adelante se usará pesos para referirse a ellas). Las técnicas más comunes son colocación por puntos, colocación por subdominios, mínimos cuadrados y Galerkin (véase [5, capítulo 1] ). Se describen sucintamente a continuación para el caso unidimensional (la idea es extensible a mayor dimensión). Colocación por puntos. Los pesos se definen mediante una delta de Dirac centrada en el punto elegido. Esto es: Wl = δ(x − xl ) (2.9) con δ(x − xl ) la función delta de Dirac, centrada en xl , que cumple las siguientes propiedades: ( δ(x − xl ) = 0 si x 6= xl (2.10) δ(x − xl ) = ∞ si x = xl ˆ f (x)δ(x − xl )dx = f (xl ) (2.11) x donde el índice l va recorriendo todos los puntos, xl , donde se han situado las deltas. Sustituyendo (2.9) en (2.7) y (2.8) se obtiene: Klm = Nm |x=xl (2.12) fl = (φ − ψ) |x=xl (2.13) Colocación por subdominios. Las funciones de peso se definen como sigue: ( 1 si xl < x < xl+1 Wl = (2.14) 0 si x < xl o x > xl+1 En este caso, xl y xl+1 representan las coordenadas de los extremos del subdominio l-ésimo. Con un desarrollo similar se llega a: CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS 13 ˆ Nm dx (2.15) (φ − ψ)dx (2.16) Klm = x ˆ fl = x Mínimos cuadrados. Se trata de minimizar el cuadrado del residuo (distancia entre solución y aproximación) en cada punto. Se pretende minimizar: ˆ F (a1 , ..., aM ) = (φ − φ̂)2 dΩ (2.17) Ω Para minimizar, se iguala la derivada parcial de la función F (a1 , ..., aM ) con respecto a cada uno de los parámetros a cero: ∂F =0 ∂al para l = 1, 2, ..., M (2.18) Teniendo en cuenta (2.1) se obtiene: ∂F = Nl ∂al Entonces, F es mínimo cuando: ˆ (φ − φ̂)Nl dΩ (2.19) (2.20) Ω expresión que comparada con (2.3) lleva a que ambas sean iguales si Nl = Wl obteniéndose en este caso las siguientes expresiones para la matriz K y el vector f: ˆ Klm = Nl Nm dΩ (2.21) ˆ Ω Nl (φ − ψ)dΩ fl = (2.22) Ω Galerkin. Las funciones de peso son las mismas que las funciones de prueba, es decir, Nl = Wl . Si se introduce esto en las ecuaciones (2.7) y (2.8) se tiene: ˆ Klm = Nl Nm dΩ (2.23) Ω CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS 14 ˆ (2.24) Nl (φ − ψ)dΩ fl = Ω Expresiones que coinciden con las del caso de mínimos cuadrados. La matriz K resultante es simétrica, lo que supone una gran ventaja en términos computacionales. 2.1.3. Aproximación a la solución de ecuaciones diferenciales Se hará aquí una distinción de casos, según las condiciones de borde sean o no satisfechas por las funciones de prueba. 2.1.3.1. Condiciones de borde satisfechas por las funciones de prueba Partimos P de (1.1). Si se propone una aproximación de u, dada por u ≈ û = ψ + Nm am con la función ψ aproximando las condiciones de borde y Nm aproximando la solución en el dominio, y se introduce en (1.1) se ve que, en general, el segundo miembro de la igualdad será distinto de cero por estar usando una aproximación: este es el error que se comete. Ponderando con los pesos correspondientes e integrando en el dominio: ˆ ˆ ˆ Wl RΩ dΩ = Wl A(û)dΩ = Wl (L(û) + p)dΩ = (2.25) Ω Ω ˆ Wl [L(ψ + Ω ˆ M X am Nm )]dΩ + Wl pdΩ = 0 m=1 Ω Reagrupando, se obtiene: ˆ Klm = Wl L(Nm )dΩ 1≤l≤M Ω Ω ˆ fl = 1≤m≤M (2.26) ˆ Wl L(ψ)dΩ Wl pdΩ + Ω y 1≤l≤M (2.27) Ω expresiones que llevan al problema algebraico Ka + f = 0 . 2.1.3.2. Condiciones de borde no satisfechas por las funciones de prueba Que las condiciones de borde no queden P satisfechas se traduce en ψ = 0. La aproximación propuesta pasa a ser u ≈ û = Nm am . Hay que tener en cuenta que, en este caso, aparecerá, además del error en el dominio al aproximar A(u) 15 CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS por A(û) un error en el borde igual a B(û). Matemáticamente seguimos un proceso análogo al anterior, la ponderación e integración del residuo: ˆ ˆ Wl RΩ dΩ + Ŵl RΓ dΓ = 0 (2.28) Ω Γ donde las Ŵl son los pesos utilizados al ponderar el residuo en el contorno. Estos pesos pueden elegirse distintos a los pesos usados para la ponderación en el dominio. Con un desarrollo similar al anterior: ˆ ˆ Wl L(Nm )dΩ + Klm = Ω Ŵl M(Nm )dΓ 1≤l≤M y Γ ˆ fl = (2.29) ˆ Wl pdΩ + Ω Ŵl rdΓ 1≤l≤M (2.30) Γ Ka + f = 0 2.1.4. 1≤m≤M (2.31) Consideraciones sobre la convergencia Antes de pasar a los ejemplos, cabe preguntarse cómo puede conocerse cuándo la solución aportada por el MRP es lo suficientemente precisa. La convergencia es algo que debe estudiarse siempre que se utilicen técnicas de aproximación: rara vez conoceremos la solución exacta de una ecuación, de donde nace la necesidad de un criterio para determinar la exactitud. Para el estudio de la convergencia del MRP, en general, se van obteniendo sucesivas soluciones, cada una de ellas con un parámetro más que la anterior, hasta que se ve que la solución obtenida apenas difiere al aumentar el número de parámetros en las aproximaciones propuestas. El método ha convergido, pero ¿ha convergido a la solución real? En este texto se asumirá que la convergencia es a la solución real del problema. En el caso de algunos problemas físicos puede hacerse un análisis de conservación de masa, conservación de energía, equilibrio o estabilidad entre otros para determinar la factibilidad de la solución. 2.2. Ejemplos Utilizando los resultados teóricos obtenidos en la sección anterior vamos a analizar algunos ejemplos del uso del MRP para la aproximación tanto de funciones como de ecuaciones diferenciales. CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS 2.2.1. 16 Aproximación de una función de una variable Empleando el MRP vamos a encontrar una aproximación a una cierta función y mostrar las diferencias halladas en el resultado cuando se utiliza cada uno de los tipos de funciones de peso anteriormente descritos. La función a aproximar es: x )sen(1,7πx) x ∈ [0, 1] 3 Se propone una aproximación con una función que satisfaga las condiciones de borde y dos funciones de prueba que aproximen en el dominio: φ(x) = −(0,1 + φ̂ = ψ + a1 N1 + a2 N2 ψ = 0,350574030895811x N1 = x(1 − x) N2 = x2 (1 − x) Se comprueba que las Nm son nulas en los extremos del intervalo y ψ cumple las condiciones de borde. Colocación por puntos. Con dos puntos: x1 = 0,25 y x2 = 0,75. K11 = N1 (x1 ) = 0,1875 K12 = N2 (x1 ) = 0,046875 K21 = N1 (x2 ) = 0,1875 K22 = N2 (x2 ) = 0,140625 f1 = φ(x1 ) − ψ(x1 ) = −0,2659113 f2 = φ(x2 ) − ψ(x2 ) = −0,0032116 Despejando: a1 −2,1358546 = a2 −2,87064426 Colocación por subdominios. Dos subdominios: el primero entre el origen y el punto medio del segmento; el otro, de punto medio a final. Entonces, x1 = 0, x2 = 0,5 y x3 = 1. K11 = 0,5 ´ N1 (x)dx = 0,083333 K12 = 0 K21 = ´1 0,5 0,5 ´ N2 (x)dx = 0,0260416 0 N1 (x)dx = 0,0833333 K22 = ´1 0,5 N2 (x)dx = 0,0572916 CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS f1 = 17 0,5 ´ [φ(x) − ψ(x)]dx = −0,11234019 0 f2 = ´1 0,5 [φ(x) − ψ(x)]dx = −0,02452481 Dando como parámetros: a1 −2,226236221 = a2 −2,8100923155 Mínimos cuadrados. Las expresiones coinciden con las de Galerkin ((2.23) y (2.24)). K11 = ´1 N1 (x)N1 (x)dx = 1/30 K12 = 0. K21 = ´1 ´1 N1 (x)N2 (x)dx = 1/60 0. N2 (x)N1 (x)dx = 1/60 K22 = 0. f1 = ´1 ´1 N2 (x)N2 (x)dx = 1/105 0. N1 (x)[φ(x) − ψ(x)]dx = −0,03053668742 0 f2 = ´1 N2 (x)[φ(x) − ψ(x)]dx = −0,01192414968 0 Resolviendo a1 a2 = −2,32066211519 −2,80912298519 La Figura 2.1 muestra la función original y las gráficas de las distintas aproximaciones. Figura 2.1: Aproximación de una función mediante MRP. CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS 2.2.2. 18 Aproximación de ecuaciones diferenciales Presentamos 3 casos: un problema unidimensional, uno bidimensional y una variación de este para ejemplificar el uso del MRP tanto si se satisfacen las condiciones de borde como si no. 2.2.2.1. Caso unidimensional: se satisfacen las condiciones de borde Nos disponemos a usar el MRP para resolver la ecuación: ∂2u −u=0 ∂x2 con las condiciones: ( u = 0 en x = 0 u = 1 en x = 1 en el intervalo x ∈ [0, 1] . Esas condiciones pueden reescribirse como: ( M(u) = u en x = 0 M(u) = u en x = 1 ( r=0 en x = 0 r = −1 en x = 1 La solución exacta de la ecuación es una combinación lineal de senos y cosenos hiperbólicos: u(x) = Acosh(x) + Bsenh(x) u(0) = A = 0 u(1) = Bsenh(1) = 1 → B = 1 senh(1) Por tanto: u(x) = senh(x)/senh(1) Para la función ψ adoptamos: ψ=x y las funciones de aproximación Nm serán de tipo sinusoidal: Nm (x) = sen(mπx) En este problema: m = 1, 2, ..., M CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS L() = 19 ∂ 2 () − () ∂x2 p=0 Tomaremos M=2 y como funciones de peso el método de colocación (con x1 = 1/3 y x2 = 2/3) y de Galerkin de cara a una comparación. Colocación. K11 = (1 + π 2 )sen(π/3) K12 = (1 + 4π 2 )sen(2π/3) K21 = (1 + π 2 )sen(2π/3) K22 = (1 + 4π 2 )sen(4π/3) f1 = −1/3 a1 a2 f2 = −2/3 = −0,05312 0,004754 Galerkin K11 = 0,5(1 + π 2 ) K22 = 0,5(1 + 4π 2 ) K21 = 0 f1 = −1/π a1 a2 K12 = 0 f2 = 1/2π = −0,05857 0,007864 La Figura 2.2 muestra la función original y las gráficas de las distintas aproximaciones. CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS 20 Figura 2.2: Comparación Galerkin-Colocación por puntos. 2.2.2.2. Caso bidimensional: Problema de torsión Este ejemplo está sacado de [5, capítulo 1]. El problema de torsión (bidimensional) queda definido por la ecuación: ∇2 Ψ = ∂ 2 Ψ(x, y) ∂ 2 Ψ(x, y) + = −2αG ∂x2 ∂y 2 Ψ = 0 en Γ φ es la función de tensión, α el giro por unidad de longitud y G el módulo de elasticidad trasversal. Hallada la función de tensión pueden obtenerse, primero, los esfuerzos, y por integración, el momento torsor T : ˆ T = 2 Ψ(x, y)dxdy Tomaremos por simplicidad αG = 1 y un dominio rectangular −3 ≤ x ≤ 3 , −2 ≤ y ≤ 2. Las funciones de prueba elegidas son: φ1 (x, y) = cos(πx/6)cos(πy/4) φ2 (x, y) = cos(πx/2)cos(πy/4) φ3 (x, y) = cos(πx/6)cos(3πy/4) funciones que cumplen las condiciones de borde. Para este problema, el operador diferencial L y la función p son: L() = ∂ 2 () ∂ 2 () + ∂x2 ∂y 2 p=2 CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS 21 con lo que, si usamos el método de Galerkin: ˆ3 ˆ2 Klm = − φl ( ∂ 2 φm ∂ 2 φm + )dydx 2 ∂x ∂y 2 −3 −2 ˆ3 ˆ2 fl = 2φl dydx −3 −2 Debido a la ortogonalidad de las funciones de prueba, el sistema de ecuaciones resulta diagonal y la solución es inmediata: a1 4608/13π 4 a2 = −4608/135π 4 −4608/255π 4 a3 2.2.2.3. Variación del problema de torsión. No se satisfacen las condiciones de borde Resolvemos el mismo problema de torsión del apartado anterior pero ahora las funciones de prueba elegidas no cumplirán las condiciones de borde y serán, para una aproximación con 5 términos: φ1 = 4 − y 2 φ2 = x 2 φ1 φ3 = y 2 φ1 φ3 = y 2 x 2 φ1 φ5 = x 4 φ1 Volviendo a plantear el residuo y teniendo en cuenta el error que se produce en el borde: ˆ3 ˆ2 ∂ 2 Ψm ∂ 2 Ψm + )dydx + ( ∂x2 ∂y 2 −3 −2 llegando al sistema: ˆ2 h −2 ˆ2 h i W̄l Ψ̂ |x=3 dy − W̄l Ψ̂ |x=−3 dy = 0 i −2 22 CAPÍTULO 2. MÉTODO DE LOS RESIDUOS PONDERADOS 6,7 −12 11,7 9,6 −237,6 −44 −333,6 −16 −163,2 −3156,7 43,7 80 105,6 355,2 159,1 389,5 433,4 1971,6 432 1473,7 2.3. a1 a2 a3 a4 a5 = 813,6 −5748,7 −547,2 −3932,4 −46239,4 1,1713 −0,1440 −0,0889 0,0254 −0,0004 a1 a2 a3 a4 a5 = 12 36 16 48 194,4 Comentarios finales sobre el MRP Las funciones de prueba utilizadas en los ejemplos anteriores son de carácter global, esto es, se aplican sobre todo el dominio y han de satisfacer ciertas condiciones en el contorno: la calidad de la solución obtenida está en directa relación con la elección de estas funciones. Por tanto, dicha elección se torna elemento clave en el problema y como cabría esperar la dificultad crece con la dimensión del problema. Un conjunto de funciones de prueba inapropiado podría dar lugar a una matriz K mal condicionada, dificultando o imposibilitando la resolución del sistema. Si algo se le puede reprochar al MRP es precisamente eso, el no aportar una metodología sistemática para la determinación de las funciones de aproximación. Capítulo 3 Método de los elementos finitos Antes de comenzar con la teoría del método de elementos finitos, vamos a ocuparnos en la siguiente sección de enunciar una serie de elementos teóricos que serán de utilidad en los cálculos que se lleven a cabo en este capítulo. 3.1. Teoremas para el cálculo de integrales y derivadas A continuación se recuerdan varios resultados (extraídos de [5, capítulos 1 y 2]) que serán de interés para los cálculos venideros: Teorema de Green. Sea una función u y el operador diferencial dv, definidas en un dominio bidimensional Ω cuyo contorno es Γ, entonces: ˆ ˆ ˆ ∂v ∂u u dxdy = uvnx dΓ − v dxdy (3.1) ∂x ∂x Ω ˆ u Γ ∂v dxdy = ∂y Ω Ω ˆ ˆ uvny dΓ − Γ v ∂u dxdy ∂y (3.2) Ω siendo nx , ny los cosenos directores de la normal saliente n al contorno cerrado Γ que rodea a Ω. La integración se realiza en sentido antihorario. Cambio de variables. Sea una función real integrable f definida en el intervalo [x1 , x2 ] (f : [x1 , x2 ] → R) y sea x una función continuamente diferenciable que cumple x(ξ1 ) = x1 y x(ξ2 ) = x2 , entonces: ˆx2 ˆξ2 f (x)dx = x1 f (x(ξ)) ξ1 23 ∂x(ξ) dξ ∂ξ CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 24 se denomina Jacobiano de la transformación. Puede El término ∂x(ξ) ∂ξ reescribirse, entonces: ˆξ2 ˆx2 f (x)dx = x1 f (x(ξ))|J|dξ ξ1 Regla de la cadena. Sea una función f integrable y diferenciable (f : [x1 , x2 ] → R) y x una función continuamente diferenciable (x : [ξ1 , ξ2 ] → [x1 , x2 ]). Entonces: ∂[f (x(ξ))] ∂x(ξ) ∂ [f (x(ξ))] = ∂ξ ∂x ∂ξ (3.3) Cuadratura de Gauss. La cuadratura de Gauss aproxima el valor de una integral por un sumatorio de los valores de la función ponderados por unos ciertos coeficientes en un número finito de puntos: ˆx2 f (x)dx = N X f (xi )Wi i=1 x1 donde los coeficientes Wi se pueden interpretar como el ancho del rectángulo cuya altura es f (xi ). Nos centramos aquí en la cuadratura de Gauss-Legendre, de interés a la hora de aproximar funciones polinómicas, con una normalización del dominio tal que la variable independiente va desde −1 a 1. Usando n puntos esta cuadratura permite conocer el valor exacto de una integral siempre que la función polinómica sea de orden 2n − 1. Si la función no cumple esta condición o no es polinómica se obtiene una aproximación. Esta regla de cuadratura puede ser extendida a más dimensiones: suponiendo un dominio bidimensional, tenemos: ˆ1 ˆ1 f (ξ, η)dξdη = N2 N1 X X g(ξi , ηj )Wi W̄j i=1 j=1 −1 −1 Sin profundizar matemáticamente, nos limitaremos a usar aquí los puntos y pesos que se obtienen de una cuadratura con 2 puntos, siendo estos puntos P = ± √13 y los pesos asociados, ambos, W = 1 (véase [4, capítulo 6]). Como ejemplo, se desea calcular el valor de la integral: ˆ1 ˆ1 9ξ 2 η 2 dξdη −1 −1 El número de puntos de integración será: 2 = 2n − 1 → n = 1,5 CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 25 al tener que tomar un número entero de puntos, se usarán 2 puntos para ambas variables. Los puntos de integración y pesos son: 1 ξ1 = η1 = − √ 3 1 ξ2 = η2 = √ 3 W1 = W̄1 = 1 W2 = W̄2 = 1 El resultado de la cuadratura coincide con el de la integral, siendo el valor de esta 4. 3.2. Desarrollo teórico del Método de los elementos finitos En contrapartida a la visión global del MRP, se presenta en esta sección el Método de los elementos finitos (MEF). La idea de este método es parecida a la del MRP, es decir, transformar una ecuación diferencial en un sistema algebraico proponiendo una aproximación para la solución en función de una serie de parámetros (las nuevas incógnitas) y llegando a un sistema de ecuaciones lineales: Ka = f (3.4) del que despejar el vector a y poder reconstruir la aproximación y donde K y f tienen el mismo significado que en el MRP: matriz de coeficientes del sistema y vector de términos independientes, provenientes de una integración del residuo, ponderado por unos ciertos pesos, en la región de estudio. Se suele denominar matriz de rigidez a la matriz K y vector de fuerzas al vector f. La interpretación de los elementos K y f depende del contexto del problema que se está tratando. Por ejemplo, si se está llevando a cabo un cálculo estructural, el elemento (i, j) de K relaciona los desplazamientos del nodo j con las fuerzas aplicadas en el nodo i , esto es, la componente i del vector de fuerzas; si se trata de un problema de transferencia de calor, el elemento (i, j) representa la relación entre la temperatura del nodo j y el flujo de calor en el nodo i (componente j del vector f ), etc. En general, las fórmulas para el cálculo de K y f vendrán dadas por integrales cuyo integrando dependerá del problema que se esté tratando. En la sección 3.3 se ejemplifica el desarrollo matemático necesario para llegar, a partir de la ecuación diferencial que se pretenda resolver, a las expresiones particulares de la matriz de rigidez y del vector de fuerzas. Al final de la sección 2.3 ya quedaron indicados los problemas de condicionamiento de la matriz K debidos a que las funciones de aproximación debían CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 26 Figura 3.1: Dominio Ω al aplicar el MEF. cumplir una serie de condiciones en los bordes. El MEF propone como alternativa la división del dominio en regiones más pequeñas y la reconstrucción por tramos de la solución. El dominio, esquematizado en la Figura 3.1 , pasa a estar dividido en una serie de regiones o subdominios, llamados a partir de aquí elementos, no superpuestos, de forma que: Ω= NE X Ωe i=1 Γ= NE X Γe i=1 De esta forma, (2.28) puede reescribirse como: ˆ ˆ Wl RΩ dΩ + Ω Ŵl RΓ dΓ = Γ NE ˆ X i=1 Ωe e Wle RΩ dΩe + NE ˆ X Wˆle RΓe dΓ = 0 i=1 Γe donde las variables con superíndice e hacen referencia al dominio elemental y N E es el número de elementos en los que se ha dividido el dominio. Pueden emplearse distintos tipos de elemento dentro del mismo dominio y distintas funciones en cada elemento. La aproximación de φ̂ es por tramos, lo que puede CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 27 traer consigo algún tipo de discontinuidad en las funciones o sus derivadas, algo que habrá que tener en cuenta para la formulación del problema. Como funciones de aproximación se tomaran funciones de pequeño soporte o de soporte compacto, asociadas a cada nodo, que se definen como aquellas funciones que son nulas en todos los nodos excepto sobre el que se han definido. Pueden expresarse como: − Hi (→ rj ) = δij (3.5) siendo δij la delta de Kronecker: ( δij = 1 si i = j 0 si i 6= j − y donde el vector → rj = (xj,1 , xj,2 , ..., xj,n ) representa las variables de que depende el problema. Estas Hi serán calculadas en el apartado siguiente para − el caso de elementos unidimensionales y bidimensionales, donde → rj = (xj ) y → − rj = (xj , yj ) respectivamente. Pueden extenderse, por supuesto, al caso tridimensional siguiendo el mismo principio. La aproximación que se lleva a cabo es la siguiente: u≈ n X u i Hi (3.6) i=1 siendo ui el valor de la función en cada uno de los n nodos y Hi la función de pequeño soporte correspondiente al nodo i-ésimo. 3.2.1. Tipos de elemento Se presentan aquí los elementos más usados al tratar problemas a través de la metodología los elementos finitos para problemas unidimensionales y bidimensionales y se calculan las funciones de pequeño soporte correspondientes a cada caso. 3.2.1.1. Elemento unidimensional Sea un dominio unidimensional, como el que se ve en la Figura 3.2, con 2 nodos. Se define en cada nodo una función lineal en x: CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 28 Figura 3.2: Dominio unidimensional. H1 = xi+1 − x hi H2 = x − xi hi donde hi = xi+1 − xi , esto es, la longitud del elemento. Se ve que que cumple lo expresado por la ecuación (3.5), esto es: H1 (xi ) = 1 H1 (xi+1 ) = 0 H2 (xi ) = 0 H2 (xi+1 ) = 1 Al tenerse dos nodos, puede proponerse por tanto una aproximación lineal en cada elemento. Particularizando (3.6): u = u1 H1 (x) + u2 H2 (x) Se podrían calcular las funciones de pequeño soporte para un elemento unidimensional con, por ejemplo, tres nodos, sin más que proponer Hi parabólicas y obtener el valor de las constantes a partir de la condición (3.5). 3.2.1.2. Elementos bidimensionales En este apartado se llega a las expresiones generales de las funciones de forma para elementos triangulares y cuadriláteros. Elementos triangulares CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 29 Elementos triangulares con 3 nodos, como el que se ve en la Figura 3.3 , permiten una aproximación mediante un polinomio de grado uno en x e y: u(x, y) = a1 + a2 x + a3 y o de otra manera: a1 y] a2 a3 u(x, y) = [1 x Figura 3.3: Elemento triangular. 3 Nodos. Si sustituimos para cada nodo llegamos u1 1 x1 u2 = 1 x2 u3 1 x3 a: y1 a1 y2 a2 y2 a3 y despejando los coeficientes: x2 y3 − x3 y2 a1 1 a2 = y2 − y3 2A x3 − x2 a3 x3 y1 − x1 y3 y3 − y1 x1 − x3 x1 y2 − x2 y1 u1 u2 , y1 − y2 x2 − x1 u3 donde: 1 1 A = det 1 2 1 x1 x2 x3 y1 y2 , y2 en el caso de que la numeración de los nodos se lleve a cabo en el sentido contrario al de las agujas del reloj y donde A representa el área del elemento triangular. En la programación del MEF, la numeración de los nodos debe seguir siempre el mismo sentido para cada elemento del dominio. De la ecuación (3.6) tenemos, en este caso, una aproximación del tipo: u = u1 H1 (x, y) + u2 H2 (x, y) + u3 H3 (x, y) CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 30 con: H1 (x, y) = 1 [(x2 y3 − x3 y2 ) + (y2 − y3 )x + (x3 − x2 )y] 2A (3.7) H2 (x, y) = 1 [(x3 y1 − x1 y3 ) + (y3 − y1 )x + (x1 − x3 )y] 2A (3.8) H3 (x, y) = 1 [(x1 y2 − x2 y1 ) + (y1 − y2 )x + (x2 − x1 )y] 2A (3.9) Elementos cuadriláteros Un elemento como el de la Figura 3.4, al tener cuatro nodos, permite una aproximación polinómica con cuatro términos: u(x, y) = a1 + a2 x + a3 y + a4 xy que conduce, con un procedimiento análogo al usado para el caso triangular, a unas funciones de forma: H1 (x, y) = 1 (b − x)(c − y) 4bc (3.10) H2 (x, y) = 1 (b + x)(c − y) 4bc (3.11) 1 (b + x)(c + y) 4bc 1 (b − x)(c + y) H4 (x, y) = 4bc (3.12) H3 (x, y) = Figura 3.4: Elemento rectangular. 4 Nodos. (3.13) CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 3.2.2. 31 Condiciones sobre las funciones de pequeño soporte Sean (1.1) y (1.5) las expresiones generales de una ecuación diferencial y de las condiciones de borde asociadas, que pueden, como se hizo al explicar el MRP, ponderarse, integrarse y sumarse para hallar el residuo ponderado. Viendo la estructura de la ecuación, en la que aparecen los operadores L y M, cabe preguntarse cuáles son las condiciones que deben cumplir las funciones de pequeño soporte para poder utilizarse en la formulación del problema por elementos finitos. Estas son 3 (véase [6]): Continuidad. En la interfaces entre elementos, las funciones de prueba y cualquiera de sus derivadas (hasta orden N-1, siendo N el orden de la derivada más alta que aparece en el residuo) deben ser continuas. Completitud. La solución aproximada ha de ser capaz de representar cualquier variación de la función incógnita en el dominio. Si la función de aproximación fuese un polinomio tipo ao + a1 x + ... + aN +1 xN , todos los coeficientes ao , a1 , ..., aN +1 deben ser distintos de cero. Isotropía espacial. La función de ser invariante a cambios en el sistema de coordenadas. Por ejemplo, ante un cambio de ejes la solución no se modificaría. Estas condiciones son de aplicación también para los pesos. 3.2.3. Elementos isoparamétricos Vamos a hacer un cambio de variable que nos llevará del dominio/ formulación global donde se define el problema (en coordenadas físicas) a otro dominio/ formulación local (coordenadas naturales) donde resulta más ventajosa la resolución del problema. En los casos en los que las matrices y vectores son muy complicados de calcular (dominios o ecuaciones diferenciales muy complejas ) se requiere un método de integración numérico y al hacer la adimensionalización del dominio que se verá a continuación la aplicación de cualquier método numérico se vuelve mucho más sencilla. Además, usaremos las mismas funciones de forma para aproximar la geometría y la función incógnita. Entonces: x= NE X Hi (ξ, η)xi (3.14) Hi (ξ, η)yi (3.15) Hi (ξ, η)ui (3.16) i=1 y= NE X i=1 u= NE X i=1 CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 32 Cuando se usan las mismas funciones de forma para la interpolación de la geometría y de la función incógnita estamos usando los denominados elementos isoparamétricos. 3.2.3.1. Unidimensionales Se toma un elemento 1D como el de la Figura 3.5 en el que se colocan los nodos en los puntos ξ1 = −1 y ξ2 = 1. Esta normalización será útil a la hora de calcular integrales posteriormente. Figura 3.5: Elemento unidimensional isoparamétrico. Las funciones de forma serán: H1 (ξ) = 1 (1 − ξ) 2 1 (1 + ξ) 2 siendo ξ la variable espacial que recorre el elemento, moviéndose en el intervalo [-1,1]. Sin más que sustituir se ve que se verifica (3.5). Este elemento puede estar localizado en cualquier punto del sistema de coordenadas físicas. Vamos a relacionar esta posición (x1 y x2 del elemento, con sus correspondientes valores u1 y u2 ) con las coordenadas naturales a través de (3.14): H2 (ξ) = x = H1 (ξ)x1 + H2 (ξ)x2 y por (3.16): u = H1 (ξ)u1 + H2 (ξ)u2 33 CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 3.2.3.2. Bidimensionales Como en el caso anterior, obtenemos las funciones de pequeño soporte para elementos triangulares y cuadriláteros. Elementos triangulares Un elemento triangular de 3 nodos como el de la Figura 3.6 permite definir unas funciones de forma tal que: H1 (ξ, η) = 1 − ξ − η H2 (ξ, η) = ξ H3 (ξ, η) = η con ξ y η las nuevas variables espaciales cuyo recorrido es el intervalo [0,1]. Se comprueba que las funciones así definidas cumplen (3.5). Figura 3.6: Elemento triangular en coordenadas naturales. 3 Nodos. Cuadriláteros Para un elemento cuadrilátero con 4 nodos como el de la Figura 3.7 se definen las funciones de forma: H1 (ξ, η) = 1 (1 − ξ)(1 − η) 4 (3.17) H2 (ξ, η) = 1 (1 + ξ)(1 − η) 4 (3.18) H3 (ξ, η) = 1 (1 + ξ)(1 + η) 4 (3.19) H4 (ξ, η) = 1 (1 − ξ)(1 + η) 4 (3.20) CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 34 Figura 3.8: Cuadrilátero en coordenadas físicas. Figura 3.7: Cuadrilátero en coordenadas naturales. En este caso, las variables espaciales que permiten definir la geometría del cuadrilátero varían en el intervalo [-1,1]. Sustituyendo los valores extremos de estas variables vemos que verifican (3.5). Siempre que se sea consistente con la numeración de los nodos (sentido horario o antihorario), se puede transformar un cuadrilátero con una forma y orientación cualquiera, como el de la Figura 3.8, en otro como el de la Figura 3.7, en coordenadas naturales, donde es más sencilla la resolución del problema. Las variables físicas quedan expresadas en función de las naturales a través de (3.14) y (3.15). Si seguimos el ejemplo del laplaciano, según (3.26) aparecerán términos con derivadas de las funciones de forma en x e y . Para el cálculo usando un elemento isoparamétrico, por la regla de la cadena, que se enuncia en (3.3), se tiene: ∂ ∂ ∂x ∂ ∂y = + ∂ξ ∂x ∂ξ ∂y ∂ξ ∂ ∂ ∂x ∂ ∂y = + ∂η ∂x ∂η ∂y ∂η Matricialmente: " ∂ ∂ξ ∂ ∂η # " = ∂x ∂ξ ∂x ∂η ∂y ∂ξ ∂y ∂η # ∂ ∂x ∂ ∂y CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 35 siendo: " J= ∂y ∂ξ ∂y ∂η ∂x ∂ξ ∂x ∂η # (3.21) la matriz jacobiana de la transformación. Nosotros vamos buscando la relación inversa, luego invertimos la matriz y despejamos: " # ∂ ∂x ∂ ∂y = J −1 ∂ ∂ξ ∂ ∂η (3.22) quedando por tanto completamente definidas las derivadas. Podría haberse tomado otra distribución de nodos: es típico tomar los llamados elementos lagrangianos, siendo estos elementos cuadrilátero de 8 o 9 nodos (hay un nodo en cada vértice, otro en el punto medio de cada lado y el noveno en el origen de coordenadas), cuyas funciones de forma quedan definidas por los polinomios de Lagrange: Iin (ξ) = (ξ − ξ0 ) · · · (ξ − ξi−1 )(ξ − ξi+1 ) · · · (ξ − ξn ) (ξi − ξ0 ) · · · (ξi − ξi−1 )(ξi − ξi+1 ) · · · (ξi − ξn ) Hij = Iin (ξ)Ijm (η) 3.3. 3.3.1. Ejemplos Planteamiento de un problema unidimensional. Formulación débil. Se plantea un problema cuya formulación fuerte es: 2 d u(x) − dx2 + u(x) = f (x) 0 ≤ x ≤ 1 f (x) = x u(0) = 0, u(1) = 0 (3.23) Al encontrarnos una derivada de segundo orden procedemos a la integración por partes del primer término del primer miembro. Dicho de otra manera, hacemos uso de la formulación débil del problema: ˆ1 Wi (− d2 û(x) + û(x) − f (x))dx = 0 dx2 0 ˆ1 0 ˆ1 ˆ1 dWi dû dû 1 dx − Wi | + Wi ûdx = Wi f (x)dx dx dx dx 0 0 0 CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 36 Vamos a tomar unas funciones de peso que cumplan Wi (0) = Wi (1) = 0, que anulan el segundo sumando, llegando a: ˆ1 dWi dû dx + dx dx ˆ1 0 ˆ1 Wi ûdx = 0 Wi f (x)dx 0 Tomando la división del dominio que se aprecia en la Figura 3.9 se puede proponer una serie de funciones elementales del tipo: Nie = he − (x − xi ) he Nje = x − xi he Figura 3.9: Dominio unidimensional. 5 Elementos. En la Figura 3.9 se aprecian los 5 elementos en que queda dividido el dominio al usar 6 nodos. P Si nuestra aproximación es u ≈ û = Nm am , en cada elemento (2 nodos por elementos) se tiene, como se vio anteriormente, que ue = ui Nie + uj Nje . Como pesos, Wie = Nie . Se obtiene, por tanto: x ˆi+1 e Kij = ( dNi dNj + Ni Nj )dx dx dx (3.24) xi x ˆi+1 Fie = f (x)Ni dx (3.25) xi El nuevo sistema algebraico al que se llega nos proporciona la solución (el P valor de la función) en los nodos. A partir de u ≈ û = Nm am conocemos el valor de u en todo el dominio. 37 CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS 3.3.2. Ejemplos de cálculo de matriz de rigidez A modo de ilustración, basándonos en la ecuación del Laplaciano, de aplicación en muchos campos de la física (permite, por ejemplo, modelar el flujo de un fluido incompresible, irrotacional y no viscoso) vamos a llegar a las expresiones de la matriz de rigidez K y calcularla en para un elemento triangular y un elemento rectangular (ejemplo extraído de [4]). Comenzamos determinando la expresión del residuo ponderado para el problema: ∂ 2 u(x, y) ∂ 2 u(x, y) + =0 ∂x2 ∂y 2 sujeto a: ( u = ū ∂u ∂n = q̄ en Γu en Γn Γu ∪ Γn = Γ Γu ∩ Γn = Ø De aplicar (2.28), se llega a que existe un término a aproximar cuya derivada es de orden 2: ˆ ˆ ˆ ∂2u ∂2u ∂u w( 2 + 2 )dΩ + (wu)dΓu + (w )dΓn = 0 ∂x ∂y ∂n Ω Γu Γn Integrando por partes el primer sumando, usando el Teorema de Green (ecuaciones (3.1) y (3.2)) se llega finalmente a una expresión de la matriz de rigidez tal que: ˆ ∂w ∂u ∂w ∂u Klm = ( + )dΩ (3.26) ∂x ∂x ∂y ∂y Ω Elemento triangular Aquí desarrollaremos la ecuación (3.26) para un elemento triangular. Sin más que sustituir u por su aproximación mediante las funciones de pequeño soporte y siendo los pesos w iguales a Hi se tiene que: ˆ e Klm = ∂w ∂u ∂w ∂u ( + )dΩ = ∂x ∂x ∂y ∂y ˆ ( Ωe Ωe + ∂H1 ∂y ∂H2 ∂y ∂H3 ∂y n ∂H1 ∂y ∂H2 ∂y ∂H1 ∂x ∂H2 ∂x ∂H3 ∂x ∂H1 ∂x ∂H3 ∂y o )dxdy ∂H2 ∂x ∂H3 ∂x 38 CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS Usando (3.7), (3.8) y (3.9) e integrando: k11 k12 e Klm = k21 k22 k31 k32 k11 = k13 k23 k33 1 [(x3 − x2 )2 + (y2 − y3 )2 ] 4A k12 = 1 [(x3 − x2 )(x1 − x3 ) + (y2 − y3 )(y3 − y1 )] 4A k13 = 1 [(x3 − x2 )(x2 − x1 ) + (y2 − y3 )(y1 − y2 )] 4A k22 = k23 = 1 [(x1 − x3 )2 + (y3 − y1 )2 ] 4A 1 [(x1 − x3 )(x2 − x1 ) + (y3 − y1 )(y1 − y2 )] 4A k33 = 1 [(x2 − x1 )2 + (y1 − y2 )2 ] 4A Elementos rectangulares. Procediendo de forma análoga: ˆ ∂w ∂u ∂w ∂u = ( + )dΩ = ( ∂x ∂x ∂y ∂y Ωe Ωe ˆ e Klm ∂H1 ∂y ∂H2 ∂y ∂H3 ∂y ∂H4 ∂y n ∂H1 ∂y ∂H2 ∂y ∂H1 ∂x ∂H2 ∂x ∂H3 ∂x ∂H4 ∂x ∂H1 ∂x ∂H2 ∂x ∂H3 ∂x ∂H4 ∂x + ∂H3 ∂y ∂H4 ∂y o )dxdy Explícitamente, el primer término, a modo de ejemplo, sería: ˆb ˆc 2 K11 = ( ∂H1 ∂H1 ∂H1 ∂H1 c2 + b2 + )dydx = ∂x ∂x ∂y ∂y 3bc −b −c De hecho, todos los términos de la diagonal tienen el mismo valor. El resto de términos: k12 = b2 − 2c2 6bc CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS k13 = − k14 = 39 b2 + c2 6bc c2 − 2b2 6bc k23 = k14 k24 = k13 k34 = k12 Los términos que faltan son conocidos al ser la matriz simétrica. Esta y otras propiedades serán objeto del apartado siguiente. 3.4. Propiedades de K y F A partir del problema ejemplo de la sección 3.23 se presentarán algunas propiedades de la matriz K y el vector F, introducidos en el apartado 3.2 y relacionados por la ecuación (3.4): Aditividad . La integral de una suma es igual a la suma de las integrales, luego la integral en el dominio Ω es igual a la suma de las integrales en los diferentes elementos Ωe . Se tiene, para la matriz de rigidez K : ˆ Kij = NE ( Ω X ∂Wi ∂Wi ∂Wj ∂Wj + )dΩ = ∂x ∂x ∂y ∂y i=1 ˆ NE ( Ωe X ∂Wie ∂Wie ∂Wje ∂Wje e + )dΩ = Kij ∂x ∂x ∂y ∂y i=1 Se puede proceder de forma análoga para el vector de cargas f (del ejemplo unidimensional, expresión (3.25)): ˆ1 fi = f (x)Wi dx = 0 NE ˆ X i=1 Ω e f (x)Wie dx = NE X Fie i=1 Tras calcular todas las integrales en los distintos elementos, estos se ensamblan para dar lugar al sistema completo en los grados de libertad definidos. K es una matriz banda. Consecuencia natural al usar funciones de pequeño soporte. Kij será distinto de 0 en los casos de elementos compartan un nodo, dando lugar a una banda de elementos distintos de 0 (fuera de la banda todos serán nulos). El ancho de la banda depende de la elección (numeración) de los nodos. Por ejemplo, podría tener una estructura de este tipo, para 5 nodos: CAPÍTULO 3. MÉTODO DE LOS ELEMENTOS FINITOS ∗ ∗ 0 0 0 40 ∗ 0 0 0 ∗ ∗ ∗ 0 ∗ ∗ ∗ 0 ∗ ∗ ∗ ∗ 0 0 ∗ ∗ En el caso de ejemplo, K es, además, simétrica. Al intercambiar los índices i y j en (3.24), se comprueba que Kij = Kji . Estas propiedades son de consideración a la hora de ahorrar tiempo de cálculo (programación del método). Capítulo 4 Sistema péndulo invertido 4.1. Descripción del sistema mecánico Este apartado se centra en la exposición y descripción del sistema sobre el que posteriormente se aplicarán los métodos numéricos anteriormente explicados: el péndulo invertido, extraído de [3]. El sistema del péndulo invertido es un sistema mecánico de dos grados de libertad, formado por una varilla de inercia I1 a la que está acoplada en su extremo superior un disco de inercia I2 y masa m. Los grados de libertad del sistema son el ángulo que forma la varilla con la vertical y el ángulo que forma un radio de referencia con la vertical, respectivamente (en la Figura 4.1, θ y ϕ). El objetivo es mantener la varilla vertical, empleando para ello un controlador que actúa sobre el disco: el giro del disco viene de la aplicación de un par motor v que es función de la posición de la varilla. 41 CAPÍTULO 4. SISTEMA PÉNDULO INVERTIDO 42 Figura 4.1: Esquema del sistema péndulo invertido. Las ecuaciones que gobiernan el problema son las de Lagrange: I1 + I2 I2 −mglsin(x) 0 Θ̈ + = v I2 I2 0 1 ϕ̈ Por simplicidad en la representación, se aplica el siguiente cambio de coordenadas: q1 = Θ q2 = Θ + ϕ con lo que se obtiene finalmente: I1 q¨1 + I2 q¨2 − mglsen(q1 ) = 0 I2 q¨2 = v que reescrito en forma matricial (despejando las variables q¨1 y q¨2 ): q¨1 −mglsen(θ)/I1 0 = + v q¨2 0 1 43 CAPÍTULO 4. SISTEMA PÉNDULO INVERTIDO 4.2. Descripción del controlador En [3] se propone el siguiente controlador para q1 , q2 : uc = ((GT · G)−1 )·(GT · (DV − Md · DVd )) − kd · (GT ) · (Md−1 · p) siendo: −1 1 p1 q˙1 p= = p2 q˙2 G= DV = mglsen(q1 ) " DVd = + kp (− γγ21 )(q2 − kp (q2 − γγ12 q1 ) mgl γ1 (−sen(q1 )) γ2 γ1 q1 # con γ1 , γ2 parámetros de control: γ1 = Md (1, 1) + Md (1, 2) γ2 = Md (2, 1) + Md (2, 2) es: y Md , mgl, kd y kp las ganancias de control. El sistema que ha de resolverse q˙1 p1 q̇2 p2 p˙1 = mglsen(q1 ) ṗ2 0 0 0 + −1 uc (q1 , q2 , p1 , p2 ) 1 Anteriormente ya introdujimos el vector DVd , que recoge las derivadas del potencial V (q1 , q2 ). Este potencial se calcula resolviendo la siguiente ecuación en derivadas parciales: γ1 ∂V ∂V + γ2 = −mglsen(q1 ) ∂q1 ∂q2 con γ1 < 0, γ2 = 6 0 y las condiciones de contorno: ( ∂2V | = k1 ∂q 2 (q1 ,q2 )=(0,0) 1 ∂2V ∂2V ∂q12 ∂q22 y cuya solución es: − ∂2V ∂q1 ∂q2 |(q1 ,q2 )=(0,0) = k2 k1 > 0 k2 > 0 (4.1) CAPÍTULO 4. SISTEMA PÉNDULO INVERTIDO V (q1 , q2 ) = 44 mgl kp γ2 cos(q1 ) + (q2 − q1 )2 γ1 2 γ1 Para las variables de control tomaremos los siguientes valores: ( γ1, = −1 γ2 = 4 mgl = 10, kp = kd = 1, siendo entonces nuestra ecuación: − ∂V ∂V +4 = −10sen(q1 ) ∂q1 ∂q2 (4.2) y su solución: V (q1 , q2 ) = −10cos(q1 ) + 0,5(q2 + 4q1 )2 (4.3) Ahora, las derivadas parciales buscadas: ∂V = −10sen(q1 ) + 4q2 + 16q1 ∂q1 ∂V = q2 + 4q1 ∂q2 4.3. Planteamiento de la resolución de la ecuación en derivadas parciales asociada al sistema péndulo Esta sección recoge el esquema planteado para resolver la ecuación en derivadas parciales que nace del problema del péndulo invertido. La ecuación a resolver y sus condiciones de contorno asociadas vienen dadas por (4.3) y (4.1) respectivamente. Estas condiciones de contorno son complicadas, por los que se propondrá una aproximación que facilite el cálculo. Definiéndose: α= mgl γ1 β= kp 2 γ= γ1 γ2 se reescribe la solución: V (q1 , q2 ) = αcos(q1 ) + β(q2 − γq1 )2 En la subsección 4.2 se tomaba para γ1 y γ2 los valores de −1 y 4 respectivamente, luego α < 0. Examinando la solución, vemos que es simétrica respecto del origen. En efecto: 45 CAPÍTULO 4. SISTEMA PÉNDULO INVERTIDO V (−q1 , −q2 ) = αcos(−q1 ) + β(−q2 + γq1 )2 = αcos(q1 ) + β(−1)2 (q2 − γq1 )2 = αcos(q1 ) + β(q2 − γq1 )2 Por tanto, solo es necesario resolver en un cuadrante. La Figura 4.2 muestra la solución real (obtenida para el intervalo −π ≤ x ≤ π, −π ≤ y ≤ π, por hacer las variables x e y referencia a ángulos). Figura 4.2: Solución Exacta de la ecuación diferencial. 4.3.1. Condiciones de contorno aproximadas Al tener (4.1) como condiciones de borde, no podremos usarlas para resolver el problema. Sin embargo, si nos apoyamos en ellas podemos inferir condiciones de borde válidas para el problema que estamos tratando, como por ejemplo: V (q10 , q2 ) = −αcos(q10 ) + β(q2 − γq10 )2 f rontera 1 V (q1f , q2 ) = −αcos(q1f ) + β(q2 − γq1f )2 f rontera 2 V (q1 , q20 ) = −αcos(q1 ) + β(q20 − γq1 )2 f rontera 3 V (q1 , q2f ) = −αcos(q1 ) + β(q2f − γq1 )2 f rontera 4 El dominio de integración será un cuadrilátero como el de la Figura 4.3 en la que se ha indicado las fronteras para mayor claridad. CAPÍTULO 4. SISTEMA PÉNDULO INVERTIDO 46 Figura 4.3: Recinto de integración para el MRP. Estamos ante una ecuación en derivadas parciales de primer orden, luego, de estas 4 condiciones de contorno solo podrán usarse 2. No obstante, en secciones posteriores se analizará el efecto de introducir un término corrector de segundo orden si fuese necesario, pudiendo por tanto usarse las 4 condiciones de borde y, presumiblemente, obtener una solución de mayor precisión. Por último, comentar que α y γ son datos del problema. El único parámetro de control es β: modificando su valor podemos hacer que en estas condiciones de contorno prime el término sinusoidal (β bajo) o el término parabólico (β alto). Capítulo 5 Método de los residuos ponderados De acuerdo a lo expuesto en la sección 2, concretamente en 2.1.3, se plantea la ecuación diferencial en la forma dada por (1.1) con las condiciones de contorno expresadas según la expresión (1.5). Por tanto, definiendo(x, y) = (q1 , q2 ): L() = γ1 ∂V ∂V + γ2 ∂x ∂y p = mglsen(x) M() = u ri = −φi siendo φi el valor de la condición de contorno de la frontera i. Tenemos que resolver el problema en el cuadrado definido por −π ≤ x ≤ π y−π ≤ y ≤ π , al representar ángulos las variables x e y. Sin embargo, empezaremos por un cuadrilátero de dimensiones genéricas x0 ≤ x ≤ xf e y0 ≤ y ≤ yf . Al comienzo de la siguiente sección haremos un análisis de la ecuación a resolver y sus condiciones de contorno que nos indicará la forma final del recinto de integración, es decir, el valor de los extremos x0 , xf , y0 , yf . Vamos a dividir el análisis según las funciones de peso elegidas sean las de Galerkin o las de Dirac. 5.1. 5.1.1. Galerkin Consideraciones previas Vamos a analizar las posibles aproximaciones que podemos proponer en busca de resultados intermedios que faciliten la resolución del problema. 47 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 5.1.1.1. 48 Necesidad de un dominio no simétrico En esta sección se demuestra la inviabilidad de usar funciones de peso de Galerkin en un dominio simétrico. Distinguimos dos posibles casos según el tipo de aproximación propuesta. Caso 1 Supongamos una aproximación del tipo: V̂ = ψ + M X Nm am m=1 con una función ψ capaz de aproximar las condiciones en los bordes (al ser un recinto bidimensional, el imponer el valor de la función en los 4 bordes no es en absoluto trivial; de hecho, no se ha encontrado un función que cumpla tales requisitos. No obstante, puede suponerse conocida un función ψ capaz de satisfacer dichas condiciones), y que las distintas funciones de aproximación Nm (x, y) sean nulas en los bordes, esto es: Nm (x0 , y) = 0 (5.1) Nm (xf , y) = 0 (5.2) Nm (x, y0 ) = 0 (5.3) Nm (x, yf ) = 0 (5.4) En este caso, estaríamos haciendo una propuesta como la desarrollada en la subsección 2.1.3.1, luego las expresiones de la matriz K y el vector f son (2.26) y (2.27) respectivamente: ˆ Klm = Wl L(Nm )dΩ 1≤l≤M y 1≤m≤M Ω ˆ fl = ˆ Wl L(ψ)dΩ Wl pdΩ + Ω 1≤l≤M Ω para un sistema Ka + f = 0. Vamos a desarrollar la expresión de K. Se recuerda que el método de Galerkin toma como funciones de peso las mismas que de aproximación, Wl = Nm . ˆ ˆ ˆ ∂Nm ∂Nm + γ2 )dxdy (5.5) Klm = Wl L(Nm )dΩ = Nl (γ1 ∂x ∂y Ω x y Dada la simetría respecto a x − y , vamos a quedarnos solo con el primer término de la integral (el análisis es análogo para el segundo término): CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS ˆ ˆ I1 = Nl γ1 x 49 ∂Nm dxdy ∂x y Para los términos diagonales (l = m) se tiene: ˆ ˆ ˆ ˆ ∂Nl ∂Nl Nl γ 1 I1 = dxdy = γ1 Nl dxdy ∂x ∂x x y x y Y por la regla de la cadena se deduce que: Nl ∂Nl 1 ∂ = (N 2 ) ∂x 2 ∂x l luego: ˆ ˆ γ1 1 ∂ (N 2 ) = 2 ∂x l 2 I1 = γ1 x ˆ ˆ x y e integrando respecto a x: γ1 I1 = 2 ∂ (N 2 )dxdy ∂x l y ˆ [Nl2 (xf , y) − Nl2 (x0 , y)]dy y pero según (5.1) y (5.2) esta integral es nula. Por la simetría existente en la ecuación (5.5) respecto a x-y, la segunda parte de la integral es nula también teniendo en cuenta (5.3) y (5.4). Entonces, se llegaría a una matriz cuya diagonal es nula y por tanto muy mal condicionada y dando lugar a malas soluciones. Caso 2 Ahora supongamos una aproximación del tipo: V̂ = M X Nm am m=1 ψ=0 Al desarrollo anterior habrá que añadirle el error que se produce en el borde. Esto ya se explicó en la subsección 2.1.3.2, y las expresiones de K y f son (2.29) y (2.30) respectivamente: ˆ ˆ Wl L(Nm )dΩ + Klm = Ω Ŵl M(Nm )dΓ 1≤l≤M Γ ˆ fl = ˆ Wl pdΩ + Ω Ŵl rdΓ Γ 1≤l≤M y 1≤m≤M CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 50 Ka + f = 0 Volvemos a analizar la primera de las integrales de la matriz K, que es exactamente la misma que se acaba de analizar, luego se llega de nuevo a: ˆ γ1 [Nl2 (xf , y) − Nl2 (x0 , y)]dy I1 = 2 y Ahora las funciones de prueba no tienen por qué ser nulas en los bordes, pero si analizamos en qué caso va a anularse esta integral, vemos que: Nl2 (xf , y) − Nl2 (x0 , y) = 0 → I1 = 0 Nl2 (xf , y) = Nl2 (x0 , y) Nl (xf , y) = ±Nl (x0 , y) al ser el dominio simétrico, x0 = −xf , por lo que: Nl (xf , y) = ±Nl (−xf , y) Es decir, siempre que las funciones de prueba sean pares o impares (la mayoría de las funciones típicas en los métodos numéricos) esta integral será nula y aportará a la matriz K únicamente ceros en la diagonal. Con esto concluimos la inviabilidad del uso de Galerkin en un recinto simétrico. Aunque en esta segunda forma de abordar el problema hay una segunda contribución a K, se ha comprobado que esta no llegaba a ser suficiente para llegar a un sistema bien condicionado y además se pierde completamente toda la información que contiene el operador L(), esto es, la ecuación diferencial a resolver (salvo la parte que no depende de V ): cualquier otra ecuación que cumpliese la misma estructura, es decir, que al aplicar Galerkin llevase a una integral doble de una función por su gradiente, daría el mismo resultado. Por ello y teniendo en cuenta el hecho de que, al tener la solución simetría respecto del origen, sólo es necesario calcularla en un cuadrante, el cálculo se llevará a cabo en recintos asimétricos en un único cuadrante. A partir de ahora, el dominio de integración será el primer cuadrante, donde 0 ≤ x ≤ xf e 0 ≤ y ≤ yf y las condiciones de contorno se impondrán sobre las de la frontera 1’ y 3’ definidas en la Figura 5.1. CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 51 Figura 5.1: Recinto de integración: primer cuadrante. Al ser muy difícil encontrar una función que cumple las condiciones de los bordes se ha pasado directamente a una aproximación del tipo: V̂ = M X Nm am m=1 ψ=0 por lo que: ˆ ˆ Klm = Wl L(Nm )dΩ + Ŵl M(Nm )dΓ Ω 1≤l≤M y 1≤m≤M Γ ˆ fl = ˆ Ŵl rdΓ Wl pdΩ + Ω 1≤l≤M Γ para Galerkin y Dirac. 5.1.1.2. Segundo Orden Vamos a introducir en la ecuación un término corrector de segundo orden y ver cómo afecta a las expresiones de K y f. Si añadimos un término de segundo orden, la ecuación resultante es: γ1 ∂V ∂V ∂2V ∂2V + γ2 + ( 2 + ) = −mglsen(x) ∂x ∂y ∂x ∂y con 1, variando respecto de la ecuación original únicamente en el operador diferencial L , que pasaría a ser: CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS L0 () = γ1 52 ∂() ∂() ∂ 2 () ∂ 2 () + γ2 + ( 2 + ) ∂x ∂y ∂x ∂y y, al ser lineal, puede expresarse como: L0 = L1 + L2 con L1 , L2 los operadores del primer y segundo orden respectivamente. Por tanto, no tenemos más que cambiar el operador L en las integrales (2.29) y (2.30) para ver la aportación del segundo orden: ˆ ˆ ˆ 0 Klm = Wl L (Nm )dΩ + Ŵl M(Nm )dΓ = Wl L1 (Nm )dΩ Ω Γ ˆ Ω ˆ ˆ Ŵl M(Nm )dΓ = Wl L2 (Nm )dΩ + + Ω Ord(1) Klm Wl L2 (Nm )dΩ + Ω Γ ˆ fl = ˆ Ŵl rdΓ Wl pdΩ + Ω Γ El vector f no cambia con respecto al problema de primer orden. Para K, hay que añadir un término al resultado obtenido del primer orden. En concreto: ˆ Ord(2) Klm Wl L2 (Nm )dΩ Ω Vamos a desarrollar esta integral: ˆ ˆ ˆ Wl L2 (Nm )dΩ = Wl L2 (Nm )dxdy = x Ω ˆ ˆ y Wl ( x ∂ 2 Nm ∂ 2 Nm )dxdy + ∂x2 ∂y y Vemos cómo las funciones de prueba deben ser ahora, además de integrables, derivables de clase C 2 . Para relajar un poco las condiciones sobre estas funciones se va a hacer uso de la formulación débil del problema usando el Teorema de Green introducido al final de la subsección 3.2.3.1. Entonces tendríamos: ˆ ˆ Wl x y Wl y ˆ ˆ x ˆ ˆ x ∂ 2 Nm dxdy = − ∂x2 ∂ 2 Nm dxdy = − ∂y 2 y y ˆ Wl ∂Nm nx dΓ ∂x Wl ∂Nm ny dΓ ∂y Γ ˆ ˆ x ∂Wl ∂Nm dxdy + ∂x ∂x ∂Wl ∂Nm dxdy + ∂y ∂y ˆ Γ 53 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS Sumando: ˆ ˆ ∂Wl ∂Nm dxdy+ ∂x ∂x − x y ˆ ∂Nm Wl nx dΓ− ∂x Γ ˆ ˆ Ord(2) Klm =− ( x ˆ ˆ x ˆ ∂Wl ∂Nm ∂Nm dxdy+ Wl ny dΓ = ∂y ∂y ∂y y ∂Wl ∂Nm ∂Wl ∂Nm + )dxdy + ∂x ∂x ∂y ∂y y Γ ˆ Wl ∂Nm dΓ ∂n (5.6) Γ La adición de este término de segundo orden permitiría forzar 4 condiciones de borde en lugar de 2. 5.1.1.3. Traslación del problema Lo último a tener en cuenta antes de empezar a proponer la solución es que es conveniente, por el tipo de aproximación llevada a cabo, realizar una traslación del problema. En efecto, analizando la solución se ve que en el origen el valor de esta es: kp γ2 mgl mgl cos(0) + (0 − 0)2 = = α = −10 γ1 2 γ1 γ1 La aproximación será de la forma û = a1 N1 + ... + aM NM . Si las Nm son distintos tipos de polinomios en x-y o funciones trigonométricas, estas se anularán en el origen dando, por lo tanto, una aproximación de valor 0 en el origen, cuando debería ser de -10, aunque la forma de la solución a la que se llegase fuese la correcta. Es decir, la solución será (pudiera ser) correcta pero desplazada en el eje Z un valor de 10. Para corregir esto, antes de empezar los cálculos, se añadirá a la solución y a las condiciones de contorno una constante de valor 10, que no hace más que trasladar la solución en el eje Z (se puede añadir una constante a la solución de una ecuación diferencial y esta seguirá siendo solución de la ecuación original). Con todo esto dicho, pasemos a buscar soluciones. V (0, 0) = 5.1.2. Solución con Galerkin Nuestro recinto de integración será el comprendido por 0 ≤ x ≤ π, 0 ≤ y ≤ π. Vamos a probar distintos tipos de funciones de aproximación, analizando los resultados y sacando las conclusiones pertinentes. Para cada tipo de función se hallará el error absoluto y relativo (en tanto por ciento), siendo estos la diferencia entre la solución exacta de la ecuación, que es (4.3) , y la aproximación, definidos como: Errorabsoluto = |Sol. exacta − Sol. aproximada| |(Sol. exacta − Sol. aproximada)| Sol. exacta El código que resuelve esta parte se encuentra en 8.1.1 dentro del Anexo. Errorrelativo = 100 ∗ 54 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 5.1.2.1. Aproximación mediante polinomios El primer tipo de función de aproximación empleada será: Nm = x m + y m empezando con m=1,2,3. En la Figura 5.2 se ve que la solución generada no tiene nada que ver con la solución real. Las figuras 5.3 y 5.4 recogen la distribución de ese error. Solucion Aproximada 2 0 -2 -4 -6 -8 -10 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 y 0 x Figura 5.2: Solución aproximada MRP. Suma de potencias de polinomios. 55 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS Error Relativo 10000 9000 8000 7000 6000 5000 4000 3000 2000 1000 0 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 0 y x Figura 5.3: Error relativo MRP. Suma de potencias de polinomios. Error Absoluto 150 100 50 0 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 y 0 x Figura 5.4: Error absoluto MRP. Suma de potencias de polinomios. No tiene mucho sentido el seguir aumentado M (número de funciones de aproximación) visto que la solución particular a la que se llega no tiene nada que ver con la que buscamos. CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 5.1.2.2. 56 Aproximación sinusoidal El segundo tipo de función propuesta es de tipo sinusoidal: Nm = cos(πxm)cos(πym) Las Figuras 5.5, 5.6 y 5.7 muestran la forma de la solución y los errores relativo y absoluto respectivamente. Figura 5.5: Solución aproximada MRP. Funciones sinusoidales. CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS Figura 5.6: Error Relativo MRP. Funciones sinusoidales. Figura 5.7: Error absoluto MRP. Funciones sinusoidales. De nuevo, vemos que no es la solución que buscamos. 57 58 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 5.1.2.3. Condiciones de contorno originales A la vista de estos resultados, cabe preguntarse qué puede está fallando. Se procede a revisar las condiciones de contorno originales del problema para buscar alguna pista. Las expresiones (4.1) muestran la dependencia de la solución con la segunda derivada. Esas condiciones vienen de imponer que el determinante del Hessiano sea positivo. Sabiendo que la solución es nula en el origen y teniendo en cuenta las condiciones sobre las derivadas se proponen las siguientes funciones de forma: N1 = x 2 N2 = x 4 N3 = y 2 N4 = xy Estas funciones cumplen las condiciones anteriormente citadas (valor nulo en el origen y condiciones de contorno originales). Entonces, usando las condiciones de contorno aproximadas y estas funciones de aproximación los resultados a los que se llega son los que aparecen en las Figuras 5.8, 5.9 y 5.10 Solucion Aproximada 150 100 50 0 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 y 0 x Figura 5.8: Solución aproximada MRP. Cumpliendo también condiciones de contorno originales. M=4. 59 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS Error Relativo 7 6 5 4 3 2 1 0 -1 -2 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 0 y x Figura 5.9: Error Relativo MRP. Cumpliendo también condiciones de contorno originales. M=4. Error Absoluto 2.5 2 1.5 1 0.5 0 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 y 0 x Figura 5.10: Error absoluto MRP. Cumpliendo también condiciones de contorno originales. M=4. Estas soluciones sí son las que buscamos. Ahora, el error relativo no pasa del 7 % y el absoluto no es mayor que 2.5. Vamos a añadir términos a nuestras 60 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS funciones de forma para ver si se consigue una aproximación más precisa. Las funciones que añadamos tiene que cumplir, por supuesto, las mismas restricciones. M=5 Añadiendo un término más, N5 = x6 , la solución mejora, como se ve en las Figuras 5.11, 5.12 y 5.13. Solucion Aproximada 150 100 50 0 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 0 y x Figura 5.11: Solución aproximada MRP. Cumpliendo también condiciones de contorno originales. M=5. Error Relativo 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 -0.1 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 y 0 x Figura 5.12: Error Relativo MRP. Cumpliendo también condiciones de contorno originales. M=5. 61 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS Error Absoluto 0.14 0.12 0.1 0.08 0.06 0.04 0.02 0 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 0 y x Figura 5.13: Error absoluto MRP. Cumpliendo también condiciones de contorno originales. M=5. El error relativo ahora es inferior al 1 % y el en términos absolutos la aproximación no difiere de la solución exacta en más de 0.14. M=6 Añadiendo una sexta función N6 = x8 : Solucion Aproximada 150 100 50 0 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 y 0 x Figura 5.14: Solución aproximada MRP. Cumpliendo también condiciones de contorno originales. M=6. 62 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS Error Relativo 0.04 0.035 0.03 0.025 0.02 0.015 0.01 0.005 0 -0.005 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 0 y x Figura 5.15: Error Relativo MRP. Cumpliendo también condiciones de contorno originales. M=6. Error Absoluto -3 x 10 5 4.5 4 3.5 3 2.5 2 1.5 1 0.5 0 3.5 3 3.5 2.5 3 2 2.5 1.5 2 1.5 1 1 0.5 0.5 0 y 0 x Figura 5.16: Error absoluto MRP. Cumpliendo también condiciones de contorno originales. M=6. A la vista de las imágenes vemos que la aproximación es muy buena. Aumentando el número de términos, el error disminuye: el método converge a una (la) solución del problema. No es necesario añadir el término de segundo orden CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 63 vista la calidad de los resultados. 5.1.3. Comentarios finales sobre el método de Galerkin La comparación se ha llevado a cabo en: 1 1 = 5M xf in 5M π puntos, es decir, a mayor grado de la función de interpolación, más puntos para comparar y mayor precisión. Fijándonos detenidamente, vemos que la forma de las funciones coincide con el desarrollo de Taylor de la solución: V (x, y) = αcos(x) + β(y − γx)2 ' α(1 − x4 x6 x2 + − + ...) + β(y − γx)2 2 4! 6! En efecto, si probásemos: N1 = x2 N2 = 1 − cos(x) N3 = y 2 N4 = xy teniendo en cuenta en N2 el 1 delante del coseno para que la función sea nula en el origen, se llega a la solución exacta. La conclusión es clara: para que se pueda aproximar correctamente es necesario, además trasladar la solución, que las funciones de forma: 1. Tengan un valor nulo en el origen. 2. Su segunda derivada tenga un valor constante en el origen (condiciones de contorno exactas). A fin de evitar los inconvenientes que presenta el método de Galerkin para la matriz K en la integral de dominio, proponemos en el próximo apartado una aproximación que sigue utilizando el método de Galerkin para la integral en el contorno mientras que para el dominio se utiliza el método de Dirac. 64 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 5.2. Dirac Como ya se comentó en la sección 2, se propone una aproximación del tipo: V̂ = M X Nm am m=1 por lo que: ˆ ˆ Klm = Wl L(Nm )dΩ + Ŵl M(Nm )dΓ Ω 1≤l≤M y 1≤m≤M Γ ˆ fl = ˆ Wl pdΩ + Ω Ŵl rdΓ 1≤l≤M Γ Ka + f = 0 5.2.1. Dirac en el dominio y Galerkin en el contorno Se tomará las funciones de peso para el dominio de Dirac y para el contorno de Galerkin. Esto puede hacerse al ser independientes los pesos usados en el dominio y en el contorno, como se explicó en 2.1.3.2 . Entonces, los pesos serán: Wl = δ(x − xl )δ(y − yl ) W l = Nm No tendremos aquí el problema de la paridad de las Nm por la estructura de la integral. Por las propiedades de la delta de Dirac expuestas en (2.10): ˆ Ŵl M(Nm )dΓ = L(Nm ) |x=xl ,y=yl + Wl L(Nm )dΩ + Klm = ˆ ˆ Ω Γ ˆ fl = Γ ˆ ˆ Ŵl rdΓ = p |x=xl ,y=yl + Wl pdΩ + Ω Nl Nm dΓ Γ Nl rdΓ Γ Cabe plantearse la siguiente pregunta: ¿dónde colocar las deltas de Dirac y cuántas son necesarias para una buena aproximación? La respuesta en profundidad a esta pregunta queda más allá de lo que se pretende estudiar en este trabajo. Se optará por hallar la solución del problema proponiendo sucesivas aproximaciones con un número creciente de términos y con distintas colocaciones de las deltas por el dominio y comentar los resultados. Las funciones de aproximación serán las que cumplan las condiciones expuestas en la subsección anterior. Se mostrará el resultado de usar otro tipo de funciones para verificar nuevamente la validez de la conclusión a la que se llegó. CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 65 Al conocer ya la forma de la solución, por no aportar nada nuevo y a efectos de reducir espacio, aquí solo presentaremos las gráficas de la distribución del error, que aportará la información necesaria sobre la convergencia de la aproximación a la solución. Al final de la sección se resumirán los resultados más relevantes en una tabla. Para Dirac, el código empleado se encuentra en el Anexo en 8.1.2. M=4 Comenzamos con M = 4, es decir: N1 = x 2 N2 = x4 N3 = y 2 N4 = xy y mostramos la distribución de deltas y su correspondiente error absoluto y relativo. Para el caso 1, tenemos una distribución de deltas como la de la Figura 5.17. Figura 5.17: Distribución deltas. Caso 1. Para el caso 2, la distribución es como la de la Figura 5.18 Figura 5.18: Distribución deltas. Caso 2. CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 66 Como se puede apreciar, el primer caso distribuye una delta por cada cuadrante (si se dividiese el dominio de integración en 4 cuadrantes imaginarios), mientras que la segunda coloca las deltas de forma equiespaciada sobre la recta y = x. Esta segunda distribución es más sencilla de implementar en función de M; en cambio, en el caso 1 hay que ir añadiendo cada término a mano en función del número de deltas que se deseen colocar. Caso 1 Para el caso 1, las distribuciones de error se recogen en las Figuras 5.19 y 5.20. Figura 5.19: Error absoluto Dirac. M=4. Caso 1. CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS Figura 5.20: Error relativo Dirac. M=4. Caso 1. Caso 2 Para el caso 2, las Figuras 5.19 y 5.20 muestran el error cometido. Figura 5.21: Error absoluto Dirac. M=4. Caso 2. 67 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 68 Figura 5.22: Error relativo Dirac. M=4. Caso 2. Se aprecia la influencia de la distribución de las deltas en el dominio en la precisión de la solución. Las que están distribuidas tal como en el caso 1 (más o menos uniformemente por el dominio) generan una aproximación con una mayor precisión, aunque, con 4 términos, la precisión es menor que la del método de Galerkin. M=5 Añadimos un nuevo término, N5 = x6 , para ver si mejora la solución. Hay que añadir una nueva delta al dominio, luego, siguiendo el tipo de distribución del caso M = 4: Para el caso 1, tenemos una distribución de deltas como la de la Figura 5.23. Figura 5.23: Distribución deltas M=5. Caso 1. Para el caso 2, la distribución es como la de la Figura 5.24 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 69 Figura 5.24: Distribución deltas M=5. Caso 2. Volvemos a separar los resultados para cada caso. Caso 1 Para el caso 1, las distribuciones de error se recogen en las Figuras 5.25 y 5.26. Figura 5.25: Error absoluto Dirac. M=5. Caso 1. CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS Figura 5.26: Error relativo Dirac. M=5. Caso 1. Caso 2 Para el caso 2, las Figuras 5.25 y 5.26 muestran el error cometido. Figura 5.27: Error absoluto Dirac. M=5. Caso 2. 70 CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 71 Figura 5.28: Error relativo Dirac. M=5. Caso 2. Como se dijo al principio de la sección, para verificar las condiciones impuestas sobre las funciones de prueba, se intenta una aproximación con: Nm = x m + y m que, como se vio anteriormente, no satisfacen dichas condiciones y con Galerkin no aportaban una buena solución. Las Figuras 5.29 y 5.30 muestran el error al que lleva una aproximación como esta. Figura 5.29: Error absoluto: Dirac con suma polinomios. CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS 72 Figura 5.30: Error relativo: Dirac con suma polinomios. 5.2.2. Comentarios finales sobre el método de Dirac Desde un principio se pudo ver que este método no es eficiente a la hora de la programación. Cada vez que se añaden términos han de colocarse en el dominio a mano en función de los puntos en los que se piensa (se sabe) que pueden favorecer una aproximación de mejor calidad, y la situación de estas deltas es clave para llegar a un resultado preciso. Además, dada M , es decir, la cantidad de funciones de interpolación (misma cantidad que deltas), la colocación de las deltas influye muchísimo en el resultado final. Por estos motivos el método es difícil de automatizar para un cálculo computacional y no es de gran interés práctico. 5.3. Resumen de resultados y conclusiones En este último apartado resumimos los resultados más importantes a los que hemos llegado y las conclusiones que de ellos se derivan. Las siguientes condiciones son fundamentales para poder llegar a resultados correctos: 1. Necesidad de una traslación de la solución para hacer coincidir el origen de coordenadas con el vértice del paraboloide solución. 2. Necesidad de que las funciones de aproximación cumplan las condiciones de contorno originales. Además, hay que recordar la inviabilidad de usar el método de Galerkin en un dominio simétrico. A partir de ahora, comparamos la precisión de cada aproximación. En la Tabla 5.1 se recogen los máximos de los errores absolutos y relativos según el tipo de aproximación empleada, para M=5. CAPÍTULO 5. MÉTODO DE LOS RESIDUOS PONDERADOS Dominio/Contorno Galerkin/Galerkin Dirac/Galerkin (caso 1) Dirac/Galerkin (caso 2) eabs 0.1316 0.05201 0.1176 73 erel ( %) 0.7321 0.3127 0.1663 Cuadro 5.1: Máximos del error para el MRP. M=5. De aquí se ve que sea cual sea el método se llega a una buena precisión(error menor al 1 % en términos relativos, que se pueden reducir aún más incrementando M); no es necesario añadir un término corrector de segundo orden. El método de Dirac tiene una precisión algo mayor, estando esta ligada a la forma en que se distribuyan estas deltas en el dominio: el caso 2 (reparto uniforme por el dominio) muestra un mejor resultado, para un mismo valor de M, en términos relativos. El hecho de poder colocar los pesos donde se desee permite colocar más allí donde el error sea mayor y con ello mejorar la aproximación; en cambio, el método de Galerkin no tiene noción alguna de lo que pasa en el dominio en el que está integrando (concentración local del error que se aprecia, con Galerkin, en el entorno del origen). Con Dirac, mediante prueba y error se podría ir mejorando la solución; no obstante, no es algo demasiado eficiente ni sistemático. Capítulo 6 Método de los elementos finitos En esta sección se muestra la aplicación del método de los elementos finitos al problema del péndulo invertido. Se analiza, como en el caso del MRP, únicamente un cuadrante (el primero, concretamente). El código utilizado se encuentra en el Anexo en 8.2.1. Allí se explica las diferencias que hay en el código según se quiera usar el planteamiento de primer o segundo orden. 6.1. 6.1.1. Primer Orden Planteamiento del residuo y mallado El problema se plantea de forma ligeramente distinta al MRP: se considera la integración del residuo en el dominio y posteriormente se aplican las condiciones de contorno. A partir de (2.30) y (2.29) y anulando las partes correspondientes al residuo en el borde (este se tendrá en cuenta más adelante al aplicar las condiciones de contorno) la matriz K y el vector f adoptan las siguientes expresiones: ˆ Klm = Wl L(Nm )dΩ Ω ˆ fl = Wl pdΩ Ω Ka + f = 0 El dominio de estudio es, como en la solución de residuos ponderados, un cuadrado en el que x e y varían entre 0 y π, el cual va a ser dividido en elementos cuadriláteros con 4 nodos por elemento, siendo N x y N y el número de nodos 74 75 CAPÍTULO 6. MÉTODO DE LOS ELEMENTOS FINITOS que hay en el eje x − y respectivamente. En la Figura 6.1 se muestra un ejemplo de mallado realizado para Nx = Ny = 3 (en todos los casos, N x será igual a N y), así como la numeración de nodos y elementos que se emplearán en nuestra formulación del problema. Figura 6.1: Mallado para MEF. 6.1.2. Matrices elementales. Elementos isoparamétricos Una vez planteado el residuo y hecho el mallado, debemos hallar las matrices elementales para luego ensamblarlas. La matriz elemental de un elemento e de coordenadas nodales (x1 , y1 ),(x2 , y1 ),(x1 , y2 ) y (x2 , y2 ) tiene la siguiente forma: ˆy2 ˆx2 e Klm Hl (x, y)(γ1 = ∂Hm (x, y) ∂Hm (x, y) + γ2 )dxdy ∂x ∂y (6.1) y1 x1 ˆy2 ˆx2 fle = Hl (x, y)mglsen(x)dxdy (6.2) y1 x1 Para facilitar la resolución de estas ecuaciones vamos a hacer un cambio de variable que nos llevará a un sistema de coordenadas paralelo al original pero con el origen en el centro del elemento e. Este cambio es: x0 = x − b y0 = y − c CAPÍTULO 6. MÉTODO DE LOS ELEMENTOS FINITOS 76 siendo: b = (x2 − x1 )/2 c = (y2 − y1 )/2, esto es, la base y la altura del elemento rectangular e (como vamos a tomar Nx = Ny y , el elemento será un cuadrado, por lo que b = c). Entonces, las funciones de forma son (3.10), (3.11), (3.12) y (3.13). Si unimos esto con (6.1) y (6.2) se llega a: ˆc ˆb Hl (x0 , y 0 )(γ1 e Klm = ∂Hm (x0 , y 0 ) ∂Hm (x0 , y 0 ) + γ2 )dx0 dy 0 0 ∂x ∂y 0 −c −b ˆc ˆb fle Hl (x0 , y 0 )mglsen(x0 )dx0 dy 0 = −c −b con lo que, al ser todos los elementos estos del mismo tipo (b = c en todos los elementos) y tener todos las mismas funciones de forma, estas integrales valen lo mismo para cada uno de ellos, por lo que solo se necesita calcular una y después ensamblarla en los grados de libertad que correspondan. Por ejemplificar la teoría que se explicó en el capítulo 3 se va a optar por una formulación con elementos isoparamétricos y a la aproximación de esta integral mediante cuadratura gaussiana. Para el cambio a isoparamétrico, comenzamos por calcular el jacobiano. De la ecuación (3.21), tenemos que calcular las siguientes derivadas parciales, teniendo en cuenta que x e y vienen dadas por (3.14), (3.15) y que las funciones de forma ahora son (3.17), (3.18), (3.19) y (3.20): ∂x = 0,25(−x1 (1 − η) + x2 (1 − η) + x3 (1 + η) − x4 (1 + η)) ∂ξ ∂y = 0,25(−y1 (1 − η) + y2 (1 − η) + y3 (1 + η) − y4 (1 + η)) ∂ξ ∂x = 0,25(−x1 (1 − ξ) − x2 (1 + ξ) + x3 (1 + ξ) + x4 (1 − ξ)) ∂η ∂y = 0,25(−y1 (1 − ξ) − y2 (1 + ξ) + y3 (1 + ξ) + y4 (1 − ξ)) ∂η Teniendo en cuenta que: x1 = x4 x2 = x3 y1 = y4 CAPÍTULO 6. MÉTODO DE LOS ELEMENTOS FINITOS 77 y2 = y3 b= x2 − x1 2 c= y2 − y1 2 El valor de las derivadas es: ∂x =b ∂ξ ∂y =0 ∂ξ ∂x =0 ∂η ∂y =c ∂η Por lo tanto, el valor del jacobiano es: b 0 J= 0 c cuyo determinante es: |J| = bc Se pueden obtener entonces las derivadas parciales de las funciones de aproximación respecto de x−y a partir de (3.22). Solo queda, tras haber ensamblado las matrices elementales, aplicar las condiciones de contorno. 6.1.3. Condiciones de contorno En esta sección vamos a comentar el algoritmo empleado para aplicar las condiciones de contorno, extraído de [4, página 55] . Conocido el valor de la función v en el nodo iCB , el algoritmo cambia el valor de f y K según: 0 fi = fi − v ∗ K(i, iCB ) Kii = 1 fiCB = v Además, el resto de elementos de K en la fila y columna i son nulos. Los elementos Kij que no pertenezcan a la fila o columna iCB quedan inalterados. 78 CAPÍTULO 6. MÉTODO DE LOS ELEMENTOS FINITOS Vamos a ilustrar el algoritmo empleado para aplicar las condiciones de contorno en un caso unidimensional, por sencillez, aunque la idea es la misma para el caso bidimensional que nos ocupa. El sistema al que se llega tras ensamblar las matrices y vectores elementales es del tipo: 1 k11 1 k21 0 0 .. . 0 0 0 1 k12 1 2 k22 + k11 2 k21 0 .. . 0 2 k12 2 3 k22 + k11 3 k21 .. . 0 0 0 u1 u2 u3 u4 .. . uN −2 uN −1 uN 0 0 0 = ··· ··· ··· ··· .. . 0 0 0 0 .. . 0 0 0 0 .. . N −2 N −1 N −1 k22 + k11 k12 N −1 N −1 N k21 k11 + k22 N 0 k21 f11 F1 F2 f21 + f12 2 3 F3 f2 + f1 F4 f23 + f14 .. = .. . . N −3 N −2 FN −2 fN + f −3 N −2 f1N −2 + f1N −1 FN −1 FN f2N −1 ··· ··· ··· 0 0 0 0 .. . ∗ 0 N k12 N k22 En los nodos extremos las condiciones de borde son conocidas, es decir, u1 = v1 y uN = vN , así que la forma final del sistema a resolver tras aplicar el algoritmo es: 1 0 0 0 .. . 0 0 0 0 1 2 k22 + k11 2 k21 0 .. . 0 2 k12 2 3 k22 + k11 3 k21 .. . 0 0 0 0 0 0 u1 u2 u3 u4 .. . uN −2 uN −1 uN ··· ··· ··· ··· .. . 0 0 0 0 .. . N −2 N −1 · · · k22 + k11 N −1 ··· k21 ··· 0 v1 1 F2 − v1 k21 F3 F4 = .. . FN −2 N FN −1 v − k12 vN 0 0 0 0 .. . N −1 k12 N −1 + k22 0 N k11 0 0 0 0 .. . ∗ 0 0 1 CAPÍTULO 6. MÉTODO DE LOS ELEMENTOS FINITOS 6.1.4. 79 Resultados En la Tabla 6.1 se muestran los errores máximos (relativos y absolutos) a los que se llega para este problema en función de Nx . En este caso, los puntos de comparación de la solución exacta y la aproximación son los propios nodos. Nx 10 20 30 eabs erel Nx eabs 7.9188e+12 5.5459e+12 40 1.9343e+11 9.3616e+11 1.0950e+12 50 1.2011e+10 4.0958e+10 1.8999e+11 60 5.3012e+10 Nx eabs erel 70 1.0102e+09 7.6096e+10 80 1.0935e+09 4.7790e+11 90 2.3571e+08 6.8935e+10 erel 1.2861e+12 8.2349e+10 6.9837e+12 Cuadro 6.1: Errores máximos para el MEF. Primer orden. Los resultados no son buenos (el método no converge), por lo que se procede a añadir el término de segundo orden. 6.2. Segundo Orden En la sección anterior se analizó el efecto del término de segundo orden en las expresiones, llegando a que era necesario añadir a la matriz de primer orden el término (5.6), quedándose inalterado el vector f. Vemos que aparece la siguiente integral de borde: ˆ ∂Nm Wl dΓ ∂n Γ Los bordes van a considerarse como elementos unidimensionales de 2 nodos: así, las funciones de aproximación serán del tipo: N1 (s) = 1 − s L s L siendo s la variable que recorre el borde y L la longitud del borde. Si miramos más detenidamente esta integral de borde, apoyándonos en la Figura 6.2 vemos que esta integral se anula siempre. N2 (s) = CAPÍTULO 6. MÉTODO DE LOS ELEMENTOS FINITOS 80 Figura 6.2: Normal en los bordes (MEF). Supongamos que esa integral se realiza en el borde 1, es decir, s = y , y el valor de la normal es n̂ = −ûx , teniendo ûx la dirección del eje x o lo que es lo mismo, la integral: ˆ ˆ ∂Nm ∂Nm (y) Wl dΓ = − Wl dy = 0 ∂n ∂x y Γ1 En cualquier borde habrá de derivarse con respecto a la otra variable, de la cual N no es función, luego la integral es nula. Por tanto: ˆ ˆ ˆ ∂Wl ∂Nm ∂Wl ∂Nm + )dxdy Klm = Wl L(Nm )dΩ − ( ∂x ∂x ∂y ∂y Ω x y ˆ fl = Wl pdΩ Ω Ka + f = 0 6.2.1. Resultados La Tabla 6.2 resume, de forma similar a como se hizo para el caso de primer orden, los errores en función de Nx para un valor de = 0,001: CAPÍTULO 6. MÉTODO DE LOS ELEMENTOS FINITOS N 10 20 30 eabs 9.5333e+10 3.7880e+10 1.4193e+10 erel N eabs 1.0603e+11 40 9.6413e+10 8.2615e+10 50 1.0464e+10 1.9697e+11 60 2.4895e+09 N eabs erel 70 9.7680e+09 9.2827e+11 80 5.1194e+08 3.2872e+11 90 1.0057e+09 3.6023e+11 81 erel 8.2626e+11 3.1374e+11 1.9146e+12 Cuadro 6.2: Errores máximos para el MEF. Segundo Orden. 6.3. Problemática asociada a la resolución mediante elementos rectangulares Vemos que el método no nos da la solución que buscamos. Examinando las matrices elementales k y la global del sistema K que se obtienen en los distintos cálculos, vemos que en la diagonal de la matriz global, en los nodos que no pertenecen a los bordes, que llamaremos a partir de ahora «interiores» en contraposición a los nodos del borde que denominaremos «exteriores», el valor que aparece es 0 (sea para el caso de primer o de segundo orden: la diferencia es únicamente en un pequeño número de nodos respecto del total), lo que suele ser un signo de mal condicionamiento. Ya hemos visto que tras la aplicación de las condiciones de contorno obtendremos una matriz K en la que habrá elementos de valor 1 en nodos exteriores (se tratará de bloques de matrices identidad si hay varios nodos pertenecientes al borde situados de forma consecutiva) y sumas de elementos pertenecientes a varias matrices k. Nos centramos por tanto en lo que pasa en los grados de libertad de los nodos interiores. El valor un elemento cualquiera de la diagonal K es igual a la traza de la matriz elemental k. En efecto, cualquier nodo interior está rodeado de 4 elementos. La aportación de cada elemento al nodo es el valor de uno de los elementos de la diagonal de la matriz elemental k (cada nodo aporta un valor distinto de la diagonal, luego la suma de los 4 es la suma de la diagonal de la matriz k), que, recordamos, es la misma para todos los elementos. Entonces, vamos a calcular el valor de esta suma con el fin de intentar averiguar por qué se anula. 4 X i=1 kii = 4 ˆb ˆc X Hi (x, y)(γ1 i=1 −b −c Separamos la integral en dos: ∂Hi (x, y) ∂Hi (x, y) + γ2 )dxdy ∂x ∂y CAPÍTULO 6. MÉTODO DE LOS ELEMENTOS FINITOS γ1 4 ˆb ˆc X i=1 −b −c 82 4 ˆb ˆc X ∂Hi (x, y) ∂Hi (x, y) dxdy + γ2 )dxdy Hi (x, y) Hi (x, y) ∂x ∂y i=1 −b −c Analizamos en primer lugar el primer sumatorio. Como ya se hiciera al desarrollar la ecuación en el MRP, vamos a usar la regla de la cadena. En efecto: Hi (x, y) 1 ∂ ∂Hi (x, y) = (H 2 (x, y)) ∂x 2 ∂x i por lo que: γ1 4 ˆb ˆc X i=1 −b −c 4 ˆb ˆc ∂Hi (x, y) γ1 X ∂ Hi (x, y) dxdy = (H 2 (x, y))dxdy ∂x 2 i=1 ∂x i −b −c γ1 2 ˆc X 4 (Hi2 (b, y) − Hi2 (−b, y))dy −c i=1 Donde hemos introducido el sumatorio dentro de la integral por la linealidad de la integral (la integral de la suma es igual a la suma de las integrales). Evaluamos las funciones de forma en los puntos (b, y), (−b, y) y elevamos al cuadrado para luego sustituir en la expresión que acabamos de hallar: H12 (b, y) = 0 H22 (b, y) = ( c−y 2 ) 2c H32 (b, y) = ( c+y 2 ) 2c H42 (b, y) = 0 H12 (−b, y) = ( c−y 2 ) 2c H22 (−b, y) = 0 H32 (−b, y) = 0 H42 (−b, y) = ( Calculamos: c+y 2 ) 2c CAPÍTULO 6. MÉTODO DE LOS ELEMENTOS FINITOS 83 4 X (Hi2 (b, y) − Hi2 (−b, y)) = 0 i=1 La segunda integral se analiza de forma análoga: Hi (x, y) γ2 4 ˆb ˆc X Hi (x, y) i=1 −b −c 1 ∂ ∂Hi (x, y) = (H 2 (x, y)) ∂x 2 ∂x i 4 ˆb ˆc ∂ ∂Hi (x, y) γ2 X )dxdy = (H 2 (x, y))dxdy ∂y 2 i=1 ∂x i −b −c γ2 2 ˆb X 4 (Hi2 (x, c) − Hi2 (x, −c))dx −b i=1 Para calcular el sumatorio necesitamos los siguientes valores: H12 (x, c) = 0 H22 (x, c) = 0 H32 (x, c) = ( b+x 2 ) 2b H42 (x, −c) = ( b−x 2 ) 2b H12 (x, −c) = ( b−x 2 ) 2b H22 (x, −c) = ( b+x 2 ) 2b H32 (x, −c) = 0 H42 (x, −c) = 0 Entonces: 4 X (Hi2 (x, c) − Hi2 (x, −c)) = 0 i=1 Se demuestra así que la suma de los elementos de la diagonal de la matriz elemental es nula y por tanto, la matriz global tendrá en su diagonal un 1 si CAPÍTULO 6. MÉTODO DE LOS ELEMENTOS FINITOS 84 el nodo es exterior y un 0 si se trata de un nodo interior, lo que hace que el condicionamiento de la matriz sea malo. Otra forma más corta de demostrarlo es notar que la función: f (x, y) = 4 X Hi (x, y)(γ1 i=1 ∂Hi (x, y) ∂Hi (x, y) + γ2 ) ∂x ∂y es impar (puede hacerse fácilmente con alguna herramienta de cálculo simbólico) y se está integrando en un recinto simétrico, luego el valor de la integral es 0. 6.4. Conclusiones En esta sección hemos visto que la aplicación del MEF a la ecuación diferencial que estamos tratando, usando elementos rectangulares, no da los resultados esperados. Hemos demostrado que con las funciones de aproximación típicas en formulaciones de elementos finitos usando elementos rectangulares, dada la ecuación diferencial que pretendemos aproximar y la geometría del dominio que estamos tratando, llegamos a un sistema mal condicionado, luego ha de descartarse este tipo de elementos a la hora de resolver el problema. Podemos relacionar estos resultados con los resultados obtenidos aplicando el MRP. La semejanza entre ambos problemas es notoria: en el caso de que se seleccionase un único elemento, las integrales a las que se llega son las mismas en ambos métodos (MRP con Galerkin como pesos), luego, si ya vimos que eran necesarias unas ciertas condiciones sobre las funciones de forma para que se obtuviese la solución correcta, es de esperar que las funciones de aproximación en elementos finitos tengan que cumplir condiciones semejantes. Capítulo 7 Trabajo futuro En esta última sección se enumeran posibles ampliaciones de este proyecto.Por el lado de los residuos ponderados: 1. Estudio más exhaustivo de la influencia de la distribución de las deltas de Dirac en el dominio. 2. Estudio de caso en el que se use únicamente deltas de Dirac como pesos (para dominio y contorno). 3. En cuanto al código, abandonar la herramienta simbólica y usar cuadraturas (por ejemplo, dlbquad, cuadratura para integrales dobles) reduciendo así el tiempo de cálculo sin sacrificar en exceso la precisión. Para elementos finitos: Como se indicó al final de la sección anterior, cabe esperar que las funciones de aproximación deban satisfacer ciertas condiciones. Siguiendo con las ideas del MRP, podría implementarse el MEF usando las funciones de aproximación que eran allí apropiadas. En la sección 3.2.1.2 se describe el procedimiento para, usando este tipo de aproximación, es decir, u = a1 ·1 + a2 x2 + a3 y 2 + a4 xy obtener las funciones de pequeño soporte correspondientes para llegar a un ensamblado sencillo. En este punto, hay que tener en cuenta una de las condiciones que deben cumplir el polinomio de interpolación: completitud. El polinomio debe ser completo hasta el grado máximo de este, luego, se podría usar un elemento cuadrilátero de 8 nodos y obtener las funciones de pequeño soporte a partir de u = a1 ·1 + a2 x + a3 y + a4 xy + a5 x2 + a6 y 2 + a7 xy 2 + a8 x2 y 85 CAPÍTULO 7. TRABAJO FUTURO 86 Es sencillo encontrar en la bibliografía las expresiones de las Hm para elementos isoparamétricos lagrangianos de 9 nodos o elementos de 8 nodos, llamados serendípitos (en el capítulo 3 ya se explicó cómo obtener las funciones de pequeño soporte Hm a partir de su definición). Capítulo 8 Anexo Presentamos los códigos, comentados, que se han escrito para este trabajo. 8.1. Código para residuos ponderados 8.1.1. Galerkin Definición del dominio y datos del problema (parámetros de control), así como definición de x e y como variables simbólicas: 1 2 3 clear all clc close all 4 5 6 7 8 9 syms x y r e a l x0 =0; x f i n=p i ; y0 =0; y f i n=x f i n ; 10 11 12 13 14 15 16 gamma1=−1; gamma2=4; gamma=gamma2/gamma1 ; beta =0.5; mgl =10; a l f a=mgl/gamma1 ; Condiciones de contorno (y su traslación), y de ψ, L(ψ) y p: 87 CAPÍTULO 8. ANEXO 1 88 c c o n t =[ a l f a ∗ c o s ( x0 )+b e t a ∗ ( y−gamma∗ x0 ) ^2 , a l f a ∗ c o s ( x f i n )+ b e t a ∗ ( y−gamma∗ x f i n ) ^2 , a l f a ∗ c o s ( x )+b e t a ∗ ( y0−gamma∗x ) ^2 , a l f a ∗ c o s ( x )+b e t a ∗ ( y f i n −gamma∗x ) ^ 2 ] ’ ; 2 3 %% T r a s l a c i ó n 4 5 c c o n t=c c o n t +10; 6 7 8 9 P s i =0; L p s i =0; p=mgl∗ s i n ( x ) ; Definición de las funciones de aproximación. Esta parte varía según las funciones de aproximación elegidas: 1 %% Aproximación s i n u s o i d a l 2 3 4 5 f o r m=1:M N(m)=c o s ( p i ∗x∗m) ∗ c o s ( p i ∗y∗m) ; end 6 7 %% Aproximación por suma de p o l i n o m i o s 8 9 10 11 f o r m=1:M N(m)=x^m+y^m; end 12 13 %% Aproximación t e n i e n d o en c u e n t a l a s c o n d i c i o n e s de c o n t o r n o o r i g i n a l e s ( e l e g i r M) 14 15 16 17 18 19 20 21 N( 1 )=x ^ 2 ; N( 2 )=x ^ 4 ; N( 3 )=y ^ 2 ; N( 4 )=x∗y ; N( 5 )=x ^ 6 ; N( 6 )=x ^ 8 ; M=l e n g t h (N) ; Definición de pesos W y del operador L(Nm ): 1 W=N; %% Método de G a l e r k i n 2 3 LN=gamma1∗ d i f f (N, x )+gamma2∗ d i f f (N, y ) ; CAPÍTULO 8. ANEXO Integrales (dominio): 1 2 3 4 5 6 7 8 9 10 f o r l =1:M f o r m=1:M i n t e g r a d o r k=W( l ) ∗LN(m) ; i n t x=i n t ( i n t e g r a d o r k , x , x0 , x f i n ) ; Kdom( l ,m)=i n t ( i n t x , y , y0 , y f i n ) ; end i n t e g r a d o r f=W( l ) ∗ ( L p s i+p ) ; i n t x=i n t ( i n t e g r a d o r f , x , x0 , x f i n ) ; fdom ( l )=−i n t ( i n t x , y , y0 , y f i n ) ; end Para la frontera: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 x f r o n t =[x0 , x f i n , x , x ] ; y f r o n t =[y , y , y0 , y f i n ] ; r=−c c o n t ; f o r l =1:M f o r m=1:M s =1; syms x y r e a l x=x f r o n t ( s ) ; integrandoK=s u b s (W( l ) ∗N(m) ) ; Kf1 ( l ,m)=i n t ( integrandoK , y , y0 , y f i n ) ; syms x y r e a l s =3; y=y f r o n t ( s ) ; integrandoK=s u b s (W( l ) ∗N(m) ) ; Kf3 ( l ,m)=i n t ( integrandoK , x , x0 , x f i n ) ; 16 end syms x y r e a l s =1; i n t e g r a d o r f f r o n t=W( l ) ∗ ( P s i+r ( s ) ) ; x=x f r o n t ( s ) ; f f r o n t 1 ( l )=−i n t ( s u b s ( i n t e g r a d o r f f r o n t ) , y , y0 , y f i n ) ; 17 18 19 20 21 22 23 24 25 26 27 28 29 end syms x y r e a l s =3; i n t e g r a d o r f f r o n t=W( l ) ∗ ( P s i+r ( s ) ) ; y=y f r o n t ( s ) ; f f r o n t 3 ( l )=−i n t ( s u b s ( i n t e g r a d o r f f r o n t ) , x , x0 , x f i n ) ; 89 CAPÍTULO 8. ANEXO 90 Suma de las matrices calculadas en las dos partes anteriores y resolución del sistema algebraico: 1 2 Kf=Kf1+Kf3 ; f f r o n t =f f r o n t 1+f f r o n t 3 ; 3 4 5 6 7 K=Kdom+Kf ; f=f f r o n t+fdom ; a=K\ f ’ ; syms x y r e a l Soluciones, comparación y dibujo de resultados: 1 %% S o l u c i o n e s e x a c t a y aproximada 2 3 4 Exacto=a l f a ∗ c o s ( x )+b e t a ∗ ( y−gamma∗x ) ^2+10; S o l =( P s i+N∗a ) ; 5 6 7 8 9 10 %% Puntos de comparación xdom=x0 : ( x f i n −x0 ) / ( 5 ∗ x f i n ∗M) : x f i n ; ydom=y0 : ( y f i n −y0 ) / ( 5 ∗ y f i n ∗M) : y f i n ; n=l e n g t h ( xdom ) ; m=l e n g t h ( ydom ) ; 11 12 13 14 15 16 17 18 19 20 21 22 f o r i =1:n x=xdom ( i ) ; f o r j =1:m y=ydom ( j ) ; ExactoNum ( i , j )=s u b s ( Exacto ) ; SolNum ( i , j )=s u b s ( S o l ) ; E r r o r _ a b s o l u t o ( i , j )=abs ( ExactoNum ( i , j )−SolNum ( i , j ) ) ; E r r o r _ R e l a t i v o ( i , j ) =(ExactoNum ( i , j )−SolNum ( i , j ) ) / ( ExactoNum ( i , j )+e p s ) ∗ 1 0 0 ; end end 23 24 25 ErrorMax_rel =max(max( abs ( E r r o r _ R e l a t i v o ) ) ) ErrorMinimo_rel =min ( min ( abs ( E r r o r _ R e l a t i v o ) ) ) ; 26 27 28 ErrorMax_abs =max(max( abs ( E r r o r _ a b s o l u t o ) ) ) ErrorMinimo_abs =min ( min ( abs ( E r r o r _ a b s o l u t o ) ) ) ; 29 30 close all CAPÍTULO 8. ANEXO 91 31 32 33 34 35 36 figure (1) s u r f ( xdom , ydom , E r r o r _ a b s o l u t o ) xlabel ( ’x ’ ) ylabel ( ’y ’ ) t i t l e ( ’ E r r o r Absoluto ’ ) 37 38 39 40 41 42 figure (2) s u r f ( xdom , ydom , E r r o r _ R e l a t i v o ) xlabel ( ’x ’ ) ylabel ( ’y ’ ) t i t l e ( ’ Error Relativo ’ ) 43 44 45 46 47 48 figure (3) s u r f ( xdom , ydom , SolNum ) xlabel ( ’x ’ ) ylabel ( ’y ’ ) t i t l e ( ’ S o l u c i o n Aproximada ’ ) 49 50 51 52 53 54 figure (4) s u r f ( xdom , ydom , ExactoNum ) t i t l e ( ’ S o l u c i o n Exacta ’ ) xlabel ( ’x ’ ) ylabel ( ’y ’ ) 55 56 g r i d on 8.1.2. Dirac Aquí solo se introducen las partes del código que sean distintas al de Galerkin (colocación de las deltas e integrales en el dominio). Colocación de las deltas en el dominio (en función de M y según sea el caso 1 o 2). 1 2 3 4 5 6 7 8 9 10 %% Caso 1 ( i n d e p e n d i e n t e m e t e d e l v a l o r de M) xdom=x0 : ( x f i n −x0 ) / (M−1) : x f i n ; ydom=y0 : ( y f i n −y0 ) / (M−1) : y f i n ; %% Caso 2 . E l e g i r e n t r e M=4 o M=5 M=4 xdom=[ x f i n / 3 , x f i n / 3 , 2 ∗ x f i n / 3 , 2 ∗ x f i n / 3 ] ; ydom=[ y f i n / 3 , 2 ∗ y f i n / 3 , y f i n / 3 , 2 ∗ y f i n / 3 ] ; M=5 xdom=[ x f i n / 3 , x f i n / 3 , 2 ∗ x f i n / 3 , 2 ∗ x f i n / 3 , x f i n / 2 ] ; ydom=[ y f i n / 3 , 2 ∗ y f i n / 3 , y f i n / 3 , 2 ∗ y f i n / 3 , y f i n / 2 ] ; CAPÍTULO 8. ANEXO 92 11 12 %% R e p r e s e n t a c i ó n de l a s d e l t a s en e l dominio 13 14 x d i r a c=xdom ; y d i r a c=ydom ; 15 16 17 18 19 figure (5) p l o t ( xdirac , ydirac , ’ ro ’ ) xlabel ( ’x ’ ) % ylabel ( ’y ’) g r i d on Integrales (dominio): 1 2 3 4 5 6 7 8 9 10 f o r l =1:M f o r m=1:M i n t e g r a d o r k=W( l ) ∗LN(m) ; i n t x=i n t ( i n t e g r a d o r k , x , x0 , x f i n ) ; Kdom( l ,m)=i n t ( i n t x , y , y0 , y f i n ) ; end i n t e g r a d o r f=W( l ) ∗ ( L p s i+p ) ; i n t x=i n t ( i n t e g r a d o r f , x , x0 , x f i n ) ; fdom ( l )=−i n t ( i n t x , y , y0 , y f i n ) ; end El resto del código es el mismo. Estos dos bloques se insertan después de la definición de las funciones Nm (sustituyendo al de las integrales en el dominio de Galerkin). 8.2. Código para elementos finitos Se expondrá, a fin de no ocupar espacio en exceso, el código referente al segundo orden, haciendo los comentarios necesarios para su adaptación al primer orden. 8.2.1. Segundo orden Definición de los parámetros de control, del dominio y de variables necesarias posteriormente (v. gr. número de nodos, grados de libertad por elemento, etc.). 1 2 3 clear all clc close all 4 5 Nx=3; CAPÍTULO 8. ANEXO 6 7 8 9 10 93 Ny=Nx ; n e l =(Nx−1) ∗ (Ny−1) ; %% Número de e l e m e n t o s n n e l =4; %% Nodos por e l e m e n t o n g d l =1; %% Grados de l i b e r t a d por nodo nnodos=Nx∗Ny ; %% Número de nodos 11 12 13 14 15 %% V a l o r e s u s a d o s para l a c u a d r a t u r a de Gauss n g l x =3; n g l y =3; n g l =3; 16 17 18 19 20 21 22 23 24 25 %% Grados de l i b e r t a d d e l s i s t e m a g d l s i s t=nnodos ∗ n g d l ; g d l c a d a e l e m e n t o=n n e l ∗ n g d l ; gamma1=−1; gamma2=4; gamma=gamma2/gamma1 ; beta =0.5; mgl =10; a l f a=mgl/gamma1 ; 26 27 28 29 30 31 %% L í m i t e s d e l dominio x0 =0; y0 =0; x f i n=p i ; y f i n=x f i n ; 32 33 34 35 36 37 %% I n t r o d u c c i ó n c o o r d e n a d a s nodos ( g l o b a l e s ) x=x0 : ( x f i n −x0 ) / (Nx−1) : x f i n ; y=y0 : ( y f i n −y0 ) / (Ny−1) : y f i n ; n=l e n g t h ( x ) ; m=l e n g t h ( y ) ; Coordenadas nodales y conectividad (qué nodos corresponden a qué elemento). Es más sencillo entender esta parte del código si se tiene delante la distribución de nodos (Figuras 6.1 y 3.4): 1 2 3 4 5 6 7 8 %% Coordenadas n o d a l e s %% V a r i a b l e s para r e c o r r e r l o s nodos en %% h o r i z o n t a l ( h ) y v e r t i c a l ( v ) h=1; v=1; f o r i =1: nnodos f o r j =1:2; i f j==1 94 CAPÍTULO 8. ANEXO c o o r d f i s i c a s ( i , j )=x ( h ) ; h=h+1; else c o o r d f i s i c a s ( i , j )=y ( v ) ; 9 10 11 12 13 14 %% S i l l e g a a un nodo m ú l t i p l o de Nx ( e s t a r á en e l extremo d e r e c h o ) l l e v a h a 1 para poner l a s c o o r d e n a d a s d e l s i g u i e n t e nodo en e l borde i z q u i e r d o ( x0 ) 15 i f h==Nx+1 h=1; v=v+1; end 16 17 18 19 20 21 22 23 end end end 24 25 %% C o n e c t i v i d a d 26 27 28 n i v e l =0; c o n e c t i v i d a d=z e r o s ( n e l , 4 ) ; 29 30 %% C á l c u l o de qué nodos c o r r e s p o n d e n a cada e l e m e n t o . 31 32 33 34 35 36 37 38 39 f o r i =1: n e l i f i<=Nx−1 n i v e l =0; %% E s t a r í a en l a f r o n t e r a 3 ( l a " b a s e " ) else n i v e l=f l o o r ( i / (Nx−1) ) ; i f rem ( i , ( Nx−1) )==0 end end 40 41 42 43 44 45 46 47 48 49 50 51 f o r j =1:4 k=rem ( i , ( Nx−1) ) ; i f k==0 k=(Nx−1) ; end i f j==1 c o n e c t i v i d a d ( i , j )=k+n i v e l ∗Nx ; e l s e i f j==2 c o n e c t i v i d a d ( i , j )=k+n i v e l ∗Nx+1; e l s e i f j==3 c o n e c t i v i d a d ( i , j )=k+n i v e l ∗Nx+(Nx+1) ; CAPÍTULO 8. ANEXO else 52 53 54 55 56 end end end 95 c o n e c t i v i d a d ( i , j )=k+n i v e l ∗Nx+Nx ; A continuación, las condiciones de borde: se definen los nodos del contorno (gdlborde) y el valor de la función en dichos nodos (valorborde): 1 2 3 4 5 6 7 8 9 10 %% CONDICIONES CONTORNO %% Problema de segundo orden . 4 c o n d i c i o n e s de c o n t o r n o %% Esquema de l o s nodos en cada borde %−−−−−−−−− %| | %| | %| | %−−−−−−−−− %% Asi s e ve que nodos c o r r e s p o n d e n a cada borde %% ( para no poner 2 v e c e s l a s e s q u i n a s ) 11 12 13 n o d o s b a s e =1:Nx ; n o d o s l a t i z q=Nx+1:Nx : Nx∗ (Ny−1) ; 14 15 %% A comentar , s i e s p r i m e r orden , e s t a s dos l i n e a s 16 17 18 n o d o s l a t d e r =2∗Nx : Nx : Nx∗ (Ny−1) ; n o d o s a r r i b a =(Ny−1)∗Nx+ 1 : 1 :Ny∗Nx ; 19 20 %% Para p r i m e r orden 21 22 nodosborde =[ n o d o s b a s e n o d o s l a t i z q ] ; 23 24 %% Para segundo orden 25 26 27 28 29 30 31 32 33 34 35 nodosborde =[ n o d o s b a s e n o d o s l a t i z q n o d o s l a t d e r n o d o s a r r i b a ]; h=1; % Para i r r e c o r r i e n d o l o s nodos de cada borde j =1; % Para i r r e c o r r i e n d o l o s nodos de cada borde f o r i=n o d o s b a s e g d l b o r d e ( j )=i ; v a l o r b o r d e ( j )=a l f a ∗ c o s ( x ( h ) )+b e t a ∗ ( y0−gamma∗x ( h ) ) ^ 2 ; h=h+1; j=j +1; end v=2; CAPÍTULO 8. ANEXO 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 96 f o r i=n o d o s l a t i z q g d l b o r d e ( j )=i ; v a l o r b o r d e ( j )=a l f a ∗ c o s ( x0 )+b e t a ∗ ( y ( v )−gamma∗ x0 ) ^ 2 ; v=v+1; j=j +1; end v=2; f o r i=n o d o s l a t d e r g d l b o r d e ( j )=i ; v a l o r b o r d e ( j )=a l f a ∗ c o s ( x f i n )+b e t a ∗ ( y ( v )−gamma∗ x f i n ) ^2; v=v+1; j=j +1; end h=1; f o r i=n o d o s a r r i b a g d l b o r d e ( j )=i ; v a l o r b o r d e ( j )=a l f a ∗ c o s ( x ( h ) )+b e t a ∗ ( y f i n −gamma∗x ( h ) ) ^2; h=h+1; j=j +1; end Para el primer orden, bastaría con comentar los bucles referentes a los nodos de la frontera 2 y 4 (los bucles de nodoslatder y nodosarriba en el trozo de código anterior). Ahora, la parte referida al cálculo de las integrales (mediante cuadratura Gaussiana). Para el primer orden no hay más que igualar e (variable que representa a ) a 0: 1 2 3 4 5 6 7 8 9 10 %I n i c i a l i z a c i ó n m a t r i c e s y v e c t o r e s f f =z e r o s ( s d o f , 1 ) ; kk=z e r o s ( s d o f , s d o f ) ; [ p o i n t 2 , w e i g h t 2 ]= f e g l q d 2 ( nglx , n g l y ) ; nd=z e r o s ( 1 , 2 ) ; xcoord=z e r o s ( 1 , 4 ) ; ycoord=z e r o s ( 1 , 4 ) ; e =10^(−3) ; k=z e r o s ( edo f , e d o f ) ; f=z e r o s ( 1 , e d o f ) ; 11 12 13 14 15 %%Calculamos l a m a t r i z para e l p r i m e r e l e m e n t o f o r i =1: n n e l %Para l o s 4 nodos d e l e l e m e n t o nd ( i )=c o n e c t i v i d a d ( i e l , i ) ; xcoord ( i )=c o o r d f i s i c a s ( nd ( i ) , 1 ) ; 97 CAPÍTULO 8. ANEXO 16 17 end ycoord ( i )=c o o r d f i s i c a s ( nd ( i ) , 2 ) ; 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 %%I n t e g r a c i o n numerica para l a m a t r i z e l e m e n t a l b=( xcoord ( 2 )−xcoord ( 1 ) ) / 2 ; f o r i n t x =1: n g l x x=p o i n t 2 ( i n t x , 1 ) ; wtx=w e i g h t 2 ( i n t x , 1 ) ; f o r i n t y =1: n g l y y=p o i n t 2 ( i n t y , 2 ) ; wty=w e i g h t 2 ( i n t y , 2 ) ; [ shape , dhdr , dhds ]= f e i s o q 4 ( x , y ) ; j a c o b 2=f e j a c o b 2 ( nnel , dhdr , dhds , xcoord , ycoord ) ; d e t j a c o b=d e t ( j a c o b 2 ) ; i n v j a c o b=i n v ( j a c o b 2 ) ; [ dhdx , dhdy]= f e d e r i v 2 ( nnel , dhdr , dhds , i n v j a c o b ) ; f o r i =1: e d o f f o r j =1: e d o f k ( i , j )=k ( i , j )+shape ( i ) ∗ (gamma1∗dhdx ( j )+gamma2∗dhdy ( j )+e ∗ ( dhdx ( i ) ∗dhdx ( j )+dhdy ( i ) ∗dhdy ( j ) ) ) ∗ d e t j a c o b ∗ wtx∗wty ; end f ( i )=f ( i )+mgl∗ shape ( i ) ∗ s i n ( b∗x ) ∗ d e t j a c o b ∗wtx∗wty ; end end end 40 41 f o r i e l =1: n e l %para t o d o s l o s e l e m e n t o s 42 43 44 45 46 47 48 49 f o r i =1: n n e l %Para l o s 4 nodos d e l e l e m e n t o nd ( i )=c o n e c t i v i d a d ( i e l , i ) ; end i n d e x=f e e l d o f ( nd , nnel , ndof ) ; kk=f e a s m b l 1 ( kk , k , i n d e x ) ; f f =f e a s m b l 1 f ( f f , f , i n d e x ) ; end Aplicación de las condiciones de contorno y comparación: 1 2 %CONDICIONES DE CONTORNO [ kk , f f ]= f e a p l y c 2 ( kk , f f , g d l b o r d e , v a l o r b o r d e , s d o f ) ; CAPÍTULO 8. ANEXO 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 98 %% R e s o l u c i o n d e l s i s t e m a s o l=kk\ f f ; x=x0 : ( x f i n −x0 ) / (Nx−1) : x f i n ; y=y0 : ( y f i n −y0 ) / (Ny−1) : y f i n ; c o n t =1; e s o l=z e r o s (Nx , Ny) ; f s o l=z e r o s (Nx , Ny) ; e r r o r _ r e l a t i v o=z e r o s (Nx , Ny) ; e r r o r _ a b s o l u t o=z e r o s (Nx , Ny) ; f o r i =1:Nx f o r j= 1 : Ny f s o l ( j , i )=s o l ( c o n t ) ; f s o l=f s o l ’ ; e s o l ( i , j )=a l f a ∗ c o s ( x ( i ) )+b e t a ∗ ( y ( j ) +4∗x ( i ) ) ^ 2 ; c o n t=c o n t +1; end end 20 21 22 23 24 %% En v a l o r a b s o l u t o e r r o r _ a b s o l u t o=abs ( e s o l −f s o l ) ; %% En v a l o r a b s o l u t o e r r o r _ r e l a t i v o=abs ( ( e s o l −f s o l ) ) . / ( e s o l+e p s ) ; 25 26 27 28 29 %% Máximo d e l e r r o r a b s o l u t o Error_maximo_absoluto=max(max( e r r o r _ a b s o l u t o ) ) ; %% Máximo d e l e r r o r r e l a t i v o Error_maximo_relativo=max(max( e r r o r _ r e l a t i v o ) ) ; Las siguientes funciones han sido sacadas de [4, capítulos 2 a 6] : feglqd2. Obtiene los puntos y pesos de la cuadratura. feisoq4. Permite obtener las funciones de forma Hm y sus derivadas evaluadas en los puntos de cuadratura. fejacob2. Determina el jacobiano de la transformación. feeldof. Prepara los grados de libertad donde ha de ensamblarse la matriz k y el vector f elementales. feasmbl1. Permite montar la matriz del sistema kk a partir de las elementales k. feasmbl1f. Modificación que se ha hecho a la anterior para montar el vector f. feaplyc2. Aplica las condiciones de contorno. Índice de figuras 2.1. Aproximación de una función mediante MRP. . . . . . . . . . . . 2.2. Comparación Galerkin-Colocación por puntos. . . . . . . . . . . . 17 20 3.1. 3.2. 3.3. 3.4. 3.5. 3.6. 3.8. 3.7. 3.9. . . . . . . . . . 26 28 29 30 32 33 34 34 36 4.1. Esquema del sistema péndulo invertido. . . . . . . . . . . . . . . 4.2. Solución Exacta de la ecuación diferencial. . . . . . . . . . . . . . 4.3. Recinto de integración para el MRP. . . . . . . . . . . . . . . . . 42 45 46 5.1. 5.2. 5.3. 5.4. 5.5. 5.6. 5.7. 5.8. 51 54 55 55 56 57 57 Dominio Ω al aplicar el MEF. . . . . . . . . . . . . . . . Dominio unidimensional. . . . . . . . . . . . . . . . . . . Elemento triangular. 3 Nodos. . . . . . . . . . . . . . . . Elemento rectangular. 4 Nodos. . . . . . . . . . . . . . . Elemento unidimensional isoparamétrico. . . . . . . . . Elemento triangular en coordenadas naturales. 3 Nodos. Cuadrilátero en coordenadas físicas. . . . . . . . . . . . Cuadrilátero en coordenadas naturales. . . . . . . . . . . Dominio unidimensional. 5 Elementos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Recinto de integración: primer cuadrante. . . . . . . . . . . . . . Solución aproximada MRP. Suma de potencias de polinomios. . . Error relativo MRP. Suma de potencias de polinomios. . . . . . . Error absoluto MRP. Suma de potencias de polinomios. . . . . . Solución aproximada MRP. Funciones sinusoidales. . . . . . . . . Error Relativo MRP. Funciones sinusoidales. . . . . . . . . . . . . Error absoluto MRP. Funciones sinusoidales. . . . . . . . . . . . Solución aproximada MRP. Cumpliendo también condiciones de contorno originales. M=4. . . . . . . . . . . . . . . . . . . . . . . 5.9. Error Relativo MRP. Cumpliendo también condiciones de contorno originales. M=4. . . . . . . . . . . . . . . . . . . . . . . . . 5.10. Error absoluto MRP. Cumpliendo también condiciones de contorno originales. M=4. . . . . . . . . . . . . . . . . . . . . . . . . 5.11. Solución aproximada MRP. Cumpliendo también condiciones de contorno originales. M=5. . . . . . . . . . . . . . . . . . . . . . . 5.12. Error Relativo MRP. Cumpliendo también condiciones de contorno originales. M=5. . . . . . . . . . . . . . . . . . . . . . . . . 99 58 59 59 60 60 ÍNDICE DE FIGURAS 100 5.13. Error absoluto MRP. Cumpliendo también condiciones de contorno originales. M=5. . . . . . . . . . . . . . . . . . . . . . . . . 5.14. Solución aproximada MRP. Cumpliendo también condiciones de contorno originales. M=6. . . . . . . . . . . . . . . . . . . . . . . 5.15. Error Relativo MRP. Cumpliendo también condiciones de contorno originales. M=6. . . . . . . . . . . . . . . . . . . . . . . . . 5.16. Error absoluto MRP. Cumpliendo también condiciones de contorno originales. M=6. . . . . . . . . . . . . . . . . . . . . . . . . 5.17. Distribución deltas. Caso 1. . . . . . . . . . . . . . . . . . . . . . 5.18. Distribución deltas. Caso 2. . . . . . . . . . . . . . . . . . . . . . 5.19. Error absoluto Dirac. M=4. Caso 1. . . . . . . . . . . . . . . . . 5.20. Error relativo Dirac. M=4. Caso 1. . . . . . . . . . . . . . . . . . 5.21. Error absoluto Dirac. M=4. Caso 2. . . . . . . . . . . . . . . . . 5.22. Error relativo Dirac. M=4. Caso 2. . . . . . . . . . . . . . . . . . 5.23. Distribución deltas M=5. Caso 1. . . . . . . . . . . . . . . . . . . 5.24. Distribución deltas M=5. Caso 2. . . . . . . . . . . . . . . . . . . 5.25. Error absoluto Dirac. M=5. Caso 1. . . . . . . . . . . . . . . . . 5.26. Error relativo Dirac. M=5. Caso 1. . . . . . . . . . . . . . . . . . 5.27. Error absoluto Dirac. M=5. Caso 2. . . . . . . . . . . . . . . . . 5.28. Error relativo Dirac. M=5. Caso 2. . . . . . . . . . . . . . . . . . 5.29. Error absoluto: Dirac con suma polinomios. . . . . . . . . . . . . 5.30. Error relativo: Dirac con suma polinomios. . . . . . . . . . . . . . 62 65 65 66 67 67 68 68 69 69 70 70 71 71 72 6.1. Mallado para MEF. . . . . . . . . . . . . . . . . . . . . . . . . . 6.2. Normal en los bordes (MEF). . . . . . . . . . . . . . . . . . . . . 75 80 61 61 62 Bibliografía [1] Lucas Rodríguez (2012). Resolución numérica de EDPS asociadas a problemas de control [2] Casanovas Espinar (2014). Aplicación del MDF y del MEF a problemas de control [3] Acosta Rodríguez, J.A.(2004). Control no lineal de sistemas subactuados. PhD tesis. Universidad de Sevilla. Sevilla. [4] Y. W. Kwon y H. C. Bang (1997). The Finite Element Method using Matlab [5] Flores F. y Brewer A. Introducción al Método de Elementos Finitos. Universidad de Córdoba. Argentina. [6] Domínguez Abascal, J. Teoría de estructuras. Universidad de Sevilla. Sevilla. 101