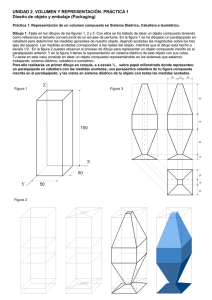
Perspectivas. Caballera

Perspectivas. Caballera
En este nuevo tema ampliaremos los conceptos y procedimientos sobre la perspectiva caballera, aprendidos en el
curso pasado. No obstante, te recomendamos que repases los contenidos desarrollados en el tema 3
(axonometría oblicua: caballera) de la Unidad Didáctica IV, los sistemas de representación.
Aprenderás a proyectar las superficies poliédricas y radiadas en posiciones más complejas respecto de los ejes de
coordenadas axonométricos. Y a determinar la intersección de un plano sobre dichas superficies.
En la imagen superior puedes ver un "trampantojo" realizado en una de las capillas de la catedral de Santa de
Cecilia en Albi (Francia), observa cómo la ubicación de cada perspectiva del prisma rectangular concede a la
composición una mayor profundidad.
Actividad
1 de 45
Archivo no
encontrado
Firefox no puede
encontrar el archivo
en /embed
/9Dd8DhpyZmI.
Antes de empezar te aconsejamos que visualices el vídeo superior, en él puedes ver cómo traza
la perspectiva caballera de una figura.
2 de 45
1. Generalidades
A diferencia de la axonometría ortogonal (isometría) en la perspectiva caballera es aconsejable aplicar siempre el
coeficiente de reducción. Recordarás que este lo hacíamos de dos maneras sobre cada magnitud del dibujo
relacionada con el eje Y (profundidades):
Matemáticamente: aplicamos el coeficiente (1/2 = 0,5)
Gráficamente: construimos el vector dirección de reducción según el coeficiente dado, y mediante
paralelas lo aplicamos.
Como ya hemos hecho en la perspectiva isométrica, en este tema también aplicaremos un método ya aprendido
en el sistema diédrico: el abatimiento; pero solamente los planos XOY e YOZ, ya que el XOZ está en verdadera
magnitud.
Además aprenderás a determinar la intersección entre recta y plano, y entre planos.
Antes de empezar te aconsejamos que repases los contenidos y procedimientos del curso anterior explicados en
el tema 3. Axonometría Oblicua: Caballera, de la unidad didáctica IV, los sistemas de representación (II).
En la imagen superior puedes ver algunas varias figuras planas representadas en perspectiva caballera, según un
determinado coeficiente de reducción.
Conocimiento previo
3 de 45
Perspectiva caballera y Arte.
Mediante esta aplicación alojada en la web oficial de la Galería Nacional de Arte (NGA) de la
ciudad de Washington (USA) podemos diseñar figuras geométricas quitando cubos (hexaedros)
visualizándolas además desde distintos puntos de vista.
Pulsa sobre la imagen para acceder a la web.
Pregunta Verdadero-Falso
4 de 45
Según lo explicado en el curso anterior determina si las siguientes afirmaciones sobre el
coeficiente de reducción son ciertas:
Es la relación entre la proyección de un segmento del eje X, y su longitud real en el
espacio.
Verdadero Falso Es la relación entre la proyección de un segmento del eje Y, y su longitud real en el
espacio.
Verdadero Falso Es la relación entre la proyección de un segmento del eje Z, y su longitud real en el
espacio.
Verdadero 5 de 45
Falso 1.1. Coeficiente de Reducción
Actividad
Podemos determinar el coeficiente de reducción usando cualquier eje (X o Z); pero por comodidad
usaremos la prolongación del eje Z (-Z).
6 de 45
Coeficiente de reducción 2/3.
En la siguiente animación puedes ver cómo hemos determinado la perspectiva caballera de un triángulo ABC,
según los siguientes datos:
Lado AC paralelo a un eje axonométrico (X).
Ángulo XOY = 135º (perfil derecho).
CR = 2/3.
7 de 45
Coeficiente de reducción 1/2.
En la siguiente animación te mostramos cómo hemos determinado la perspectiva caballera de un cuadrado ABCD,
según los siguientes datos:
Lados oblicuos a los ejes axonométricos.
Ángulo XOY = 45º (perfil izquierdo).
CR = 1/2.
Objetivos
8 de 45
Mediante el siguiente vídeo puedes repasar cómo se determina gráficamente el vector dirección
que representa al coeficiente de reducción. Archivo no
encontrado
Firefox no puede
encontrar el archivo
en /embed
/T06czN5lqM4.
9 de 45
1.2. Intersecciones
Para determinar la perspectiva caballera de la intersección entre dos planos, o entre una recta y un plano debemos
representar sus proyecciones axonométricas, aplicando el coeficiente de reducción mediante abatimiento.
Se entiende que la recta o el punto intersección es la proyección directa.
En la imagen superior puedes ver cómo se ha determinado la intersección entre dos planos paralelos a la línea de
tierra, lógicamente la recta solución será una recta paralela a dicha línea.
10 de 45
Intersección entre planos.
La intersección de las trazas de los planos nos determinará la proyección directa de la recta intersección.
En la siguiente animación te mostramos cómo se determina la recta intersección entre dos planos paralelos a la
LT.
11 de 45
Intersección entre recta y plano.
La proyección directa del punto intersección quedará determinada por la intersección entre una de las trazas del
plano y la proyección secundaria correspondiente de la recta.
En la animación inferior te mostramos cómo se ha determinado la intersección de una recta de perfil con un plano
paralelo a la LT. En este caso la intersección de la traza del plano con la proyección secundaria (perfil) nos
determina la proyección directa del punto intersección.
12 de 45
1.3. Circunferencia por afinidad
Dependiendo de cómo esté dispuesta la circunferencia respecto de los planos del triedro, obtendremos dos tipos
de proyecciones:
Circunferencia: si la curva está contenida o es paralela al plano XOZ.
Elipse: si la curva contenida o es paralela a los planos XOY, YOZ.
Así pues para este último caso, podemos aplicar los conceptos y procedimientos aprendidos en los temas de la
Unidad Didáctica II: Curvas y transformaciones proyectivas de Dibujo Técnico II, para representar la perspectiva
caballera de la circunferencia.
En la imagen superior puedes ver cómo se ha obtenido la perspectiva caballera de la circunferencia, contenida en
el plano XOY, aplicando dos métodos (abatimiento y afinidad).
La elipse proyección se ha obtenido determinado sus diámetros conjugados (abatimiento) y en los ejes (afinidad).
Para simplificar su trazado la hemos inscrito en un cuadrado.
Actividad
13 de 45
Recuerda que las diagonales de un cuadrado que circunscribe a una circunferencia, determina en
esta unos puntos específicos.
En el siguiente vídeo puedes ver la relación que se establece entre dichos puntos y las distintas
perspectivas de la circunferencia.
Archivo no
encontrado
Firefox no puede
encontrar el archivo
en /embed
/DJOQJtVS_ns.
14 de 45
Métodos.
En el tema 1, curvas cónicas (I), de la Unidad Didáctica II: Curvas y Transformaciones Proyectivas, vimos varios
métodos que nos permitían representar la perspectiva isométrica y caballera de una circunferencia, obteniendo
siempre la posición exacta de los ejes de simetría de la elipse, pero no su magnitud; pero en cambio, sí podíamos
situar dos de sus diámetros conjugados y las longitudes de ambos.
En este tema vamos a estudiar de manera detenida dichos métodos, lo que nos permitirá determinar de manera
rápida y sencilla los puntos de la elipse, perspectiva caballera de la circunferencia.
Por puntos. Método general similar al usado en isométrico, establecemos una afinidad entre los puntos de
la circunferencia del plano ZOX y la elipse del YOX.
Por abatimiento. Abatimos el plano YOX sobre el plano del cuadro ZOX, u otro plano paralelo a este.
También se establece una relación de afinidad.
Por Afinidad. La circunferencia del plano ZOX y la elipse del YOX son afines, siendo el eje X el eje de
afinidad, la dirección de afinidad queda determinada por el segmento que uno los centros de las curvas.
En la animación inferior puede ver de manera detallada el procedimiento que debes seguir para obtener la
perspectiva caballera, mediante afinidad, de una circunferencia contenida en el plano XOY.
15 de 45
Objetivos
El trazado de la perspectiva caballera de la circunferencia es parte esencial en la construcción de
superficies radiadas como el cono y el cilindro.
En el siguiente vídeo puedes ver cómo a partir de la perspectiva caballera de la circunferencia
base de un cilindro recto de revolución se obtiene la perspectiva de dicha superficie.
Archivo no encontrado
Firefox no puede encontrar el
archivo en /embed/pT95aD5D5Rk.
Compruebe que el nombre de
archivo no tiene errores de
escritura, incluyendo el uso de
mayúsculas.
Compruebe si el archivo ha sido
movido, renombrado o eliminado.
16 de 45
Caso de estudio
En la imagen superior
puedes ver cómo se ha
trazado la perspectiva
caballera de una
circunferencia contenida en
el plano XOY, según los
parámetros establecidos.
Dicha circunferencia es
tangente a los plano XOZ
e YOZ, por tanto será
también tangente a los ejes
axonométricos X e Y.
Te pedimos que apliques
los contenidos y
procedimientos adquiridos
hasta ahora para trazar la
perspectiva caballera
mediante las herramientas
de dibujo tradicionales.
Para realizar este ejercicio debes descargar este documento pdf. 17 de 45
2. Poliedros
Como hicimos en el tema anterior, perspectiva isométrica, también vamos a estudiar solamente los siguientes
poliedros: tetraedro, hexaedro y octaedro.
En la imagen superior puedes ver la perspectiva caballera de estos poliedros.
Actividad
Para representar cualquier poliedro primero debemos representar su proyección sobre el plano en
el que está apoyado y finalmente levantaremos sus alturas.
18 de 45
2.1. Tetraedro
La perspectiva caballera del tetraedro no presenta dificultad alguna, salvo la determinación de su altura.
Podemos aplicar lo aprendido en su representación para obtener la perspectiva caballera de las pirámides
regulares.
En la imagen superior puedes ver cómo se ha determinado la perspectiva caballera de un tetraedro cuyas aristas
básicas son oblicuas a los ejes de coordenadas axonométricos.
Actividad
Recuerda que para obtener las proyecciones diédricas de un tetraedro solamente necesitamos
conocer la longitud de su arista, ya que altura la podemos determinar mediante el abatimiento de
su sección principal.
19 de 45
Arista base paralela a un eje axonométrico.
En este caso una de las aristas base está contenida en uno de los ejes de coordenadas axonométrico.
En la siguiente animación puedes ver cómo se ha trazado la perspectiva caballera de dicho poliedro según un
coeficiente de reducción dado.
20 de 45
Aristas bases oblicuas a los ejes axonométricos.
En este caso particular hemos dispuesto una de las aristas base con un ángulo de 15º grados respecto del eje de
coordenadas axonométrico X.
En la animación inferior te mostramos cómo se determina la perspectiva de dicho poliedro.
Caso práctico
21 de 45
En la imagen superior puedes ver cómo se ha trazado la perspectiva caballera de un tetraedro apoyado por su cara
ABC en el triedro XOY, según los parámetros establecidos.
Conocemos las proyecciones diédricas del poliedro.
Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para trazar la perspectiva caballera
mediante las herramientas de dibujo tradicionales.
Para realizar este ejercicio debes descargar este documento pdf. 22 de 45
2.2. Hexaedro
Como ya vimos en el tema anterior la representación de la perspectiva del Hexaedro es la más sencilla de
representar ya que su altura se corresponde con la longitud de su arista.
Podemos aplicar lo aprendido en su representación para obtener la perspectiva caballera de los prismas regulares.
En la imagen superior te mostramos cómo se ha determinado la perspectiva caballera de un hexaedro cuyas
aristas básicas son oblicuas a los ejes de coordenadas axonométricos.
23 de 45
Arista base paralela a un eje axonométrico.
Como la base es un cuadrado si una arista base es paralela a uno de los ejes de coordenadas axonométricos, las
otras lo serán al otro correspondiente.
En este caso particular la arista está contenida en el eje X.
En la animación inferior te mostramos el procedimiento a seguir para trazar la perspectiva de dicho poliedro.
24 de 45
Aristas bases oblicuas a los ejes axonométricos.
En este caso particular hemos dispuesto una de las aristas base con un ángulo de 30º grados respecto del eje de
coordenadas axonométrico X.
En la animación inferior te mostramos cómo se determina la perspectiva de dicho poliedro.
Objetivos
25 de 45
En el siguiente vídeo puedes ver cómo, a partir de la construcción de varios hexaedros, podemos
obtener la perspectiva caballera de formas más complejas.
Archivo no
encontrado
Firefox no puede encontrar
el archivo en /embed
/WtpVv2YNMy8.
Caso práctico
26 de 45
En la imagen superior te mostramos cómo se ha trazado la perspectiva caballera de un hexaedro ABCDEFGH
apoyado sobre el triedro XOY por una de sus caras (ABCD), siendo las secciones principales perpendicular y paralela
al plano XOZ.
Conocemos las proyecciones diédricas de dicho poliedro.
Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para su resolución mediante las
herramientas de dibujo tradicionales.
Para realizar este ejercicio debes descargar este documento pdf. 27 de 45
2.3. Octaedro
Como ya vimos en el tema anterior, dada la complejidad de este poliedro solamente vamos a determinar la
perspectiva caballera a partir de una posición particular: apoyado en el plano YOX por un vértice de la arista
principal, perpendicular a dicho plano.
Recuerda que cuando un octaedro está apoyado en el plano de proyección por una de sus diagonales principales,
perpendicular a dicho plano, cuatro de sus aristas tienen la misma cota, por lo que estarán contenidas en un plano
horizontal.
En la imagen superior puedes ver cómo hemos determinado la perspectiva caballera de un octaedro siendo sus
aristas horizontales oblicuas a los ejes de coordenadas axonométricos.
Actividad
Recuerda que para poder representar la perspectiva de un octaedro necesitamos conocer, como
mínimo, la medida de su arista, ya que su altura vendrá dada por su diagonal principal.
28 de 45
Aristas horizontales paralelas y perpendiculares a los ejes axonométricos.
En este caso dos de las aristas horizontales están en planos del triedro (XOZ e YOZ).
En la siguiente animación te mostramos el procedimiento a seguir.
29 de 45
Aristas horizontales oblicuas a los ejes axonométricos.
En este caso particular hemos dispuesto una de las aristas horizontales con un ángulo de 30º grados respecto del
eje de coordenadas axonométrico X.
En la animación inferior te mostramos cómo se determina, mediante abatimiento de la planta sobre el plano XOZ,
la perspectiva de dicho poliedro.
Caso de estudio
30 de 45
En la imagen superior te mostramos cómo se ha trazado la perspectiva caballera de un octaedro ABCDEF apoyado
sobre el triedro XOY por una de sus diagonales principales (AF), siendo una de las diagonales principales una recta
paralela a la LT.
Conocemos las proyecciones diédricas de dicho poliedro.
Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para su resolución mediante las
herramientas de dibujo tradicionales.
Para realizar este ejercicio debes descargar este documento pdf. 31 de 45
3. Superficies radiadas
La realización de la perspectiva caballera de las superficies radiadas nos permitirá acometer el trazado de figuras
más complejas.
En la imagen superior te mostramos la perspectiva caballera de un prisma y una pirámide regulares; y de un
cilindro y un cono rectos de revolución.
32 de 45
3.1. Pirámides
Como vimos en el tema anterior, el trazado de su perspectiva es similar al del Tetraedro, salvo por la
determinación de su altura que siempre nos vendrá dada.
Dado que la base de estas superficies debe ser un polígono regular (triángulo equilátero, cuadrado, pentágono,
hexágono, etc..) la resolución de cualquier perspectiva caballera debe pasar primero por la de dicha figura plana.
Así pues, siempre comenzaremos dibujando la perspectiva de la planta y luego determinaremos el vértice de la
altura.
En la imagen superior te mostramos la perspectiva de una pirámide regular de base cuadrangular, según sus
vistas diédricas dadas.
Actividad
Vuelve a repasar los conceptos y procedimientos sobre polígonos regulares.
33 de 45
Aristas bases oblicuas a los ejes axonométricos (base triangular).
Como la pirámide es regular la base debe ser un triángulo equilátero, por lo que tendrá cierta similitud con el
trazado del Tetraedro.
En este caso particular uno de los vértices está contenido el centro O del triedro.
En la animación inferior te mostramos el procedimiento a seguir para trazar la perspectiva caballera de dicha
pirámide.
34 de 45
Aristas bases oblicuas a los ejes axonométricos (base cuadrangular).
En este caso particular hemos dispuesto una de las aristas base con un ángulo de 30º grados respecto del eje de
coordenadas axonométrico X.
En la animación inferior te mostramos cómo se determina, mediante abatimiento de la planta sobre el plano XOZ,
la perspectiva de dicho poliedro.
Caso de estudio
35 de 45
En la imagen superior te mostramos cómo se ha trazado la perspectiva caballera de una pirámide regular ABCDEFG
de base hexagonal apoyada en el triedro XOY por su base ABCDEF.
Conocemos sus proyecciones diédricas, siendo sus aristas bases oblicuas a los ejes axonométricos.
Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para su resolución mediante las
herramientas de dibujo tradicionales.
Para realizar este ejercicio debes descargar este documento pdf.
36 de 45
3.2. Prismas
La determinación de su perspectiva es similar al del Hexaedro, excepto por la altura que siempre nos vendrá dada.
Como la base de estas superficies debe ser un polígono regular (triángulo equilátero, cuadrado, pentágono,
hexágono, etc..) la resolución de cualquier perspectiva caballera debe pasar primero por la de dicha figura plana.
Por tanto, debemos comenzar trazando la perspectiva de la planta, aplicando el coeficiente de reducción dado, y
finalmente dibujar las aristas laterales.
En la imagen superior puedes ver la perspectiva de un prisma regular de base triangular, dibujada según sus vistas
diédricas dadas.
Actividad
Nosotros solamente vamos a estudiar los cilindros rectos de revolución y los prismas regulares.
37 de 45
Arista base paralela a un eje axonométrico.
Como las bases del prisma son pentágonos regulares solamente puede tener una arista paralela a uno de los ejes
de coordenadas axonométrico.
En este caso particular la arista está contenida en el eje X.
En la animación inferior te mostramos el procedimiento a seguir para trazar la perspectiva caballera de dicho
prisma.
38 de 45
Aristas bases oblicuas a los ejes axonométricos.
En este caso particular hemos dispuesto una de las aristas bases con un ángulo de 30º respecto del eje de
coordenadas axonométrico X, además un vértice de la base está contenido en el centro O del triedro.
En la animación inferior puedes ver cómo se ha determinado la perspectiva de dicho prisma.
Caso práctico
39 de 45
En la imagen superior te mostramos cómo se trazado la perspectiva caballera de un prisma regular ABCDEFGIJKLM
de base hexagonal apoyado el triedro XOY.
Conocemos sus proyecciones diédricas, siendo sus aristas bases oblicuas a los ejes axonométricos.
Te pedimos que apliques los contenidos y procedimientos adquiridos hasta ahora para su resolución mediante las
herramientas de dibujo tradicionales.
Para realizar este ejercicio debes descargar este documento pdf. 40 de 45
4. QCAD. Ejercicios
En esta unidad didáctica continuamos aplicando los conceptos y procedimientos aprendidos sobre el manejo de la
aplicación QCAD para resolver ejercicios, en este caso el trazado de perspectivas caballeras de superficies
poliédricas y radiadas.
Debes crear en cada archivos dxf una capa llamada trazado para realizar en ella los trazados.
Recuerda que no pretendemos que aprendas nuevas herramientas o comandos, solamente te pedimos que
repases las prácticas que has realizado hasta ahora.
41 de 45
4.1. Poliedros
Aplicando los conceptos y procedimientos aprendidos sobre el programa QCAD realiza los siguientes ejercicios:
Caso de estudio
En la imagen superior puedes ver cómo se ha trazado la perspectiva caballera de un tetraedro seccionado por un
plano P paralelo a la LT (paralelo al eje X).
Para su dibujo conocemos las proyecciones del poliedro y de las trazas del plano secante P.
Te pedimos que, mediante las herramientas de la aplicación QCAD, determines la perspectiva caballera del tetraedro
seccionado, según los parámetros establecidos.
Para realizar este ejercicio debes descargar este archivo dxf. Caso práctico
42 de 45
En la imagen superior te mostramos cómo hemos determinado la perspectiva caballera de un hexaedro seccionado
por un plano P proyectante vertical (de canto).
Para su dibujo conocemos las proyecciones del poliedro y las trazas del plano P.
Te pedimos que, mediante las herramientas de la aplicación QCAD, determines la perspectiva del hexaedro
seccionado, según los parámetros establecidos.
Para realizar este ejercicio debes descargar este archivo dxf. 43 de 45
4.2. Superficies radiadas
Aplicando los conceptos y procedimientos aprendidos sobre el programa QCAD realiza los siguientes ejercicios:
Caso práctico
En la imagen superior puedes ver cómo se ha trazado la perspectiva caballera de una pirámide regular de base
pentagonal seccionada por un plano P proyectante vertical (plano de canto).
Para su dibujo conocemos las proyecciones de la pirámide y la perspectiva caballera del plano secante P.
Te pedimos que, mediante las herramientas de la aplicación QCAD, determines la perspectiva caballera de la
pirámide seccionada, según los parámetros establecidos.
Para realizar este ejercicio debes descargar este archivo dxf. Caso práctico
44 de 45
En la imagen superior te mostramos cómo se ha trazado la perspectiva caballera de un prisma regular de base
hexagonal seccionado por un plano P plano paralelo a la LT (eje isométrico X).
Para su dibujo conocemos las proyecciones del prisma y de las trazas del plano P.
Te pedimos que, mediante las herramientas de la aplicación QCAD, determines la perspectiva caballera del prisma
seccionado, según los parámetros establecidos.
Para realizar este ejercicio debes descargar este archivo dxf. 45 de 45