Movimiento Amortiguado
Anuncio
Movimiento Amortiguado
Se ha discutido en la primera parte del curso, los conceptos relacionados con el movimiento oscilatorio,
con énfasis general, en el movimiento oscilatorio armónico. No hay que olvidar, como se advirtió
oportunamente, que el movimiento armónico simple, es la primera aproximación en el estudio de ésta
clase de movimientos. Ahora tenemos que enfrentar la realidad. Si bien estos movimientos constituyen
la fuente de la propagación ondulatoria de la energía, el hecho de restringir el estudio a los
movimientos armónicos, es sólo por simplicidad, porque aún los movimientos anarmónicos, siguen
siendo fuentes de la misma propagación ondulatoria de la energía, solo que en esos casos, serían ondas
anarmónicas. No hay que olvidar, que aún las representación ondulatoria más compleja, siempre puede
ser descompuesta (análisis de Fourier) en ondas armónicas simples.
Para tratar de visualizar de alguna forma la diferencia entre los sistemas; sin y con, amortiguamiento,
es necesario analizar con cuidado las oscilaciones en general.
Estudiante. ¿Qué es lo que llamamos amortiguamiento?
Profesor. Buena y oportuna pregunta; seguramente por lo acostumbrados que estamos con él, no nos
hemos detenido a analizarlo. Usted en el curso de mecánica debe haber aprendido algo que llamamos
fricción.
(a)
(b)
(c)
d)
Figura 1
Estudiante. Si, aprendí que es una fuerza que aparece entre la superficie de los cuerpos en
movimiento relativo, que es una de las fuerzas que aparecen en los sistemas en movimiento, y que está
dirigida en dirección opuesta a la del movimiento. Además, en la mayoría de los casos, se ignora. Pero
¿qué tiene que ver la fricción con el amortiguamiento, en los sistemas oscilatorios?
Profesor. Tratemos de ilustrar la situación de la siguiente forma:
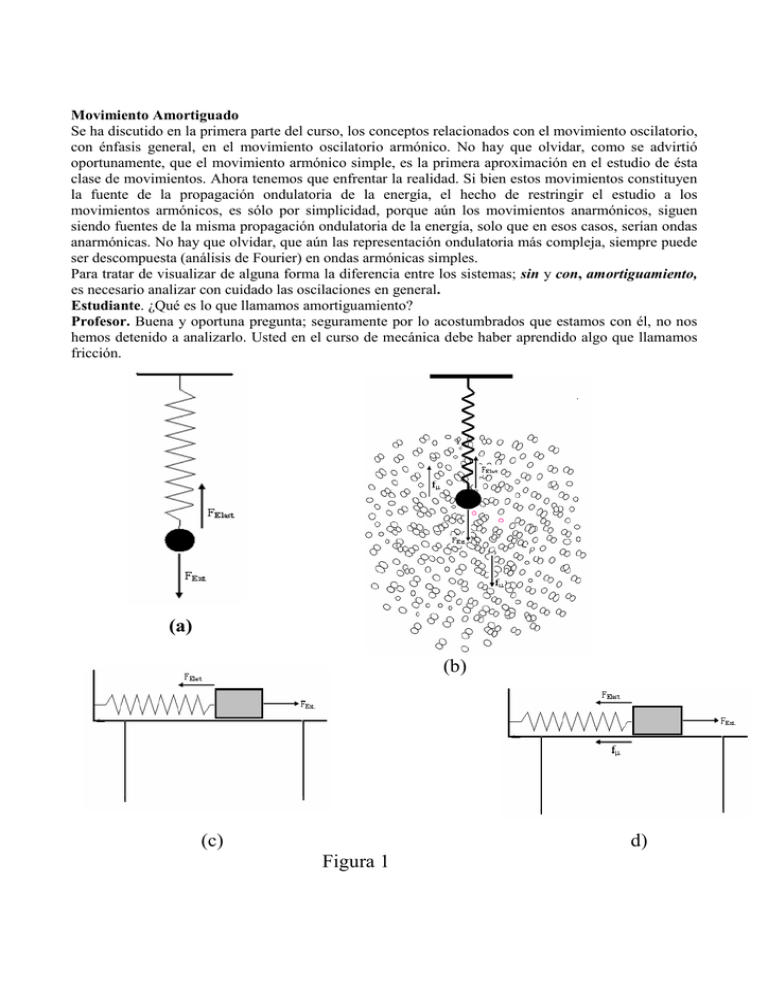
En la fig. 1, involucramos el sistema masa resorte, por considerarlo el más ilustrativo para esta clase de
discusiones. En todos los gráficos mostrados: (a), (b), (c) y (d), incluyo una fuerza externa, FExt., ya que
nuestro interés está centrado en el fenómeno de propagación de la energía; así que, ésta fuerza será la
que hace el trabajo de perturbar los sistemas, inicialmente en equilibrio. También se incluyen: las
fuerza elástica, FElast., que es la respuesta del sistema a la fuerza externa; y la fuerza de fricción o
resistente, fµ, que está asociada con la interacción entre el sistema y su entorno.
Profesor. ¿Hay algo que le llame la atención en la fig. 1?
Estudiante. Sí, varias cosas. En las figs (a) y (c), no hay fuerza de fricción, ¿por qué?, y en las figs. (b)
y (d), si hay fuerza de fricción, además ¿por qué en (b) hay dos fuerzas de fricción?
Profesor. Parece que está muy atento, eso esta muy bien. Evidentemente, en las figs (a) y (c), estoy
incluyendo la situación del movimiento oscilatorio armónico, tratado en la primera parte (el tema
anterior), o sea, el caso ideal (no real). En las figs (b) y (d), la fuerza de fricción está justificando la
presencia del entorno del sistema, con el cual interactúa éste cuando está en movimiento. Las fuerzas
de fricción en la fig. (b), está representando la resistencia que ofrece el medio, al sistema en
movimiento, cuando va hacia abajo, y cuando va hacia arriba, en la dirección del movimiento.
Estudiante. Por lo que se indica en la fig. (d), entiendo que la dirección de la fuerza de fricción, esta
dirigida hacia la izquierda, debido a que la fuerza externa desplaza la masa hacia la derecha; pero
cuando la masa se desplaza en sentido contrario, por la acción de la fuerza elástica; esa misma fuerza
de fricción, estará dirigida hacia la derecha, pues por lo que aprendí en el curso de mecánica, la fuerza
de fricción siempre esta dirigida en dirección opuesta a la del movimiento.
Profesor. Eso es correcto.
Estudiante. Hay algo que me llama la atención, en relación con las figs. (b) y (d). En la fig. (b), las
fuerzas de fricción justifican la interacción del sistema con el entorno, pero en la fig. (d), sólo se hace
referencia a la fricción entre las superficies de la mesa y la masa, ¿es que el entorno no actúa como lo
hace en la fig. (b)?
Profesor. Esa inquietud me parece muy pertinente. Efectivamente, en éste caso, no es que el entorno
no actúe sobre el sistema como en la fig. (b), lo que ocurre es que, en una primera aproximación,
comparando el efecto de la fricción entre las superficies, con la fricción de la masa con el entorno (por
ej. el aire), en términos de disipación de energía, el primero es mucho mayor que el segundo; por eso
despreciamos el segundo. Pero en una descripción más rigurosa, evidentemente hay que tener en cuenta
esa interacción.
Estudiante. Pero para plantear la ecuación de movimiento del sistema, ¿cómo se puede definir esa
fuerza de fricción?
Profesor. Esa es una cuestión difícil de responder en términos simples. Como usted pudo apreciar en el
caso de la fricción entre cuerpos sólidos, la relación entre la fuerza de fricción y el peso del cuerpo, es
una constante de proporcionalidad. Recuerde que si está analizando el sistema estático, antes de iniciar
el movimiento, entre las fuerzas, externa y de reacción, media el coeficiente de fricción estático, µs; y si
analiza el sistema, en movimiento, el coeficiente es, µd. Estos coeficientes: µs y µd, involucran las
características de las superficies interactuantes, en reposo y en movimiento. En nuestro caso,
hablaremos, o tendremos en cuenta sólo, la parte dinámica; y para tener una idea sobre una de las
características más importantes, consideremos la siguiente situación. Un sistema oscilatorio, el sistema
masa-resorte, en un líquido de densidad, ρL, y el mismo sistema en un gas (puede ser el aire) de
densidad, ρg, y en el vacío. Si perturbamos con una misma fuerza externa (la misma energía), el
sistema en los tres casos, ¿cómo serán los tiempos que cada sistema permanezca oscilando? Ver la
figura 2.
ρg
(a)
(b)
(c)
Figura 2
Estudiante. En la primera parte del curso vimos, que al no tener el sistema a quien transferir la energía
con la que fue perturbado, tendría que oscilar indefinidamente (caso ideal), eso equivale al caso (a). En
el segundo caso; en el medio gaseoso, el sistema va a encontrar a quien entregarle la energía, y lo hace
a través del movimiento oscilatorio, de suerte que, el sistema tendrá un tiempo determinado (finito)
para disipar la energía con que fue perturbado, después del cual se detendrá. Lo mismo sucederá en el
caso se encontrarse en un líquido. Si tenemos en cuenta la densidad de los medios, lo que se puede
apreciar es que: en principio, en el primer caso el tiempo de oscilación es infinito; en el segundo, es
finito; y en el tercero, también es finito, pero menor que en el segundo.
Profesor. Entre el segundo y el tercer caso, ¿a qué le puede atribuir usted esa diferencia de tiempo?
Estudiante. Debe ser porque, cuando la masa se mueve, ella encuentra más partículas por unidad de
tiempo en el caso del líquido, comparada con las que encuentra en el gas, y entonces tiene más o menos
partículas a quien transferirles la energía, disipándola más rápido en el líquido.
Profesor. Muy bien, veo que está asociando correctamente los principios discutidos hasta hora. Según
ese punto de vista, ¿cree usted que si la densidad del medio aumenta, disminuirá el tiempo de
oscilación?
Estudiante. Efectivamente, debe haber alguna relación entre ellos, donde la densidad juega un papel
muy importante.
Profesor. Correcto; lo que ocurre es que establecer algún tipo de relación, en esos términos, puede ser
complicado, a este nivel de discusión; pues eso puede implicar el tener que detallar rigurosamente la
estructura interna del medio, lo que no es una tarea fácil.
Estudiante. Entonces, ¿como podemos darle una forma matemática más simple a la fuerza de fricción?
Profesor. Si usted pudo relacionar el tiempo total de oscilación con la densidad del medio, ¿qué
opinión le merece la siguiente situación: usted hablo de un tiempo total finito de oscilación de cada
sistema, para disipar la energía de perturbación, ¿qué puede decir sobre el número promedio de
partículas que la masa encuentra en su camino por unidad de tiempo, en cada uno de los dos últimos
sistemas?
Estudiante. Me parece que la respuesta es la misma, en el de mayor densidad, encuentre más
partículas.
Profesor. Efectivamente, miren que son dos formas de hacer la misma pregunta. También tenga en
cuenta que, en la medida que usted entienda muy bien las cosas, como ha ocurrido con usted en ésta
discusión, no importa como le pregunten, puede responder de manera coherente. Cuando uno no
entiende bien las cosas, por muy clara que sea la manera de preguntar, no hay esa coherencia.
Profesor. Con la intensión de llegar a aquella expresión simple para la fuerza de fricción, también
llamada, fuerza resistiva, le planteo la situación de otra manera, involucrando la velocidad con que
oscila la masa del sistema. En un tiempo determinado, t (puede ser un segundo), un sistema puede
oscilar con diferente velocidad cada vez, ¿cuándo la masa del sistema en cuestión, encuentra más
partículas en su recorrido?
Estudiante. Pienso que, tratándose de un medio homogéneo, cuando se mueva con más velocidad.
Profesor. Muy bien, parece que ya está preparado para escribir la forma de esa fuerza. Como ya pudo
percibir, hay muchas cosas, de las cuales ella depende, y al pretender involucrarlas a todas en una
relación para la fuerza resistiva, no la podríamos escribir de manera sencilla, como es nuestra intensión.
Lo que si tenemos que tener muy presente es que los parámetros como: la densidad, temperatura,
presión, tamaño de las partículas, formas de interacción, etc, tienen de alguna manera, en mayor o
menor proporción, incidencia sobre esa fuerza. Igual que cuando escribimos la forma de la fuerza
elástica de un resorte, en primera aproximación, como FElact. = - kx; aquí, por lo que acabamos de decir,
esa fuerza resistiva debe ser linealmente proporcional a la velocidad, y la escribimos como, fr = fµ = bv; donde b es una constante (que cumple un papel análogo al de k), y tiene que ver con aquellos
parámetros que no están explícitos en la forma de la fuerza. Su carácter resistivo esta asociado con el
hecho, de que se opone al movimiento, u otra forma de decir, que absorbe la energía del sistema. Mire
como toda la discusión, quedo condensada en una expresión muy sencilla de manejar. Por eso insisto
tanto, en la necesidad de entender muy bien los conceptos, para poder ver todo lo que hay detrás de
esas formas matemáticas simples que llamamos fórmulas, en ellas, queda condensada toda la
información, y es por esa información por la que usted es citado a clase, talleres, y todas las formas de
aprendizaje que se implementan en los cursos.
Ahora escribamos la ecuación dinámica de esos sistemas, donde el sistema oscilatorio interactúa con
las partículas de su entorno, llamados a esos sistemas, amortiguados. La interacción es, entre partículas,
por consiguiente, la transferencia (disipación) de la energía que se realiza en el proceso, es energía
mecánica.
FExt. = - kx – bv = ma = md2x/dt2
d 2 x b dx k
Haciendo b/m = γ y k/m = ωo
+
+ x=0
dt 2 m dt m
Aquí, γ es el factor de amortiguamiento; γdx/dt es el término disipativo; y ωo es la frecuencia propia
del sistema, sin amortiguamiento.
d 2x
dx
+γ
+ ω o x = 0 , que a diferencia del
2
dt
dt
movimiento armónico simple (ecuación diferencial lineal incompleta), ahora es una ecuación
diferencial completa.
La ecuación del movimiento amortiguado es entonces;
No obstante, que éste tipo de ecuaciones, tienen varias formas de solución, el que parece ser más
apropiado a nuestros intereses, tiene que ver con el uso del método que usa una ecuación característica
(método de exponenciales), que reduce la ecuación diferencial a una ecuación cuadrática, en términos
de la variable que redesigna los operadores diferenciales por λ2 y λ respectivamente, y las constantes γ
y ωo; así que la ecuación diferencial se convierte en
λ2 + γλ + ω o = 0
⇒ λ1,2 = [-γ ± (γ2 - 4ωo2)1/2]/2 = - γ/2 ±(γ2/4 - ωo2)1/2
y podemos escribir la solución general de la ecuación diferencial como
x(t ) = Ae λ1t + Be λ2t con λ1 = - γ/2 + (γ2/4 - ωo2)1/2 y λ2 = - γ/2 - (γ2/4 - ωo2)1/2
o sea, x(t) = A Exp.( - γ/2 + (γ2/4 - ωo2)1/2)1/2t + B Exp.( - γ/2 - (γ2/4 - ωo2)1/2t
x(t) = e-γt/2 [A Exp.(γ2/4 - ωo2)1/2t + B Exp.- (γ2/4 - ωo2)1/2t]
Normalmente en los cursos de ecuaciones diferenciales, los matemáticos utilizan el movimiento
amortiguado, como una aplicación física de esa importante herramienta matemática. En ese caso, del
análisis del radical, (γ2/4 - ωo2)1/2, surgen tres posibles soluciones para el sistema:
a) cuando (γ2/4 > ωo2), el radical es positivo, y las exponenciales son reales, crecientes y
decrecientes, no es un sistema oscilatorio (sobre amortiguado); por lo que en nuestra discusión,
no es de interés.
b) Cuando (γ2/4 = ωo2), aquí el factor dominante es el prefactor de amortiguamiento, que es una
exponencial decreciente, y el sistema se extingue en función de γ (amortiguamiento crítico). De
ese modo, el estado de oscilación dependerá de la magnitud de γ.
En tales circunstancias, los sistemas podemos decir que se transfieren la energía, si se quiere, hasta
abruptamente; y en tal circunstancia, pueden volverse muy atractivos, por la magnitud de sus
consecuencias.
c) cuando (γ2/4 < ωo2), en este caso, la solución tiene un comportamiento oscilatorio, que lo podemos
hacer muy importante, dependiendo de cómo sea la magnitud de la diferencia, (ωo2 - γ2/4). La fig. 3,
muestra tres casos típicos: a) cuando γ = 0 (caso ideal, movimiento armónico); b) con un
amortiguamiento grande; y c) con un amortiguamiento pequeño. Éste último tiene un rango grande de
aplicaciones, en diversos mecanismos, tanto para casos prácticos, como por ejemplo, controlar el abrir
y cerrar puertas; y para eliminar oscilaciones perjudiciales en dispositivos mecánicos, entre otros
muchos. Para tener una idea de los alcances de estos sistemas, las figuras 4 (a y b), ilustran un
dispositivo (a) fundamentado en ésta discusión, y en (b) una aplicación del dispositivo.
Ahora, si tenemos en cuenta que, físicamente, en términos oscilatorios, ωo debe ser mayor, o en el peor
de los casos, ser igual a γ; entonces podemos reescribir, x(t) como
x(t) = = e-γt/2 [A Exp.{- (ωo2 - γ2/4)1/2}t + B Exp.- {- (ωo2 - γ2/4)1/2}t]
x(t) = e-γt/2[A eiωt + B e-iωt]
con
ω = (ωo2 - γ2/4)1/2 es la frecuencia angular amortiguada
Si tenemos en cuenta, la relación de Euler, eiωt = cos ωt + i Sen ωt, e igualmente
e-iωt = Cos ωt – i Sen ωt, podemos escribir la solución, como
x(t) = e-γt/2[(A + B) Cos ωt + i(A – B) Sen ωt]
si hacemos las constantes A + B = C1, y C2 = i(A – B), entonces la función se escribirá como
x(t) = e-γt/2[C1 Cos ωt + C2 Sen ωt]
Incluyendo un ángulo de fase, α, con las mismas características del ángulo de fase, utilizado para el
movimiento armónico; tenemos, C1 = C Cos α, y C2 = C Sen α, la función solución la podemos
escribir como
x(t) = C e-γγt/2Cos (ω
ωt + α)
(a)
(a)
(b)
(c)
Figura 3
Estudiante. En algunos libros he visto que en la constante de amortiguamiento incluyen un 2, pero no
entiendo de dónde sale ese 2.
Profesor. Si efectivamente, algunos autores hacen eso, pero es sólo por comodidad, no hay ninguna
otra razón. Para no crear esas dudas, yo prefiero usar sólo aquellos parámetros que tengan algún sentido
físico. Pues no le veo tanta utilidad a la inclusión de ese 2.
Estudiante. Ahora se puede apreciar muy bien la diferencia entre los sistemas oscilatorios ideales y
reales; pues aunque el carácter oscilatorio sigue prevaleciendo, por la función oscilatoria, seno o
coseno, que describe la evolución temporal del movimiento; en su amplitud, está justificado como se
disipa la energía de estos sistemas.
Profesor. Efectivamente, aunque entre los prefactores: A (para el movimiento armónico simple) y Ceγt/2
(para el amortiguado), y la fase de las funciones oscilatorias, se pueden establecer sus propias
relaciones; en razón a que nuestro interés fundamental está en el proceso de disipación de la energía de
los sistemas oscilatorios, nos referiremos sobre todo a ella. Vimos en la primera parte del curso que la
energía en el movimiento armónico simple esta dada por E = kA2/2 (constante); ahora para los sistemas
amortiguados E = k(C e-γt/2)2/2 = kC2e-γt/2 = Eoe-γt = E(t), con Eo = kC2/2; la energía inicial, o energía
de perturbación del sistema.
(a)
(b)
Figura 4
Estudiante. Eso quiere decir que, ¿ésta es la descripción de los movimientos oscilatorios reales?
Profesor. En la primera aproximación, sí; pues no se puede olvidar que por ejemplo, en la constante
del término disipativo de la ecuación de movimiento, b, incluimos factores que están relacionados con
la disipación de energía, pero que el tratar de incluirlos en una sola expresión matemática, nos
conduciría a algo muy complejo. Y eso, asumiendo que todos los factores pudieran ser de alguna
manera, mensurables o cuantificables.
Estudiante. Con la solución que se ha obtenido, podemos saber, ¿cuánto tiempo tarda un sistema
oscilatorio, que ha sido perturbado con una determinada energía Eo, en dejar de oscilar totalmente?
Profesor. Buena pregunta, para buscar una respuesta, miremos la expresión de la energía E(t) = Eoe-γt,
ya que si el sistema oscila, es porque en él hay energía, ¿puede ser E(t) = 0, en algún momento?
Estudiante. Pienso que eso será, sólo cuando e-γt = 0
Profesor. ¿Cuándo se cumple eso?
Estudiante. Si la reescribimos como, 1/eγt; se puede ver, que sólo cuando t sea infinito, o mejor,
cuando t, tienda a infinito.
Profesor. Eso es lo que se puede decir, en términos matemáticos. Pero obviamente, en la realidad, las
cosas no son así. No obstante, para darle una interpretación física al problema, usando esa forma de la
energía, se ha optado por definir una cantidad apropiada para el caso, es el tiempo de vida medio del
sistema, designado por, τ. Ese tiempo es, el que tarda un sistema para que su energía inicial Eo, se
reduzca a Eo/e; es decir, cuando γt = 1, o sea, t = 1/γ. Así que, el tiempo de vida media del sistema será,
τ = 1/γ.
Estudiante. Bueno profesor, yo soy un estudiante de ingeniería, y como usted nos ha dicho, quiero ser
ingeniero con mi visión actualizada, puesta en el siglo XXI, quiero tener a mi disposición todo este
conocimiento fundamental, para utilizarlo en mi campo de acción. ¿Cómo puedo visualizar la
importancia y utilidad de éste conocimiento?
Profesor. Me parece muy pertinente su inquietud. Al respecto puedo reafirmar lo que siempre vengo
diciendo, es muy importante tener grandes metas en la vida, diferentes a las de sólo obtener diplomas;
pues si bien el titulo te abre puertas, el conocimiento que debe justificar ese diploma, le permite crecer,
y continuamente tener apetito de crecimiento. Cuando tienes grandes metas, todos los asuntos
relacionados con tu formación, deben tener para usted el máximo interés. Como se los he dicho tantas
veces; solo podemos aplicar aquello que entendamos muy bien, pues de esa manera, se gana la
seguridad necesaria para hacer uso del conocimiento.
Para tratar de ver el uso de los conceptos discutidos aquí, primero miremos la relación que el tema tiene
con otros conceptos aparentemente diferentes; por ejemplo, los sistemas electrónicos. En electrónica,
hay unos elementos muy simples, que tienen gran utilidad en sus diferentes dispositivos; me refiero a:
el condensador, la resistencia y el inductor. La figura 5 muestra una ilustración de tales elementos.
(a)
(b)
(c)
Figura 5
En el curso de electromagnetismo usted debe haber aprendido, lo que representa físicamente cada uno
de estos elementos; por lo que no entraré en detalle sobre ellos aquí, y sólo me limitaré a decir, muy
brevemente, el papel que cada uno cumple en un circuito simple. La figura 6 (a y b) muestra dos
esquemas interesantes; en (a) un circuito, normalmente, llamado, LC, que incluye un condensador y un
inductor; en (b) se muestra un sistema mecánico equivalente, masa-resorte.
Considerando en los dos sistemas el caso ideal; como es ya claro, en el movimiento armónico simple,
consideramos sólo las propiedades de cada elemento: la inercia de la masa, la constante del resorte; en
el circuito LC: la capacitancia, C, y la inductancia, L.
Estudiante. En el sistema masa-resorte, ya es claro su tratamiento; pero en el circuito LC, ¿qué papel
juega el conductor que conecta al condensador y el inductor?
(a)
(b)
Figura 6
Profesor. Como se anotó inicialmente cuando discutimos el oscilador armónico, un vacío absoluto, es
como una imposibilidad física, entonces siempre existirá algo que represente resistencia al movimiento,
y que justifique en éste sistema, la no existencia del movimiento perpetuo. Igualmente en el circuito,
LC, los conductores se asume que son excelentes, como para que no le ofrezcan resistencia a las cargas
eléctricas; eso también es ideal. En esos términos, los dos sistemas son equivalentes.
Ahora, perturbamos el circuito, cargando el condensador con una carga q, con lo que introducimos al
sistema una diferencia de potencial V; en tanto que al sistema masa-resorte, lo perturbamos aplicando
una fuerza externa, FExt., a través de la cual se le da al sistema una energía, E. Entonces las ecuaciones
dinámicas equivalentes para estos sistemas serán:
Para el circuito LC, las caídas de potencial en Para el sistema masa-resorte, una vez
perturbado, la fuerza neta será nula, así que
cada elemento son
VC = q/C y VL = Ldi/dt = Ld2q/dt2
FExt. = md2x/dt2 = - kx ⇒ ωo 2 = k/m
Como hay conservación de la energía
Reescribiendo la ecuación, tenemos
VC + VL = q/C + Ld2q/dt2 = 0
d2x/dt2 + ωo2 x = 0
Reescribiendo esta ecuación, tenemos
Función solución: x(t) = xo Sen (ωot + θ)
en el equilibrio
d2q/dt2 + ωoq = 0 ⇒ ωo2 = 1/LC
Función solución: q(t) = qo Sen (ωot + θ)
De acuerdo con las últimas ecuaciones en cada columna, ¿qué comparación puede hacer usted entre
estos sistemas?
Estudiante. Lo que puedo decir es que; en el sistema eléctrico la variable independiente q (carga
eléctrica), equivale en el sistema masa-resorte (mecánico) a x; y que las constantes ωo2 =1/LC, equivale
a ωo2 = k/m, respectivamente.
Profesor. Muy bien. Esto muestra que todos los conceptos discutidos desprevenidamente en los cursos,
tienen su sentido fundamental, y en todos los campos aplicados tienen su utilización, sólo que
necesitamos insistir en esa dirección, para que en los cursos de ingeniería, se aprecie verdaderamente
su importancia, y por lo tanto se despierte el mayor interés por estos cursos.
Miremos ahora el caso real, considerando el circuito RLC de las figuras 7 (a) y (b)
(a)
Resistencia
(b)
Figura 7
Análoga a la ecuación planteada para la fig. 7, sólo que ahora incluimos la resistencia que encuentran
los portadores de carga en el proceso de conducción (a), equivalente a la resistencia que ofrece el
medio, al movimiento del sistema masa-resorte, (b), en el circuito RLC, la caída de potencial en cada
elemento, y las correspondientes fuerzas en (b) son:
Figura 7(a)
Figura 7(b)
VC = q/C;
VR = iR;
VL = Ldi/dt
FExt. = ma;
FElast. = -kx;
Fdis. = - bv
Ld2q/dt2 + Rdq/dt + q/C = 0
md2x/dt2 + bdx/dt + kx = 0
d2q/dt2 + (R/L)dq/dt + q/LC = 0
d2x/dt2 +( b/m)dx/dt + (k/m)x = 0
d2q/dt2 + γdq/dt +ωo q = 0
d2x/dt2 +γdx/dt + ωo x = 0
Función solución: q(t) = qoe-γt/2Cos(ωt + α)
En el equilibrio
Función solución: x(t) = xoe-γt/2Cos(ωt + α)
Estudiante. Según esto, veo que matemáticamente, no hay ninguna diferencia en el tratamiento de los
dos casos, ¿eso es válido en general?
Profesor. Efectivamente, es sólo establecer las variables y parámetros equivalentes entre los sistemas,
y no sólo en éste ejemplo; pues la matemática es la misma. De hay en adelante, es analizar las
soluciones para las diferentes situaciones que sean de interés general o particular.
Los conceptos discutidos constituyen algunos fundamentos que usted tiene ahora que utilizar, no solo
para afianzar su comprensión, sino para apreciar su utilidad, y ganar mucha confianza en su aplicación.
Para eso, en el taller correspondiente (Taller 1), tiene en los ejercicios propuestos, la oportunidad de
lograr buena parte de esa destreza que debe ganar con el este curso; recuerde que, el único que gana
con su trabajo, es usted.






