CONVEXIDAD
Anuncio

Conjuntos convexos
♦ Ejemplos de conjuntos convexos en R2
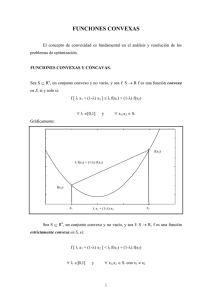
CONVEXIDAD
♦ DEFINICION: Un conjunto A es convexo
♦Conjuntos convexos
♦Convexidad de funciones
λx + (1 − λ ) y
cuando
∀ x, y ∈ A y ∀λ ∈ [0,1] se cumple
λx + (1 − λ ) y ∈ A
♦ Conjunto convexo:
R2
y
λ =0
λ = 1/ 2
x
λ =1
♦ Conjuntos no convexos:
Cualquier segmento que una puntos que pertenezcan al
conjunto, está completamente contenido dentro del
propio conjunto
Combinación lineal convexa de
m puntos
x1 , x 2 ,K, x m ∈ R n
x = λ1x1 + λ2 x 2 + K + λm x m siendo
λ1 ≥ 0, λ2 ≥ 0,..., λm ≥ 0
λ1 + λ2 + K + λm = 1
Combinaciones
lineales convexas
Combinaciones
lineales convexas
1
Poliedro convexo generado por
un conjunto de puntos
♦ Conjunto formado por todas las
combinaciones lineales convexas (CLC) de los
puntos generadores
Propiedades de los conjuntos
convexos
♦ En general, ni la unión ni la diferencia de
conjuntos convexos produce un conjunto
convexo
Propiedades de los conjuntos
convexos
♦ Un conjunto es convexo si y solo si toda
CLC de puntos del propio conjunto
pertenece al conjunto
♦ La intersección de conjuntos convexos
sigue siendo un conjunto convexo
Envoltura convexa de un
conjunto
♦ Es el menor conjunto convexo que lo
contiene
♦ Intersección de todos los conjuntos
convexos que lo contienen
Vértices de un conjunto
convexo
Un vértice es un punto del
conjunto que no puede ser
expresado como CLC de
otros dos puntos diferentes
del propio conjunto
2
Tipos especiales de conjuntos
convexos
♦ Hiperplanos
{
}
H = x = ( x1 ,..., xn ) ∈ R n a1 x1 + am x2 + K + am xm = b
{
S = {x = ( x ,..., x ) ∈ R
}
< b}
S = x = ( x1 ,..., xn ) ∈ R a1 x1 + am x2 + K + am xm ≤ b
n
♦ Una función definida sobre un dominio
convexo D, es convexa cuando
∀ x, y ∈ D y ∀λ ∈ [0,1] se cumple
f (λx + (1 − λ ) y ) ≤ λf ( x) + (1 − λ ) f ( y )
♦ Semiespacios
1
Convexidad de funciones
n
n
a1 x1 + am x2 + K + am xm
♦ Polítopos: conjuntos que se expresan
como intersección de un número finito
de semiespacios cerrados
Caso de funciones de una variable
f(x)
♦ Una función definida sobre un dominio
convexo D, es estrictamente convexa
cuando
∀ x, y ∈ D y ∀λ ∈ (0,1) se cumple
f (λx + (1 − λ ) y ) < λf ( x ) + (1 − λ ) f ( y )
Una función es convexa cuando el
segmento que une dos puntos cualesquiera
de la gráfica de la función queda siempre
por encima de la gráfica.
f(y)
Si el segmento queda siempre estrictamente
por encima (salvo en los extremos),
entonces la convexidad es además estricta
λ f( x)+(1-λ) f( y)
f(x)
f(λx+(1-λ)y)
Toda función estrictamente convexa es
también convexa
x
λx+(1-λ)y
y
Diferencia entre convexidad y
convexidad estricta
Función convexa
(no estrictamente)
Función f(x,y)=x2+y2
Función estrictamente
convexa
3
Funciones cóncavas
Funciones cóncavas de una sola variable
♦ Una función definida sobre un dominio
convexo D, es cóncava cuando
∀ x, y ∈ D y ∀λ ∈ [0,1] se cumple
f (λx + (1 − λ ) y ) ≥ λf ( x ) + (1 − λ ) f ( y )
♦ Una función definida sobre un dominio
convexo D, es estrictamente cóncava
cuando
∀ x, y ∈ D y ∀λ ∈ (0,1) se cumple
Función cóncava
(no estrictamente)
Función estrictamente
cóncava
f (λx + (1 − λ ) y ) > λf ( x) + (1 − λ ) f ( y )
Función cóncava de dos variables
Funciones que no son cóncavas ni convexas
Función f(x,y)=1-2x2-3y2
Propiedades de las funciones
convexas
♦ Si f(x) es una función convexa entonces la
función opuesta –f(x) es cóncava, y viceversa
♦ Las funciones lineales son a la vez
cóncavas y convexas, pero no
estrictamente
f ( x1 , x2 , L , xn ) = c1 x1 + c2 x2 + L + cn xn + d
Caso de funciones de una
variable: f(x) = cx+d
f(x)
–f(x)
f(λx+(1-λ)y) = λf(x)+(1-λ)f(y)
4
♦ La suma de funciones convexas sigue siendo
una función convexa
♦ La suma de funciones cóncavas sigue siendo
una función cóncava
♦ Cualquier combinación lineal con coeficientes
positivos de funciones convexas es también
una función convexa
f1 ( x), f 2 ( x), K , f k ( x) funciones convexas
λ1 ≥ 0, λ2 ≥ 0, K , λk ≥ 0
⇒ λ1 f1 ( x) + λ2 f 2 (x) + L + λk f k ( x) es convexa
♦ Si una función h(x) es lineal (cóncava y
convexa) entonces los siguientes
conjuntos son siempre convexos
S k = {x h( x) ≤ k }
Semiespacio
Tk = {x h( x ) ≥ k }
Semiespacio
H k = {x h( x ) = k }
Hiperplano
Relación entre conjuntos y
funciones convexas
♦ Si una función f(x) es convexa entonces
S k = {x f ( x) ≤ k }
es un conjunto convexo para cualquier
valor de k
♦ Si una función g(x) es cóncava entonces
Tk = {x g ( x) ≥ k }
es un conjunto convexo para cualquier
valor de k
EJEMPLO:
Para estudiar si el siguiente conjunto es convexo
⎧
x12 + 3 x2 ≤ 10 ⎫
⎪⎪
⎪⎪
A = ⎨( x1 , x2 ) x1 − 2 x12 − x22 ≥ 7 ⎬
⎪
5 x1 + 2 x2 = 15 ⎪⎪
⎪⎩
⎭
bastaría comprobar que:
f ( x1 , x2 ) = x12 + 3 x2
es una función convexa
g ( x1 , x2 ) = x1 − 2 x − x22 es una función cóncava
2
1
h( x1 , x2 ) = 5 x1 + 2 x2
es una función lineal
Estudio de la convexidad de
funciones diferenciables
Clasificación de matrices
simétricas
♦ Se puede estudiar la convexidad a partir del
♦ Una matriz cuadrada simétrica A se dice...
– Semidefinida positiva cuando xTAx ≥ 0 para
cualquier vector x
– Semidefinida negativa cuando xTAx ≤ 0 para
cualquier vector x
– Definida positiva cuando xTAx > 0 para cualquier
vector x no nulo
– Definida negativa cuando xTAx < 0 para cualquier
vector x no nulo
– Indefinida cuando la expresión xTAx toma valores
positivos o negativos dependiendo del vector x
estudio de la matriz hessiana
⎛ ∂2 f
⎜
2
⎜ ∂x1
⎜ ∂2 f
Hf ( x1 , x2 ) = ⎜ ∂x x
⎜ 2 1
⎜ L
⎜ ∂2 f
⎜ ∂x x
⎝ n 1
∂2 f
∂x1 x2
∂2 f
∂x22
L
∂2 f
∂xn x2
∂2 f ⎞
⎟
∂x1 xn ⎟
2
∂ f ⎟
L
⎟
∂x2 xn ⎟
L
L ⎟
∂2 f ⎟
L
∂xn2 ⎟⎠
L
Bajo ciertas condiciones de regularidad, la matriz
hessiana de una función es una matriz simétrica
5
Clasificación a partir de los
autovalores
♦ Los autovalores de la matriz A son las
raíces del polinomio característico:
a11 − λ
det( A − λI ) =
a21
L
an1
a12
L
a22 − λ L
L
L
an 2
a1n
a2 n
L
= 0 ⇒ λ1 , λ2 ,..., λn
L ann − λ
Los autovalores de una matriz simétrica
son siempre números reales
Clasificación a partir de los
menores principales
♦ Los menores principales de la matriz A son n
números reales obtenidos de la siguiente
forma:
♦ Si todos los menores son diferentes de cero, salvo
posiblemente el último, pero ni son todos positivos ni
se alternan en el signo, entonces la matriz es
indefinida.
Cuando existe un menor nulo que no es el
último el criterio de los menores principales
no permite clasificar la matriz
Ejemplo:
∆1 = 12 >0
∆2 = 0
∆3 = 5 > 0
∆4 = 0
♦ Una vez calculados los autovalores de una
matriz simétrica, se tiene:
– A es definida positiva si y solo si los autovalores
son todos estrictamente positivos.
– A es definida negativa si y solo si los autovalores
son todos estrictamente negativos.
– A es semidefinida positiva si y solo si los
autovalores son todos mayores o iguales a cero.
– A es semidefinida negativa si y solo si los
autovalores son todos menores o iguales a cero.
– A es indefinida si existen dos autovalores de
diferentes signos.
♦ A es definida positiva si y solo si todos los menores
principales son estrictamente positivos:
∆1 > 0, ∆2 > 0, ∆3 > 0,..., ∆n > 0
♦ A es definida negativa si y solo si los menores son
todos ellos no nulos y de signo alterno, siendo
siempre el primero negativo:
∆1 < 0, ∆2 > 0, ∆3 < 0, ∆4 > 0,...
♦ Si todos los menores son estrictamente positivos
salvo el último que es nulo, entonces la matriz A es
semidefinida positiva.
∆1 > 0, ∆2 > 0, ∆3 > 0,..., ∆n = 0
♦ Si los menores son todos de no nulos, salvo el último,
y además de signo alterno, siendo el primero
negativo, entonces A es semidefinida negativa.
∆1 < 0, ∆2 > 0, ∆3 < 0, ∆4 > 0,..., ∆n = 0
Estudio de la convexidad de la función
a partir de la clasificación de su matriz
hessiana
♦ f(x) es convexa si y solo si Hf(x) es
semidefinida positiva para cualquier x en el
dominio de la función.
♦ f(x) es cóncava si y solo si Hf(x) es
semidefinida negativa para cualquier x.
♦ Si Hf(x) es definida positiva para cualquier x
entonces f(x) es estrictamente convexa.
♦ Si Hf(x) es definida negativa para cualquier x
entonces f(x) es estrictamente cóncava.
6