Ejercicios T4
Anuncio

Tema 4
Solución Ejercicio 3b
•
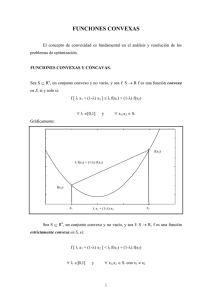
Teorema de Weierstrass
La función objetivo es continua.
El conjunto de soluciones factibles viene dado por:
𝑆 = 𝐷 ∩ 𝑋 = 𝑋 = {(𝑥, 𝑦) ∈ ℝ2 | 2𝑥 + 𝑦 ≤ 1, 𝑥 ≥ 0}
S
Gráficamente se aprecia que S, al ser cerrado pero no acotado, no es compacto.
Al no verificarse el teorema, no podemos concluir nada sobre la existencia de óptimos
globales.
•
Teorema Local-Global
S viene definido por la intersección de dos semiespacios, luego S es un
conjunto convexo. Gráficamente se aprecia también que se trata de un conjunto
convexo, ya que es posible ir de un punto a otro de él en línea recta sin salirse de él.
La matriz Hessiana de la función objetivo es:
2
0
𝐻 𝑓 (𝑥, 𝑦) = �
�
0 12𝑦 2
Si utilizamos el criterio de los autovalores (𝜆1 > 0, 𝜆2 ≥ 0) obtenemos que H es una
matriz semidefinida positiva y, en consecuencia, que f es una función convexa.
En consecuencia, el Teorema permite concluir que de existir un mínimo, éste va a ser global
(pero no estricto).
Solución Ejercicio 3d
•
Teorema de Weierstrass
La función objetivo es continua.
El conjunto de soluciones factibles viene dado por:
𝑆 = 𝐷 ∩ 𝑋 = 𝑋 = {(𝑥, 𝑦) ∈ ℝ2 |
2
S
𝑥2 𝑦2
+ ≤ 2, 𝑥2 + 𝑦2 ≥ 4, 𝑥, 𝑦 ≥ 0}
8
2
4
Gráficamente se aprecia que S es un conjunto compacto, al ser cerrado y acotado.
Al verificarse el teorema podemos concluir que existe al menos un óptimo global.
•
Teorema Local-Global
Gráficamente se aprecia que S no es un conjunto convexo, ya que existen
puntos de S desde los cuales no es posible ir en línea recta a otros del mismo sin
salirse de él.
El Teorema no se cumple y, en consecuencia, no podemos concluir nada.
Solución Ejercicio 5d
Pasos:
1º Conjunto de soluciones factibles:
2º Curvas de nivel:
𝑆 = 𝐷 ∩ 𝑋 = 𝑋 = {(𝑥, 𝑦) ∈ ℝ2 | 𝑦2 ≤ 𝑥 + 1, |𝑦| ≥ 1, 𝑥 ≥ 0}
𝐷 = {(𝑥, 𝑦) ∈ ℝ2 }
𝐶𝑁 = {(𝑥, 𝑦) ∈ 𝐷| 𝑥2 + 𝑦2 = 𝑐 }
Las curvas de nivel son circunferencias concéntricas respecto del origen.
3º Vector gradiente:
∇𝑓(𝑥, 𝑦) = �
2𝑥
�
2𝑦
2
−2
Así, por ejemplo, ∇𝑓(1,0) = � � y ∇𝑓(−1,0) = � �.
0
0
MIN (0,1)
y
S
x
S
MIN (0,-1)
Solución Ejercicio 4
En primer lugar analizamos si S es convexo. Para ello, determinamos dicho conjunto:
𝑆 =𝐷∩𝑋
𝐷 = {(𝑥, 𝑦) ∈ ℝ2 }
𝑋 = {(𝑥, 𝑦) ∈ ℝ2 | 𝑥 + 𝑦 = 3, 𝑎𝑥 2 + 𝑦 2 ≤ 4, 𝑎𝑦 2 − 𝑥 2 ≥ 6}
•
•
•
•
𝑆 =𝐷∩𝑋 =𝑋
𝑥 + 𝑦 = 3 define un hiperplano y, por tanto, un conjunto convexo.
Según la propiedad 5 de funciones convexas, para que 𝑎𝑥 2 + 𝑦 2 ≤ 4 defina un
conjunto convexo 𝑔2 (𝑥, 𝑦) = 𝑎𝑥 2 + 𝑦 2 tiene que ser una función convexa (o
estrictamente convexa). Para saber en qué casos podría darse, hallamos su
matriz Hessiana:
2𝑎 0
𝐻 𝑔2 (𝑥, 𝑦) = �
�
0 2
Aplicando el método de los autovalores, para que 𝑔2 sea una función convexa
(o estrictamente convexa) 𝐻 𝑔2 (𝑥, 𝑦) tiene que ser DEFINIDA + o
SEMIDEFINIDA +. Por lo tanto, deberá cumplirse que 𝑎 ≥ 0.
Según la propiedad 6 de funciones convexas, para que 𝑎𝑦 2 − 𝑥 2 ≥ 6 defina un
conjunto convexo 𝑔3 (𝑥, 𝑦) = 𝑎𝑦 2 − 𝑥 2 tendrá que ser una función cóncava (o
estrictamente cóncava). Para saber en qué casos puede darse, hallamos su
matriz Hessiana:
−2 0
𝐻 𝑔2 (𝑥, 𝑦) = �
�
0 2𝑎
Aplicando el método de los autovalores, para que 𝑔3 sea una función cóncava
(o estrictamente cóncava) 𝐻 𝑔3 (𝑥, 𝑦) tendrá que ser DEFINIDA - o
SEMIDEFINIDA -. Por lo tanto, deberá cumplirse que 𝑎 ≤ 0.
De acuerdo con lo anterior, S será un conjunto convexo para 𝑎 = 0.
En relación a la función objetivo, para que el óptimo sea global estricto la función tiene que ser
estrictamente convexa o estrictamente cóncava. Para saber si esto es posible, hallamos su
matriz Hessiana:
2 1
𝐻 𝑓 (𝑥, 𝑦) = �
�
1 2𝑏
Aplicando el criterio de los menores principales, puesto que ∆1 = 2 > 0, 𝑓 solamente puede
ser estrictamente cónvexa. Por tanto, deberá cumplirse ∆2 = 4𝑏 − 1 > 0, esto es, 𝑏 > 1⁄4.
En definitiva, el programa matemático tendrá solución única y global para 𝑎 = 0 y 𝑏 > 1⁄4.