Abundancia Relativa de Especies
Anuncio

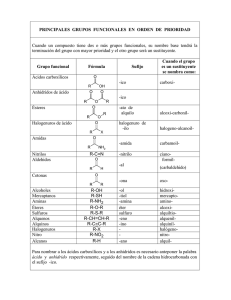
Abundancia Relativa de Especies Cuando una especie química “A” intercambia partículas “L” con el medio, se pueden formar una serie de compuestos de fórmula ALn. Cuál de estas especies es la que predomina depende de la concentración de “L” en el medio. Se puede predecir facilmente este predominio usando las constantes logarítmicas de disociación sucesiva (pKa ó pKc), pero también se puede calcular la proporción relativa de cada especie en forma cuantitativa. Predicción Cualitativa La disociación de los compuestos ALn se representa por los equilibrios: ALn-1 + L ALn Las constantes sucesivas son: K c, n = A L n −1 L ALn Podemos afirmar que en medios muy diluídos en L (pL>pK1), predomina la especie libre “A”, mientras que en medios muy concentrados (pL<pKn) predomina el complejo con mas moléculas de “L” (donador). En los valores intermedios dominan los anfolitos: ALn ... ... pK... pKn AL2 pK3 AL pK2 A pK1 pL Cuando llega a ocurrir que pKm+1>pKm, entonces el anfolito intermedio ALm dismuta: ALm+1 ALm ALm ALm-1 pKm+1 pKm pL En estos casos, el resultado final será que predominan ALm+1 y ALm-1, solo quedan trazas de ALm. ALm+1 ALm-1 pL pKnuevo El pK del nuevo par será la media ponderada de los anteriores. Cálculo Numérico La formación de las especies ALn se representa por: ALn A + nL Las constantes globales de formación son: βn = ALn A L n Si definimos un nuevo término αM como el cociente de la conc. total de S, respecto a la conc. libre: αA = αA( L) = A T A + ∑ ALn = A A se puede demostrar que este tiene la forma: α A = α A ( L) = 1 + ∑ β n L n Por lo tanto, la fracción de la especie en forma libre queda representada por la expresión: φA = 1α A Las demás especies estarián representadas por: φ ALn = φ Aβ n L n El sistema de ecuaciones obtenido indica que la fracción existente de cada especie depende únicamente de la concentración de L (pL). Ejemplo básico Supongamos una especie M, la cual puede formar con L los complejos ML y ML2, según los equilibrios: ML L M L2 ML + L K c , 2 = ML2 ML M + L K c ,1 = M L ML Cualitativamente esperamos tres regiones de predominio de especies, excepto cuando ML sea inestable y dismute, estas serán: cuando pKc,1>pKc, ML2 Y cuando pKc,1<pKc,2: ML pKc,2 ML2 M pKc,1 M pL pL (pKc,1 + pKc,2) 2 Para conocer la fracción relativa de cada especie a diferentes valores de pL, necesitamos plantear el siguiente sistema de ecuaciones: β1 = 1 K c ,1 β2 = 1 K c ,1 ⋅ K c , 2 L = 1 0 − pL α M = 1 + β1 L + β 2 L φ M = 1α M φ M L = φ M β1 L φ M L = φ M β2 L 2 2 2 En las figuras de abajo se muestran los resultados obtenidos para diversos valores de pKc,1 y pKc,2. pKc,2=3, pKc,1=7 pKc,2=4, pKc,1=7 pKc,2=5, pKc,1=7 pKc,2=6, pKc,1=7 De las imágenes anteriores se concluye que para que la especie intermedia ML llegue a ser prácticamente la única especie en solución y M y ML2 sean despreciables, se necesita colocarse a un valor de pL intermedio entre PKc,1 y pKc,2 y además, la diferencia entre los pK’s debe ser mayor a tres unidades.