CAPÍTULO 7: INFERENCIA PARA PROPORCIONES Y MEDIAS
Anuncio

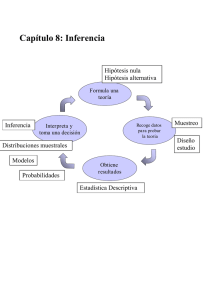
Página 1 de 13 CAPÍTULO 7: INFERENCIA PARA PROPORCIONES Y MEDIAS En este capítulo entraremos al final del ciclo del método científico, usando la información de la muestra para generalizar y llegar a conclusiones acerca de la población de interés. Recordemos algunas definiciones: Parámetro es una medida de resumen numérica que se calcularía usando todas las unidades de la población. Es un número fijo. Generalmente no lo conocemos. Estadística es una medida de resumen numérica que se calcula de las unidades de la muestra. El valor de la estadística se conoce cuando tomamos una muestra, pero varia de muestra en muestra variación muestral. Inferencia estadística: es el proceso de sacar conclusiones acerca de la población basados en la información de una muestra de esa población. Objetivos de la inferencia: estimación de parámetros, intervalos de confianza y docimasia, prueba o test de hipótesis (o prueba de significación estadística). La estimación de parámetros consiste en el cálculo de estadísticas en muestras, con el fin de obtener información sobre el valor de los parámetros de la población. Esta inducción se basa en la teoría de probabilidades y sólo es posible cuando se conoce la conducta o "distribución muestral" de las estadísticas. La docimasia de hipótesis consiste en conocer la probabilidad de ocurrencia, bajo la hipótesis nula, del resultado obtenido en la investigación, basándose en la distribución muestral de la estadística utilizada para medir tal resultado. Inferencia Simple para Proporciones Tomando decisiones acerca de la proporción de una población Primero revisemos el caso donde lo que nos interesa es investigar sobre una proporción de una población. Ejemplo Embarazo adolescente En el año 2000, el 16% de las embarazadas era en adolescentes menores de 20 años de edad, ¿Habrá aumentado esta cifra? Escriba las hipótesis nula y alternativa que usaría para probar la aseveración anterior. Las hipótesis deben ser expresadas en términos del parámetro P, la proporción de interés en la población. Hipótesis: H0 : versus H1 : Acá, nuestro parámetro de interés es el porcentaje de embarazadas que son adolescentes menores de 20 años, es decir, P=0.16. Página 2 de 13 Para resolver, se considera una muestra de 704 partos ocurridos en el Hospital de Talca, donde 132 de ellos corresponden a embarazadas que son Adolescentes menores de 20 años de edad. Con la información anterior, es posible determinar el porcentaje observado en la muestra de los embarazos que corresponden a Adolescentes menores de 20 años de edad, siendo 132 ˆ= p = 0,1875 . 704 Para la obtención del valor-p, se requiere conocer la distribución probabilística de la proporción muestral p̂ : Distribución muestral de p̂ , la proporción muestral Si P representa la proporción de elementos en una población con alguna característica. Tomamos una muestra aleatoria simple de tamaño n de esa población y si n es “suficientemente” grande (cuando nP ≥ 5 y n(1 − P ) ≥ 5 ) , entonces la distribución de la proporción muestral p̂ es aproximadamente normal: ˆ~ & N P , p P(1 - P ) entonces la proporción muestral estandarizada es: n Z= ˆ- P p P (1 − P ) n & N(0, 1) ~ Test Z para una proporción en la población • Al docimar una hipótesis acerca del parámetro en la población P, la hipótesis nula es H0 : P = p0 , donde p0 es un valor hipotético de P. • Supuestos: Se recomienda usar este test cuando los datos provienen de una muestra aleatoria de tamaño n, donde n satisface que np 0 y n(1 − p0 ) es mayor o igual a 5. • Nuestra decisión acerca del parámetro P estará basada en el valor de la proporción muestral estandarizada, la cual es: Z obs = ˆ − p0 p p0 (1 − p0 ) n • Este “score” o puntaje z es el test estadístico, y su distribución bajo H0 es aproximadamente N(0,1) . Notar que el test estadístico no depende de la hipótesis alternativa. • Calculamos el valor-p del test, el cual depende de la dirección de la hipótesis alternativa: Página 3 de 13 Test Unilateral, cola superior Test Unilateral, cola inferior Si H1 : P > p0 , entonces el valor-p es P(Z > z obs ) es el Si H1 : P < p0 , entonces el valor-p es P(Z < z obs ) es el área a la derecha del test estadístico observado bajo H0 . área a la izquierda del test estadístico observado bajo H0 . Test Bilateral Si H1 : P ≠ p0 , entonces el valor-p es 2P(Z > z obs ) el área afuera de las dos colas del test estadístico observado bajo H0 . N(0,1) N(0,1) N(0,1) p-value 2 p-value Z OBS p-value 2 p-value -ZOBS Z Z +ZOBS Z Z OBS • Decisión: Si el valor-p es menor o igual al nivel de significación rechazamos H 0 . En nuestro ejemplo: Hipótesis: H0 : P = 0,16 H1 : P > 0,16 El Test Estadístico Observado está dado por: Z obs = ˆ − p0 p p0 (1 − p0 ) n = 0,1875 − 0,16 0,16 ( 1 − 0,16 ) 704 = 1,99 La dirección del extremo es hacia el lado derecho, luego el valor-p: Valor − p = P [ Z > 1,99 ] = 1 − P [ Z ≤ 1,99 ] = 1 − 0,9767 = 0,0233 Decisión: El valor-p resultó ser del 2,33%, cuyo valor es menor al nivel de significación del 5%, luego, existe evidencia para rechazar la H0 . Conclusión: Por lo anterior, se concluye que ha aumentado el porcentaje de embarazadas que son Adolescentes menores de 20 años de edad. Página 4 de 13 Inferencia Simple para Medias Tomando decisiones acerca de la media de una población Ahora veremos el caso donde lo que nos interesa es investigar sobre la media de una población. Ejemplo Monóxido de Carbono La Comisión Federal de Comercio (Federal Trade Commission http://www.ftc.gov/bcp/menu-tobac.htm) de Estados Unidos clasifica anualmente las variedades de cigarrillos según su contenido de alquitrán, nicotina y monóxido de carbono. Se sabe que estas tres sustancias son peligrosas para la salud de los fumadores. Estudios anteriores han revelado que los incrementos en el contenido de alquitrán y nicotina de un cigarrillo van acompañados por un incremento en el monóxido de carbono emitido en el humo de cigarrillo. Sea µ = media de monóxido de carbono en la población de todos los paquetes de cigarrillos. En el pasado esa media ha sido 15 mg, con una desviación estándar de 4,8 mg y queremos saber si la media actual µ es menor que la media antigua de 15 mg. Escriba las hipótesis nula y alternativa que usaría para probar la aseveración anterior. Las hipótesis deben ser expresadas en términos del parámetro µ, la media de la población de interés. Hipótesis: H0 : versus H1 : Acá, nuestro parámetro de interés es la media de monóxido de carbono en la población de todos los paquetes de cigarrillos. Para resolver, se requiere una muestra, la cual se describe a continuación: La base de datos contiene los datos sobre monóxido de carbono (en miligramos) en una muestra de 25 marcas de cigarrillos (con filtro). MARCA Alpine Benson & Hedges Bull Dirham Camel Lights Carlton Chesterfield Golden Lights Kent Kool L&M Lark Lights Marlboro Merit CO 13,6 16,6 23,5 10,2 5,4 15,0 9,0 12,3 16,3 15,4 13,0 14,4 10,0 MARCA Multifilter Newport Lights Now Old Gold Pall Mall Lights Raleigh Salem Ultra Tareyton True Viceroy Rich Lights Virginia Slims Winston Lights CO 10,2 9,5 1,5 18,5 12,6 17,5 4,9 15,9 8,5 10,6 13,9 14,9 Página 5 de 13 40% Porcentaje 30% 20% 10% 0 5 10 15 20 25 Monóxido de Carbono (mg) Estadísticos descriptivos N CO N válido (según lista) Media 12.528 25 25 Desv. típ. 4.7397 Según la información proporcionada, se tiene: n = 25 x = 12,528 s = 4,7397 Para la obtención del valor-p, se requiere conocer la distribución probabilística del promedio muestral x : Distribución muestral del x , el promedio muestral Si tomamos una muestra aleatoria simple de tamaño n de una población con media desviación estándar σ, donde σ es conocida, y ... µ y ...si la población original distribuye normal, σ x ~ N µ, n Z= x −µ σ ~ N (0,1) n ...si la población original no es necesariamente normal, pero el tamaño muestral es suficientemente grande, x −µ σ Z= es aprox. N (0,1) . x es aprox. N µ, (TCL) σ n n Página 6 de 13 Test Z para la media de una población con σ conocida • Al docimar una hipótesis acerca de la media poblacional µ, la hipótesis nula es H0 : µ = µ0 , donde µ0 es un valor hipotético de µ. • Asumimos que los datos provienen de una muestra aleatoria de tamaño n, de una población con distribución Normal con desviación estándar σ conocida. El supuesto de normalidad no es crucial si el tamaño de la muestra es grande. • Nuestra decisión acerca de estandarizada µ estará basada en el valor de la media muestral x , la cual es: Z obs = x − µ0 σ n • Este “score” o puntaje z es el test estadístico y su distribución bajo H 0 es aproximadamente N ( 0,1) . Notar que el test estadístico no depende de la hipótesis alternativa • Calculamos el valor-p del test, el cual depende de la dirección de la hipótesis alternativa: Test Unilateral, cola superior Test Unilateral, cola inferior Si H1 : µ > µ 0 , entonces el Si H1 : µ < µ 0 , entonces el valor-p es P(Z > z obs ) es el valor-p es P(Z < z obs ) es el área a la derecha del test estadístico observado bajo H0 . área a la izquierda del test estadístico observado bajo H0 . Test Bilateral Si H1 : µ ≠ µ 0 , entonces el valor-p es 2P(Z > z obs ) el área afuera de las dos colas del test estadístico observado bajo H0 . N(0,1) N(0,1) N(0,1) p-value 2 p-value Z OBS • p-value 2 p-value Z Z -ZOBS +ZOBS Z OBS Decisión: Si el valor-p es menor o igual al nivel de significación se rechaza H0 . En nuestro ejemplo: Hipótesis: H0 : µ = 15 H1 : µ < 15 Z Página 7 de 13 El Test Estadístico Observado está dado por: Z obs = x − µ0 σ = n 12,528 − 15 = − 2,58 4,8 25 La dirección del extremo es hacia el lado izquierdo, luego el valor-p: Valor − p = P [ Z < − 2,58 ] = 0,0049 Decisión: El valor-p resultó ser el 0,49%, cuyo valor es menor al nivel de significación del 5%, luego, existe evidencia para rechazar la H 0 . Conclusión: Por lo anterior, se concluye que la media actual de monóxido de carbono en la población de todos los paquetes de cigarrillos es inferior a 15 mg. ¿Qué ocurre si σ es desconocida? El cálculo del error estándar del promedio muestral incluye a σ, pero casi nunca vamos a conocer la variabilidad en la población en estudio. Cuando se desconoce el σ del universo, el error estándar del promedio debe calcularse a partir de la desviación estándar de la muestra: sx = s n En este caso ya no es lícito trabajar con la distribución normal y la variable normal estándar, z= x −µ σx = x−µ σ n sino que se trabajará con la variable t de Student: t= x −µ x−µ = sx s n Esta variable t sigue una distribución t de Student con (n-1) grados de libertad. Página 8 de 13 Propiedades de la distribución t de Student N(0,1) t(15) t(3) • Los valores de t dependen del número de grados de libertad, los que se determinan a partir del número usado en el denominador para el cálculo de la desviación estándar (s) es decir (n-1). • La función de densidad de la distribución t de Student tiene forma de campana simétrica, similar a la distribución normal N(0,1). • Es un poco más “chata” y tiene “colas más pesadas” que la N(0,1). • Cuando el tamaño de la muestra aumenta, la distribución t de Student se aproxima a la N(0,1). Página 9 de 13 t(df) Area =α 0 tα Tabla: Percentiles de la distribución t de Student gl 1 2 3 4 5 t 0.60 0.325 0.289 0.277 0.271 0.267 t 0.70 0.727 0.617 0.584 0.569 0.559 t 0.80 1.376 1.061 0.978 0.941 0.920 t 0.90 3.078 1.885 1.638 1.533 1.476 t 0.95 6.314 2.920 2.353 2.132 2.015 t 0.975 12.706 4.303 3.182 2.776 2.571 t 0.99 31.821 6.965 4.541 3.747 3.365 t 0.995 63.657 9.925 5.841 4.604 4.032 6 7 8 9 10 0.265 0.263 0.262 0.261 0.260 0.553 0.549 0.546 0.543 0.542 0.906 0.896 0.889 0.883 0.879 1.440 1.415 1.397 1.383 1.372 1.943 1.895 1.860 1.833 1.812 2.447 2.365 2.306 2.262 2.228 3.143 2.998 2.896 2.821 2.764 3.657 3.925 3.841 3.604 3.169 11 12 13 14 15 0.260 0.259 0.259 0.258 0.258 0.540 0.539 0.538 0.537 0.536 0.876 0.873 0.870 0.868 0.866 1.363 1.356 1.350 1.345 1.341 1.796 1.782 1.771 1.761 1.753 2.201 2.179 2.160 2.145 2.131 2.718 2.681 2.650 2.624 2.602 3.106 3.055 3.012 2.977 2.947 16 17 18 19 20 0.258 0.257 0.257 0.257 0.257 0.535 0.534 0.534 0.533 0.533 0.865 0.863 0.862 0.861 0.860 1.337 1.333 1.330 1.328 1.325 1.746 1.740 1.734 1.729 1.725 2.120 2.110 2.101 2.093 2.086 2.583 2.567 2.552 2.539 2.528 2.921 2.898 2.878 2.861 2.845 21 22 23 24 25 0.257 0.256 0.256 0.256 0.256 0.532 0.532 0.532 0.531 0.531 0.859 0.858 0.858 0.857 0.856 1.323 1.321 1.319 1.318 1.316 1.721 1.717 1.714 1.711 1.708 2.080 2.074 2.069 2.064 2.060 2.518 2.508 2.500 2.492 2.485 2.831 2.819 2.807 2.797 2.787 26 27 28 29 30 0.256 0.256 0.256 0.256 0.256 0.531 0.531 0.530 0.530 0.530 0.856 0.855 0.855 0.854 0.854 1.315 1.314 1.313 1.311 1.310 1.706 1.703 1.701 1.699 1.697 2.056 2.052 2.048 2.045 2.042 2.479 2.473 2.467 2.462 2.457 2.779 2.771 2.763 2.756 2.750 40 60 120 0.255 0.254 0.254 0.253 - t 0.40 0.529 0.527 0.526 0.524 - t 0.30 0.851 0.848 0.845 0.842 - t 0.20 1.303 1.296 1.289 1.282 - t 0.10 1.684 1.671 1.658 1.645 - t 0.05 2.021 2.000 1.980 1.960 - t 0.025 2.423 2.390 2.358 2.326 - t 0.01 2.704 2.660 2.617 2.576 - t 0.005 ∞ gl Página 10 de 13 Ejemplo Uso de la Tabla t. a) Encuentre el percentil 99 de la distribución t con 4 gl: t.99(4): b) Encuentre el percentil 10 de la distribución t con 30 gl: t.10(30): c) Encuentre el percentil 95 de la distribución t con ∝ gl: Se observa, por ejemplo, que el percentil 97,5 que en la curva normal corresponde a un valor de z = 1,96, en la distribución de t para 24 grados de libertad corresponde a un t de 2,064. Para n infinito la distribución t de Student es igual a la normal, pero en la práctica cuando el número de observaciones es superior a 30, los valores de z y t ya son tan parecidos que se puede utilizar como aproximación, la distribución normal. Test t simple para la media de una población con • σ desconocida. Estamos interesados en docimar la hipótesis acerca de la media de una población µ. La hipótesis nula es H0 : µ = µ 0 donde µ0 es un valor hipotético para µ. La hipótesis alternativa da la dirección del test. • Se asume que los datos provienen de una muestra aleatoria de tamaño n de una El población con distribución Normal con desviación estándar σ desconocida. supuesto de normalidad no es crucial si el tamaño de la muestra es grande. • Nuestra decisión acerca de estandarizada x , el cual es µ, será en base al valor del promedio muestral t obs = x − µ0 . s n Este es el test estadístico y su distribución bajo H0 , es una distribución t con n-1 grados de libertad. Página 11 de 13 • El valor-p del test, depende de la hipótesis alternativa: Test Unilateral, cola superior Test Unilateral, cola inferior Si H1 : µ > µ 0 , entonces el valor-p es P(t > t obs ) es el Si H1 : µ < µ 0 , entonces el valor-p es P(t < t obs ) es el área a la derecha del test estadístico observado bajo H0 . área a la izquierda del test estadístico observado bajo H0 . Test Bilateral Si H1 : µ ≠ µ 0 , entonces el valor-p es 2P(t > t obs ) el área afuera de las dos colas del test estadístico observado bajo H0 . t(n-1) t(n-1) t(n-1) p-value 2 p-value 2 p-value p-value TOBS TOBS T • T -TOBS +TOBS T Decisión: Si el valor-p es menor que el nivel de significancia entonces rechazamos H0 . Revisión de supuestos del test: Este test de hipótesis asume que los datos provienen de una muestra aleatoria de tamaño n de una población con distribución Normal con desviación estándar desconocida. El supuesto de normalidad no es crucial si el tamaño de la muestra es grande (n > 30). Sin embargo es importante primero describir los datos y verificar presencia de sesgos y valores extremos que pudieran hacer pensar que la distribución de la población no es Normal. Ejemplo Datos del mar Laengelmavesi, Finlandia* Se tiene una muestra de peces que fueron pescados en el mar Laengelmavesi de Finlandia (http://www.amstat.org/publications/jse/datasets/fishcatch.txt). Se está investigando el peso de los peces en kilos. Se quiere docimar la hipótesis de que el peso es menor que 16 kilos. µ = peso medio de los “percas” (perch) en la población en kilos. Estadísticos para una muestra N peso 56 Media 15.839 Desviación típ. 1.3618 Error típ. de la media .1820 *Fuente: Brofeldt, Pekka: Bidrag till kennedom on fiskbestondet i vaera sjoear. Laengelmavesi. T.H.Jaervi: Finlands Fiskeriet Band 4, Meddelanden utgivna av fiskerifoereningen i Finland. Helsingfors 1917 Página 12 de 13 Test estadístico observado: t obs = x − µ0 15,839 − 16 = = −0,885 s 1,3618 n 56 -0,885 nos dice que la media muestral esta a 0,885 errores estándar debajo de la media hipotética de 16. Usando la Tabla t: Ya que el test t observado de -0,885 cae entre el percentil 10 y el 20, en la distribución t con 40 grados de libertad, el valor-p estará entre 0,10 y 0,20. 0,10 < valor − p < 0,20 t(55) t(40) Valor-p -1.303 t 0.10 T -0.885 -0.851 0 OBS t 0.20 En SPSS Comparar Medias > Prueba T para una muestra > Valor de Prueba (16). Prueba para una muestra Valor de prueba = 16 peso t -.883 gl 55 Sig. (bilateral) .381 Diferencia de medias -.1607 95% Intervalo de confianza para la diferencia Inferior Superior -.525 .204 t=-0,883 y 55 grados de libertad, para el test unilateral de cola inferior se obtiene un valor-p de 0,1905 (0,381/2). Por lo tanto con un nivel de significancia del 5% no podemos rechazar H0 . Así, parece que el peso medio de las “percas” en este mar, no es significativamente menor que 16 kilos. Página 13 de 13 En resumen, podemos notar que los pasos en una prueba de hipótesis se repiten, lo que cambia es el parámetro de interés: 1. Establecer la hipótesis 2. Definir el nivel de significación 3. Obtener los datos 4. Definir test estadístico y verificar los supuestos 5. Calcular el test estadístico observado bajo H 0 6. Calcular el valor p 7. Tomar la decisión con respecto a H 0 8. Conclusión del investigador