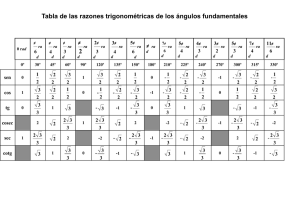
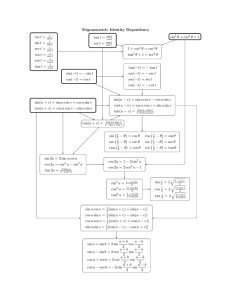
sin (θ) cos (θ) tan (θ) csc (θ) sec (θ) cot (θ)
Anuncio

θ sin (θ) cos (θ) tan (θ) csc (θ) sec (θ) cot (θ) 0 0 1 0 undefined 1 undefined π 6 1 2 √ √ 2 √2 3 π 4 π 3 π 2 2π 3 √ 2 2 3 2 √ 2 2 √ √ 1 2 1 0 undefined − 12 √ − 3 √ 3 2 − √ 2 2 5π 6 1 2 − √ 3 2 π 0 7π 6 − 12 √ 5π 4 − √ 2 2 4π 3 − √ 3 2 3π 2 √ 1 3 2 2 2 3π 4 3 3 −1 5π 3 − √ 3 2 7π 4 − √ 2 2 11π 6 − 12 2π 0 −1 − √ 3 2 − √ 2 2 − 12 3 2 √ 2 √2 3 2 1 undefined √2 3 −2 − √ 3 3 undefined −1 undefined 3 3 −2 − √23 1 √ − 2 √ − 2 − √23 −2 0 √ √ 3 1 2 √ − 3 − √23 2 -1 √ − 2 √ 1 0 √ − 3 3 3 undefined 3 2 3 3 − √23 √ −1 √ √ 2 − undefined 2 2 1 −1 2 0 √ 3 √ − 2 −1 √ √ − √ 3 3 0 1 2 −2 √2 3 undefined 1 √ 3 1 √ 3 3 0 − √ 3 3 -1 √ − 3 undefined Other useful properties and identities: 2 tan θ 1 − tan2 θ ¯ ¯ r ¯ θ¯ ¯sin ¯ = 1 − cos θ ¯ 2¯ 2 r ¯ ¯ ¯ ¯ ¯cos θ ¯ = 1 + cos θ ¯ 2¯ 2 sin (−θ) = − sin (θ) tan (2θ) = cos (−θ) = cos (θ) tan (−θ) = − tan (θ) sin2 (θ) + cos2 (θ) = 1 tan2 (θ) + 1 = sec2 (θ) 1 + cot2 (θ) = csc2 (θ) tan θ 1 − cos θ sin θ = = 2 sin θ 1 + cos θ sin(θ + φ) = sin θ cos φ + cos θ sin φ 1 − cos θ 2 1 + cos θ cos2 θ = 2 sin2 θ = cos(θ + φ) = cos θ cos φ − sin θ sin φ tan θ + tan φ tan(θ + φ) = 1 − tan θ tan φ sin(θ − φ) = sin θ cos φ − cos θ sin φ cos(θ − φ) = cos θ cos φ + sin θ sin φ tan θ − tan φ tan(θ − φ) = 1 + tan θ tan φ sin θ cos φ = 1 [sin(θ + φ) + sin(θ − φ)] 2 1 [sin(θ + φ) − sin(θ − φ)] 2 1 cos θ cos φ = [cos(θ + φ) + cos(θ − φ)] 2 1 sin θ sin φ = [cos(θ − φ) − cos(θ + φ)] 2 cos θ sin φ = sin (2θ) = 2 sin (θ) cos (θ) cos (2θ) = cos2 (θ) − sin2 (θ) = 1 − 2 sin2 (θ) = 2 cos2 (θ) − 1 Inverse Trigonometric Functions Function Domain y = sin−1 x −1 ≤ x ≤ 1 y = cos−1 x −1 ≤ x ≤ 1 y = tan−1 x −∞ < x < ∞ y = cot−1 x −∞ < x < ∞ y = sec−1 x (−∞, −1] ∪ [1, ∞) y = csc−1 x (−∞, −1] ∪ [1, ∞) 2 Range − π2 ≤ y ≤ π 2 0≤y≤π − π2 < y < π 2 0<y<π £ £ ¢ £ ¢ 0, π2 ∪ π, 3π 2 ¢ ¡ ¤ − π2 , 0 ∪ 0, π2