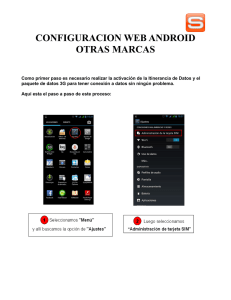
Abstracción de procedimientos

Abstracción de procedimientos
1.- Consideremos ABN (árboles binarios numéricos) sin nodos repetidos. Denimos los
siguientes conceptos:
Dados dos ABN, A y B, decimos que B es SUBARBOL PRINCIPAL de A si
B=A o B es un hijo de A, o B es subárbol principal de un hijo de A.
Todo nodo n de un árbol A es la raiz de un único subárbol principal de A que
llamaremos la DESCENDENCIA de n en A.
Dados dos nodos, n1 y n2, de un ABN A, decimos que n1 es PADRE de n2 en A
(o que n2 es DESCENDIENTE INMEDIATO de n1 en A), si n2 es raiz de uno
de los hijos de la descendencia de n1 en A. Decimos que n1 es ADYACENTE
a n2 en A si n1 es el padre de n2 en A o n2 es el padre de n1 en A.
Un nodo de la descendencia de n en A es un DESCENDIENTE de n en A.
Un CAMINO (de n1 a nm ) en un ABN, A, es una sucesión de nodos de A,
n1 , . . . , nm , tal que cada nodo es padre del siguiente en A.
Se pide:
1.
Dene un procedimiento intercambia que reciba como entrada un ABN, A, y
devuelva el ABN, obtenido intercambiando,en A, el hijo izquierdo con el hijo
derecho en todos los niveles.
2.
Dene un procedimiento es-nodo-de? que reciba como entrada un número n y
un ABN A y devuelva #t si n es nodo de A, y #f en caso contrario.
3.
Dene un procedimiento padre que reciba como entrada un número n y un
ABN A y devuelva el padre de n en A, si n es un nodo de A distinto de la raiz,
y #f en caso contrario.
4.
Dene un procedimeiento camino-hasta que reciba como entrada un número x
y un ABN A y devuelva la lista de los nodos que forman el camino desde la
raiz de A hasta x, si x es nodo de A, y #f si x no es nodo de A.
(dene a1 '((() 3 ()) 4 (() 1 ())))
(dene a4 '((((() 1 ()) 5 ()) 7 (() 3 (() 4 ()))) 6 ((() 10 ()) 8 ((() 9 ()) 11 (() 2
())))))
(intercambia a1 ) ->((() 1 ()) 4 (() 3 ()))
(intercambia a4 ) ->((((() 2 ()) 11 (() 9 ())) 8 (() 10 ())) 6 (((() 4 ()) 3 ()) 7 (() 5
(() 1 ()))))
1
(es-nodo-de? 4 a1 )
(es-nodo-de? 5 a1 )
(es-nodo-de? 13 a4 )
(es-nodo-de? 4 a4 )
(padre 3 a4 )
(padre 11 a4 )
(padre 6 a4 )
(padre 12 a4 )
(padre 3 a1 )
(camino-hasta 5 a4 )
(camino-hasta 2 a4 )
(camino-hasta 13 a4 )
(camino-hasta 11 a4 )
=>#t
=>#f
=>#f
=>#t
=>7
=>8
=>#f
=>#f
=>4
=>(6 7 5)
=>(6 8 11 2)
=>#f
=>(6 8 11)
2.- Dene un procedimiento, usando recursión terminal, multiplica que reciba como
entrada un predicado pred , un procedimiento de un argumento, f , y un número
entero positivo n , y devuelva como valor el producto de los elementos de la sucesión,
{f (k) : k = 0, . . . , n}, para los que k satisface el predicado pred .
(multiplica even? (lambda (x ) (∗ x x )) 5)
(multiplica odd? (lambda (x ) (∗ x x )) 5)
(multiplica (lambda (x ) (< 4 x 8)) (lambda (x ) x ) 10)
=>0
=>225
=>210
3.- Denir un procedimiento var-con-valor-maximo que reciba una función f de aridad
1 y un número natural n , y devuelva el menor elemento del intervalo [0, n] en el
que f alcanza su valor máximo en [0, n].
(var-con-valor-maximo sqrt 9)
(var-con-valor-maximo (lambda (x ) (− x )) 1e3)
(var-con-valor-maximo f 7)
=>9
=>0
=>4
donde f (n) = −n2 + 8n + 20.
4.- Dene un procedimiento parametrizado a-cada que reciba como entrada un predi-
cado pred y un procedimiento de un argumento proc , y devuelva como valor un
procedimiento que, al recibir como entrada una lista, l , devuelve la lista obtenida a
partir de l sustituyendo los elementos que satisfacen el predicado pred por el valor
obtenido al aplicarles el procedimiento proc .
((a-cada even? (lambda (x ) (+ x 1))) '(1 2 3 4 5 6))
((a-cada list? car ) '(2 (4 5) (a b c) j l))
((a-cada symbol? (lambda (x ) ())) '((2 3) (a f) g 3 h))
=>(1 3 3 5 5 7)
=>(2 4 a j l)
=>((2 3) (a f) () 3 ())
5.- Dene un procedimiento test que tome como argumentos un número natural n y un
predicado pred , y que devuelva un procedimiento denido por recursión terminal,
que reciba como entrada una lista l y devuelva #t, si al menos n elementos de l
verican el predicado pred , y #f en caso contrario.
((test 0 even? ) '())
((test 3 even? ) '(1 2 4 16 18))
((test 3 odd? ) '(1 2 4 16 18))
=>#t
=>#t
=>#f
2
6.- Denir un procedimiento sublistas que tome como argumento una lista l de números
no repetidos y ordenados en orden creciente, y que devuelva la lista de todas las
listas de números no repetidos y en orden creciente, cuyos elementos están en l (es
decir, la lista de todas las sublistas de l ).
(sublistas '())
(sublistas '(1 7 8))
(sublistas '(3 5))
=>(())
=>(() (1) (7) (8) (1 7) (1 8) (7 8) (1 7 8))
=>(() (3) (5) (3 5)))
7.- Denir el procedimiento suma-menor de forma que si recibe una lista de números
no repetidos, L y un número n , devuelva la lista formada por todas las sublistas de
L cuyos elementos suman un número menor o igual que n .
(suma-menor '(1 7 2 4) 9)
(suma-menor '(3 5 8 9 4) 2)
(suma-menor '(2 3 1 7) 6)
=>(() (4) (2) (2 4) (7) (7 2) (1) (1 4) (1 2)
(1 2 4) (1 7))
=>(())
=>(() (1) (3) (3 1) (2) (2 1) (2 3) (2 3 1))
8.- Denir un procedimiento min-prof que tome como argumento una lista numérica
(con al menos un número), y devuelva el mínimo de estos números.
(min-prof '((2) ((3 4) -1) (0 ((1)))))
(min-prof '(0 (0) ((0))))
(min-prof '((1 (-2)) 0 ((2) -1)))
=>−1
=>0
=>−2
9.- Se denomina cola de una lista l a una sublista de l formada por un elemento y los
siguientes. Por ejemplo, (3 4 5) es una cola de la lista (1 2 3 4 5). La lista vacía no
se considera una cola. Denir un procedimiento colas, que calcule las colas de una
lista dada.
(colas '())
=>()
(colas '(1 4))
=>((1 4) (4))
(colas '(1 4 5 2 3)) =>((1 4 5 2 3) (4 5 2 3) (5 2 3) (2 3) (3))
10.- Se denomina cabeza de una lista l a una sublista de l formada por el primer elemento
y los siguientes hasta uno dado. Por ejemplo, (1 2 3) es una cabeza de (1 2 3 4 5).
La lista vacía no se considera una cabeza. Denir un procedimiento cabezas , que
calcule las cabezas de una lista dada.
(cabezas '())
=>()
(cabezas '(1 4))
=>((1) (1 4))
(cabezas '(1 4 5 2 3)) =>((1) (1 4) (1 4 5) (1 4 5 2) (1 4 5 2 3))
11.- Utilizando el procedimiento cabezas , denir un procedimiento f-acumuladas que
calcule las frecuencias acumuladas de un conjunto de datos, cuyas frecuencias vienen
dadas en una lista.
(f-acumuladas '())
=>()
(f-acumuladas '(1 4))
=>(1 5)
(f-acumuladas '(1 4 5 2 3)) =>(1 5 10 12 15)
3
12.- Diremos que una matriz numérica n×n es un cuadrado mágico si cumple la siguiente
propiedad: las sumas de cada una de sus las, columnas y dos diagonales principales
coinciden. Por ejemplo:


2 9 4


 7 5 3 
6 1 8
es un cuadrado mágico, ya que todas sus las, columnas y diagonales principales
suman 15.
Representaremos una matriz numérica como una lista cuyos elementos son las las
del cuadrado, en forma de listas. Por ejemplo, el cuadrado anterior vendría representado por la siguiente lista: ((2 9 4) (7 5 3) (6 1 8)).
Se pide denir un procedimiento cuadrado-magico? que reciba una matriz numérica
(representada como hemos convenido) y compruebe si es o no un cuadrado mágico.
(cuadrado-magico? '((2 9 4) (7 5 3) (6 1 8)))
(cuadrado-magico? '((1 2 3) (4 5 6) (7 8 9)))
(cuadrado-magico? '((1 4) (3 4)))
=>#t
=>#f
=>#f
13.- Denir un procedimiento, usando recursión terminal, prod-arb , que tome un número arbitrario de argumentos y devuelva como valor el producto de los elementos de
entrada que sean números. Si no hay ningún número entre los argumentos recibidos
devuelve como valor 1. Por ejemplo:
(prod-arb 'a 'hola 7 'adios 2)
(prod-arb '(3 4) 'adios '())
(prod-arb '(100 a) 'hola 2 'adios 3 5)
=>14
=>1
=>30
14.- Dene un procedimiento, usando recursión terminal, suma-pos que reciba un
número arbitrario de argumentos que sean números y devuelva la suma de cada uno
de dichos números elevado a la posición que ocupa (empezando en 1).
(suma-pos )
(suma-pos 1 0 1 0 1 1)
(suma-pos 2 3 0 1)
=>0
=>4
=>12
15.- Se dice que un conjunto de números naturales (distintos) x0 , . . . , xn está ordenado
cíclicamente si existe un índice i tal que la sucesión xi , xi+1 , . . . , xn , x0 , . . . , xi−1 está
ordenada (en orden creciente). Denir un procedimiento ordenado-cic? que reciba un
número arbitrario de números, y devuelva el índice a partir del cual están ordenados,
si el conjunto de números está ordenado cíclicamente y #f en caso contrario.
(ordenado-cic? 1 2 3 4)
(ordenado-cic? 4 6 7 5 4 3)
(ordenado-cic? 5 8 2 3)
=>0
=>#f
=>2
4
16.- Denir un procedimiento parametrizado argumento-ref , que tome como argumento
un número entero, i , y devuelva como valor un procedimiento, con un número arbitrario de argumentos, que devuelve como valor su i -ésimo argumento, si existe, y
produce un error en caso contrario.
((argumento-ref 3) 'a 'hola 'adios)
((argumento-ref 2) 32 '(3 4) 'adios 23 '())
((argumento-ref 5) 'a 'hola 'adios)
=>adios
=>(3 4)
=>argumento-ref: indice-incorrecto
17.- Denir un procedimiento sumapred que tome como argumento un predicado pred
y devuelva un procedimiento que admita un número variable de argumentos x1 ,
P
. . . ,xn , y devuelva ni=1 yi donde yi = x2i si xi cumple el predicado pred , e yi = xi
en caso contrario.
((sumapred odd? ) 2 4 3 5)
=>40
((sumapred integer? ) 1 1.5 2 2.5 3 3.5 4) =>37.5
((sumapred zero? ))
=>0
18.- Dene un procedimiento parametrizado grafo que reciba como entrada un predicado
pred y un procedimiento de un argumento proc , y devuelva como valor un procedimiento con un número arbitrario de parámetros, que devuelve la lista formada
por los pares punteados cuyos primeros elementos son los elementos recibidos que
satisfacen pred y sus segundos elementos son los valores obtenidos al aplicar a dichos
elementos el procedimiento proc .
((grafo even? (lambda (x ) (+ x 1))) 1 2 3 4 5)
=>((4 . 5) (2 . 3))
((grafo list? car ) 2 '(4 5) '(a b c) 'j 'l)
=>(((a b c) . a) ((4 5) . 4))
((grafo symbol? (lambda (x ) #t)) '(2 3) '(a f) 'm 'g 3 'h)
=>((h . #t) (g . #t) (m . #t))
19.- Dene un procedimiento, usando recursión terminal, suma-numeros que reciba
como entrada un número arbitrario de listas y devuelva como valor la suma de los
elementos de nivel superior de las listas recibidas, que sean números. Por ejemplo:
(suma-numeros '(hola 3 adios) '(hola 2 de 3 nuevo))
(suma-numeros '((3) (2 3)) '(a b c (d) (8 (9))))
(suma-numeros '(1 2 3) '(3 (1 1 1 1) 6) '(2 3) '(1) '())
=>8
=>0
=>21
20.- Consideremos el siguiente procedimiento foldr , donde proc será un procedimiento
de aridad dos:
(dene foldr
(lambda (proc a )
(letrec ((aux (lambda (ls )
(if (null? ls )
a
(proc (car ls ) (aux (cdr ls )))))))
aux )))
5
Denir, usando foldr , los siguientes procedimientos:
Un procedimiento inversa que tome como argumento una lista l y devuelva
como valor una lista con los mismos elementos de l en orden inverso.
Un procedimiento composicion que tome como entrada una lista de procedimientos (todos de un sólo argumento) y devuelva como valor el procedimiento
que se obtiene al componerlos.
Un procedimiento suma , que devuelva la suma de los elementos de una lista
numérica.
Un procedimiento producto , que devuelva el producto de los elementos de una
lista numérica.
Un procedimiento conjuncion , que, aplicado a una lista, actúe como and con
sus elementos.
Un procedimiento disyuncion , que, aplicado a una lista, actúe como or con sus
elementos.
21.- Consideremos el siguiente procedimiento:
(dene patron
(lambda (f g )
(letrec ((aux (lambda (ls )
aux )))
(apply f (map g ls )))))
Denir, usando patron , un procedimiento longitud , que tome como argumento una
lista l y devuelva como valor el número de elementos de l .
22.- Denir un procedimiento patron-suma que tome como argumento una función f , y
devuelva como valor un procedimiento que reciba dos números a , b y una función
proximo , y que devuelva el valor de
b
X
f (k)
k=a
donde k va tomando valores según la función proximo .
Usar patron-suma para denir los siguientes procedimientos:
suma-cubos , que efectúe la suma de los cubos de los números naturales comprendidos entre dos dados.
aprox-e , que devuelva una aproximación del número e, que se ha obtenido
sumando la serie que dene a e desde 0 hasta n.
integral-denida , que calcule la integral de f entre los límites a y b, usando la
fórmula:
Z b
a
f = [f (a +
dx
dx
dx
) + f (a +
+ dx) + f (a +
+ 2dx) + . . .]dx
2
2
2
6
23.- Pretendemos denir un procedimiento que codique mensajes tales como
((e l ) (a t a q u e ) (a ) (l a s ) (8 p m ))
del siguiente modo:
(a) Contamos las letras de cada palabra: llp =(2 6 1 3 3)
(b) Eliminamos los paréntesis: (e l a t a q u e a l a s 8 p m )
(c) Reagrupamos de 4 en 4 letras, dejando el último grupo con el resto:
((e l a t ) (a q u e ) (a l a s ) (8 p m ))
(d) Invertimos cada grupo: ((t a l e ) (e u q a ) (s a l a ) (m p 8))
(e) Eliminamos los paréntesis de nuevo: (t a l e e u q a s a l a m p 8)
(f) Finalmente, reagrupamos tal como indique la lista llp invertida:
((t a l ) (e e u ) (q ) (a s a l a m ) (p 8))
obteniendo así el mensaje codicado.
Se pide:
(1) Denir un procedimiento g4 que resuelva el paso (c) anterior, esto es:
(g4 '(e l a t a q u e a l a s 8 p m)) =>((e l a t) (a q u e) (a l a s) (8 p m))
(2) Denir un procedimiento agrupa que resuelva el paso (f) anterior, esto es, que
tome una lista de letras y otra de números (cuya suma coincida con el número
total de letras) y agrupe las letras tal como indican los números. Por ejemplo:
(agrupa '(t a l e e u q a s a l a m p 8) '(3 3 1 6 2))
=>((t a l) (e e u) (q) (a s a l a m) (p 8))
(3) Denir un procedimiento clave que realice el proceso completo. Por ejemplo:
(clave '((e l) (a t a q u e) (a) (l a s) (8 p m)))
=>((t a l) (e e u) (q) (a s a l a m) (p 8))
24.- Denir el procedimiento nota-nal que recibe cuatro variables, p1 , p2 , p3 y p4 (son
los pesos asignados a cuatro ejercicios), y devuelve un procedimiento que recibe una
lista l , cuyos elementos son listas de cuatro elementos (las notas de exámenes de
cuatro ejercicios (e1 e2 e3 e4 )), y devuelve una lista con la nota nal de cada
examen, obtenida con la fórmula
(p1 ∗ e1) + (p2 ∗ e2) + (p3 ∗ e3) + (p4 ∗ e4)
((nota-nal 0.2 0.1 0.5 0.2) '((3 6 7 2) (4 5 6 8) (0 9 5 1) (9 6 5 1)))
=>(5.1 5.9 3.6 5.1)
((nota-nal 0.2 0.1 0.5 0.2) '((3 6 7 2) (8 8 8 8) (0 9 5 1) (10 10 10 10)))
=>(5.1 8.0 3.6 10.0)
7
25.- 1. Denir un procedimiento agrupa-segun-criterio que reciba un predicado pred ,
y devuelva un procedimiento que reciba una lista l y devuelva una lista con
dos elementos: el primero, la lista de elementos de l que verican el predicado,
y el segundo la lista de los que no lo verican.
((agrupa-segun-criterio even? ) '(1 2 3 4 5 6 7)) =>((2 4 6) (1 3 5 7))
((agrupa-segun-criterio odd? ) '(1 2 3 4 5 6 7)) =>((1 3 5 7) (2 4 6))
((agrupa-segun-criterio zero? ) '(1 2 3 4 5 6 7)) =>(() (1 2 3 4 5 6 7))
2.
Usando el apartado anterior, denir un procedimiento agrupa-numeros que
reciba una lista l , y devuelva una lista cuyos elementos sean dos listas: el
primero la lista de los números de l , y la segunda con los demás elementos.
26.- 1. Denir un procedimiento agrupa-segun-tamaño que reciba un número natural
n , y devuelva un procedimiento que recibe una lista l , y devuelve una lista con
los mismos elementos que l , agrupados en listas de n elementos.
((agrupa-segun-tamaño 3) '(q w e 4 r t 5 y 6 u))
=>((q w e) (4 r t) (5 y 6) (u))
((agrupa-segun-tamaño 5) '(q w e 4 r t 5 y 6 u e r t))
=>((q w e 4 r) (t 5 y 6 u) (e r t))
2.
Denir el procedimiento g4 del ejercicio 23.
27.- Tenemos varias urnas. Cada urna contiene un número de objetos de una determi-
nada forma, color y tamaño. Representamos el conjunto de urnas como una lista de
sublistas. Cada sublista representa a una urna. Ejemplo:
(dene lista-urnas
'((circulo rojo grande 7) (cuadrado verde grande 2)
(triangulo verde mediano 3) (cuadrado rojo pequeño 5)
(circulo verde grande 5)))
1.
Escribir un procedimiento selecciona-por-atributos , que recibiendo una lista de
urnas, devuelva un procedimiento que recibiendo un número indeterminado de
atributos, devuelva la lista de todas las urnas que contengan objetos con todos
esos atributos.
((selecciona-por-atributos lista-urnas ) 'circulo 'grande)
=>((circulo rojo grande 7) (circulo verde grande 5))
((selecciona-por-atributos lista-urnas ) 'cuadrado 'rojo)
=>((cuadrado rojo pequeño 5))
2.
Escribir el procedimiento cuenta-cuantos , que recibiendo una lista de urnas,
devuelva un procedimiento que recibiendo un número indeterminado de atributos, devuelva el número total de objetos que, repartidos entre todas las urnas,
tienen todos esos atributos.
((cuenta-cuantos lista-urnas ) 'circulo 'grande)
=>12
((cuenta-cuantos lista-urnas ) 'verde)
=>10
((cuenta-cuantos lista-urnas ) 'cuadrado 'mediano) =>0
8
28.- (a) Denir un procedimiento, no recursivo (usando map y apply), suma-abs-lista-
dif que reciba dos listas numéricas, l1 y l2 , de igual longitud, y devuelva la
suma de las diferencias en valor absoluto de los elementos de l1 y l2 . Por
ejemplo:
(suma-abs-lista-dif '(2 3 4 5) '(3 2 1 4))
=>|2 − 3| + |3 − 2| + |4 − 1| + |5 − 4| = 6
(suma-abs-lista-dif '(0 1 0 1 0 1) '(1 0 1 0 1 0))
=>|0 − 1| + |1 − 0| + |0 − 1| + |1 − 0| + |0 − 1| + |1 − 0| = 6
(b) Denir un procedimiento, no recursivo (usando map y apply), suma-pos-listadif que reciba dos listas numéricas, l1 y l2 , de igual longitud, y devuelva la
suma de las diferencias de los elementos de l1 y l2 que sean positivas. Por
ejemplo:
(suma-pos-lista-dif '(2 3 4 5) '(3 2 1 4))
=>(3 − 2) + (4 − 1) + (5 − 4) = 5
(suma-pos-lista-dif '(0 1 0 1 0 1) '(1 0 1 0 1 0))
=>(1 − 0) + (1 − 0) + (1 − 0) = 3
(c) Denir un procedimiento, no recursivo (usando map y apply), suma-neg-listadif que reciba dos listas numéricas, l1 y l2 , de igual longitud, y devuelva el
valor absoluto de la suma de las diferencias de los elementos de l1 y l2 que
sean negativas. Por ejemplo:
(suma-neg-lista-dif '(2 3 4 5) '(3 2 1 4))
=>|(2 − 3)| = 1
(suma-neg-lista-dif '(0 1 0 1 0 1) '(1 0 1 0 1 0))
=>|(0 − 1) + (0 − 1) + (0 − 1)| = 3
29.- (a) Denir un procedimiento parametrizado, no recursivo (usando map y apply ),
elimina-ocurrencias , que reciba un dato, x , y devuelva un procedimiento que
al recibir una lista, l , devuelva la lista resultante de eliminar en l todos los
elementos de primer nivel iguales a x . Por ejemplo:
((elimina-ocurrencias 1) '(1 2 (1) 2 1))
((elimina-ocurrencias 'dato) '(((dato) dato) toda (((toda)))))
=>(((dato) dato) toda (((toda))))
=>(2 (1) 2)
(b) Denir un procedimiento, no recursivo (usando map y apply ), minima-distancia ,
usando el procedimiento anterior, que reciba como argumentos una lista de
puntos del plano, representados como listas de dos elementos, y devuelva la
mínima distancia existente entre cualesquiera dos puntos de dicha lista. Por
ejemplo:
(minima-distancia '((0 0) (0 1) (1 0) (1 1)))
(minima-distancia '((3 2) (4 7) (11 0)))
9
=>1.0 [= dist((0 0), (0 1))]
=>5.099019 [= dist((3 2), (4 7))]