Tipos de matrices

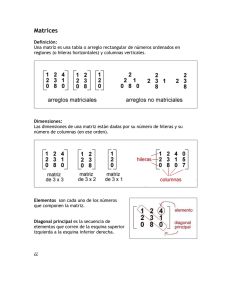
Taller de matrices
Tipos de matrices
Una matríz puede ser clasificada por tipos, es posible que para una matriz en
particular pertenezca a más de un tipo.
 Matríz fila: es una matríz con solamente una fila
Ejemplo 7
4 matríz fila de orden 1x1
9
2 5 matríz fila de orden 1x3
 Matríz columna: es una matríz con solamente una columna
Ejemplo 8:
3 es una matriz columna de orden 1x1
5
es una matríz columna de orden 2x1
3
Una matríz columna de orden 2x1 es también llamada vector matriz
 Matriz cero o matríz nula: es una matriz en la cual todos sus
elementos son ceros
Ejemplo 9:
0 0 0
, A es una matríz cero (o nula) de orden 2x3
0 0 0 Profesor Sr. Christian Cortés D.
Sesión N° 4
Taller de matrices
 Matríz cuadrada: es una matríz en la cual el número de filas es igual al
número de columnas.
Ejemplo 10:
6 3 , T es una matriz cuadrada 2x2, o bien decimos que T es una
0 4
matriz cuadrada de orden 2
7 1 9 3 2 5 V es una matriz cuadrada 3x3, o bien decimos que V es
2 1 8 una matriz cuadrada de orden 3
 Matríz diagonal: es una matriz cuadrada en la cual todos los elementos
son cero con la excepción de aquellos ubicados en la diagonal desde la
parte superior izquierda a la parte derecha inferior esta diagonal recibe
el nombre de diagonal principal de la matríz
Ejemplo 11:
3 0 0 0 8 0 , B es una matríz diagonal
0 0 2
 Matríz unidad: llamada también identidad, es una matriz diagonal
cuyos elementos de la diagonal son todos 1.
Ejemplo 12:
1 0 0 0 1 0
0 0 1
es una matriz unidad o es la identidad de las matrices
cuadradas de orden 3 también llamada
Profesor Sr. Christian Cortés D.
Sesión N° 4
Taller de matrices
 Matríz escalar: Es una matriz diagonal
, con todos los
elementos de la diagonal iguales, es decir:
0 Ejemplo 13:
Ejemplo 14:
7 0
0 7
2 0 0
0 2 0
0 0 2
 Matríz traspuesta: Dada una matriz A, se llama traspuesta de A y
simbolizada por
a la matriz que se obtiene intercambiando filas por
columnas, así la primera fila de A corresponde a la primera columna de
y así sucesivamente es decir si
entonces
definición también se deduce que si A es de orden
. De la
, entonces
es
de orden
Ejemplo 15:
Sí
1 5
entonces
2 6
1 2
5 6
De esta definición se puede concluir que:
 Matríz simétrica: Una matriz cuadrada es simétrica si
si
,
Ejemplo 16:
La matriz
2 5
es una matriz simétrica ya que
5 2
Profesor Sr. Christian Cortés D.
Sesión N° 4
, es decir
Taller de matrices
 Matriz triangular superior: es una matriz cuadrada en la cual todos
los elementos que están bajo la diagonal principal son 0 (ceros)
Ejemplo 17:
La matriz
5 2 3 1
0 1 3 2
es una matriz triangular superior
0 0 5 1
0 0 0 3  Matriz triangular inferior: es una matriz cuadrada en la cual todos los
elementos que están sobre la diagonal principal son 0 (ceros)
Ejemplo 18:
La matriz
5 0 0 0
3 1 0 0
es una matriz triangular inferior
3 2 6 0
1 4 5 9
 Matriz triangular: es una matriz cuadrada que es triangular superior e
inferior a la vez.
Ejemplo 19:
La matríz
1 0 0 0 0
0 1 0 0 0 0 0 1 0 0 0 0 0 1 0
Profesor Sr. Christian Cortés D.
Sesión N° 4